BIOPHYSICS LABORATORY
MIDTERM NOTES AND SAMPLE QUESTIONS
EXPERIMENT 1: THE VERNIER AND MICROMETER CALIPER
OBJECTIVES
TO KNOW HOW TO DETERMINE THE LEAST COUNT OF THE CALIPER USED AND
TO LEARN HOW TO USE THE VERNIER AND MICROMETER CALIPERS CORRECTLY
APPARATUS
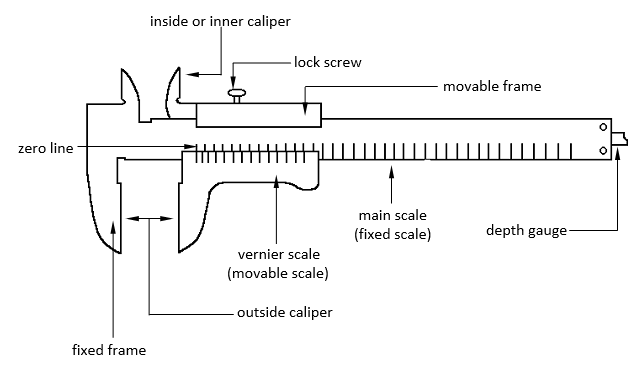
VERNIER CALIPER
MICROMETER CALIPER
CYLINDER
BEAM BALANCE
SPHERE
CUBE
WASHER
VERNIER CALIPER
AN AUXILIARY SLIDING SCALE WHICH ENABLES ONE TO INCREASE HIS ACCURACY IN MEASUREMENT.
FORMULA:
Total Measurement = Main Scale Reading + (Sequential Vernier Scale Marking × Least Count)
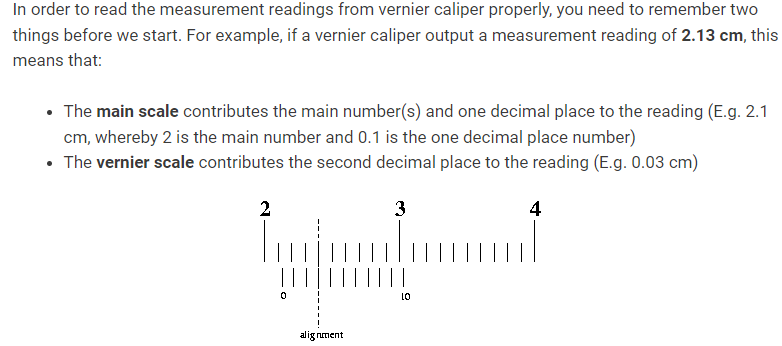
EXAMPLE 1:
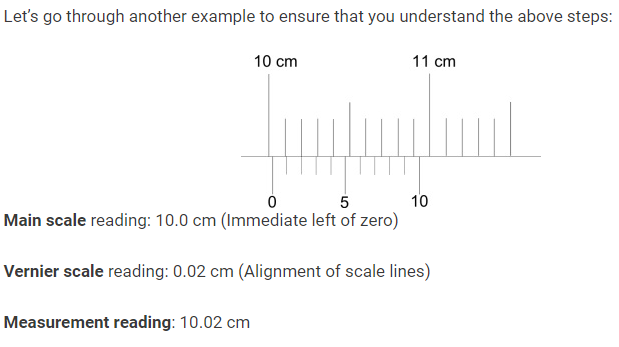
EXAMPLE 2:

MICROMETER CALIPER
PRECISE MEASUREMENT OF SMALL LENGTHS AND DIAMETERS.
FOR EVERY ONE REVOLUTION(5O divisions) OF THE SCREW, THE JAW ADVANCES HALF A MILLIMETER.

FORMULA:
Total Measurement = Main Scale Reading + (Sequential Micrometer Scale Marking × Least Count)

Other formulas
note: diameter=r/2
DENSITY=mass(g)/volume (cm³)
CUBE= S³
CYLINDER=πr²h
SPHERE: 4/3πr³
WASHER: πrout²-rin²)t

PRACTICE QUESTIONS WITH ANSWERS
1. What is the typical least count (smallest measurable value) of a Vernier Caliper?
A) 0.1 mm
B) 0.01 mm
C) 0.02 mm
D) 0.5 mm
Answer: C) 0.02 mm
2. How many divisions are usually present on the Vernier scale of a Vernier Caliper?
A) 10
B) 20
C) 50
D) 100
Answer: B) 20
3. What is the typical least count of a Micrometer Caliper?
A) 0.1 mm
B) 0.01 mm
C) 0.02 mm
D) 0.001 mm
Answer: B) 0.01 mm
4. Which part of the Vernier Caliper is used to measure the internal diameter of objects?
A) Main scale
B) Vernier scale
C) Lower jaws
D) Upper jaws
Answer: D) Upper jaws
5. What is the main advantage of using a Micrometer Caliper over a Vernier Caliper?
A) Measures larger objects
B) Easier to use
C) More accurate for smaller dimensions
D) Can measure both internal and external dimensions
Answer: C) More accurate for smaller dimensions
6. When using a Vernier Caliper, how do you determine the measurement?
A) Subtract the Vernier reading from the main scale
B) Add the Vernier reading to the main scale
C) Multiply the Vernier reading by the least count
D) Divide the Vernier reading by the least count
Answer: B) Add the Vernier reading to the main scale
7. The pitch of a screw in a Micrometer Caliper represents:
A) The number of divisions on the sleeve
B) The distance the spindle moves per full rotation of the thimble
C) The smallest reading on the thimble
D) The length of the thimble
Answer: B) The distance the spindle moves per full rotation of the thimble
8. How is zero error in a Vernier Caliper checked?
A) By closing the jaws completely and checking the alignment of the zero mark on the Vernier scale with the zero on the main scale
B) By rotating the Vernier scale
C) By measuring a standard object
D) By adjusting the main scale
Answer: A) By closing the jaws completely and checking the alignment of the zero mark on the Vernier scale with the zero on the main scale
9. What should be done if a negative zero error is found in a Micrometer Caliper reading?
A) Add the error value to the measured value
B) Subtract the error value from the measured value
C) Multiply the measured value by the error
D) Ignore the error
Answer: A) Add the error value to the measured value
10. What is the purpose of the ratchet stop on a Micrometer Caliper?
A) To ensure accurate measurement by applying consistent pressure
B) To lock the spindle in place
C) To adjust the zero reading
D) To reset the scale to zero
Answer: A) To ensure accurate measurement by applying consistent pressure
11. A Vernier Caliper has a main scale reading of 7.5 cm, and the 9th Vernier division coincides with the main scale. The least count is 0.02 cm. What is the total reading?
Solution:
Total reading = Main scale reading + (Vernier scale division × Least count)
Main scale reading = 7.5 cm
Vernier division = 9
Least count = 0.02 cm
Total reading = 7.5 cm + (9 × 0.02 cm)
Total reading = 7.5 cm + 0.18 cm
Total reading = 7.68 cm
Answer: 7.68 cm
14. A student uses a Vernier Caliper where the main scale division is 1 mm and 20 Vernier scale divisions match 19 mm on the main scale. Calculate the least count of the Vernier Caliper.
Solution:
Least count = (Value of 1 main scale division) ÷ (Number of Vernier scale divisions)
Main scale division = 1 mm
20 Vernier scale divisions = 19 mm (given)
Least count = (19 mm ÷ 20)
Least count = 0.95 mm
Now, subtract from 1 main scale division to get the least count:
Least count = 1 mm - 0.95 mm
Least count = 0.05 mm
Answer: 0.05 mm
15. A Micrometer Caliper shows a reading of 10 mm on the sleeve and 23 divisions on the thimble scale. The least count is 0.01 mm. If the instrument has a negative zero error of 0.02 mm, what is the correct measurement?
Solution:
Total reading = Main scale reading + (Thimble reading × Least count)
Main scale reading = 10 mm
Thimble reading = 23
Least count = 0.01 mm
Zero error = -0.02 mm (negative zero error)
Total reading = 10 mm + (23 × 0.01 mm)
Total reading = 10 mm + 0.23 mm
Total reading = 10.23 mm
Correct reading = Total reading - Zero error
Correct reading = 10.23 mm - (-0.02 mm)
Correct reading = 10.25 mm
Answer: 10.25 mm
EXPERIMENT 2: RESULTANT VECTORS
OBJECTIVES
TO STUDY AND CHECK EXPERIMENTALLY THE GRAPHICAL AND ANALYTICAL METHODS OF DETERMINING THE RESULTANT OF THE GIVEN VECTORS
APPARATUS
FORCE TABLE
WEIGHT HANGERS
SET OF SLOTTED MASSES
RULER
PROTRACTOR
FORMULAS

PRACTICE QUESTIONS WITH ANSWERS
1. What is a resultant vector?
A) A vector that represents the sum of two or more vectors.
B) A vector that is always perpendicular to other vectors.
C) A vector that represents the difference between two vectors.
D) A vector with zero magnitude.
Answer: A) A vector that represents the sum of two or more vectors.
2. When two vectors are added and their resultant is zero, the vectors are said to be:
A) Parallel
B) Anti-parallel
C) Equal in magnitude but opposite in direction
D) At right angles
Answer: C) Equal in magnitude but opposite in direction
3. If two vectors of equal magnitude are at a 90° angle to each other, what is the magnitude of their resultant?
A) Equal to the magnitude of one of the vectors
B) Twice the magnitude of one of the vectors
C) √2 times the magnitude of one of the vectors
D) Half the magnitude of one of the vectors
Answer: C) √2 times the magnitude of one of the vectors
4. What is the direction of the resultant vector when two vectors are added?
A) It is always horizontal
B) It depends on the magnitudes and directions of the vectors
C) It is always vertical
D) It is always along one of the original vectors
Answer: B) It depends on the magnitudes and directions of the vectors
5. Which law is typically used to find the magnitude of the resultant of two vectors when their magnitudes and the angle between them are known?
A) Law of Sines
B) Law of Cosines
C) Pythagorean Theorem
D) Newton's First Law
Answer: B) Law of Cosines
6. The resultant of two vectors can be found by placing the vectors:
A) Tip-to-tail
B) Tail-to-tail
C) Parallel to each other
D) Head-to-head
Answer: A) Tip-to-tail
7. If two vectors A⃗ and B⃗ are added using the parallelogram method, the diagonal of the parallelogram represents:
A) The vector sum
B) The difference of the vectors
C) The scalar product of the vectors
D) A unit vector
Answer: A) The vector sum
8. Which of the following is NOT true about the magnitude of the resultant vector?
A) It is always larger than the magnitude of each individual vector
B) It is the maximum when two vectors are in the same direction
C) It is the minimum when two vectors are in opposite directions
D) It depends on the angle between the vectors
Answer: A) It is always larger than the magnitude of each individual vector
9. When two vectors are at an angle of 180° to each other, the resultant vector is:
A) Zero
B) Equal to the sum of the two vectors
C) Equal to the difference of the two vectors
D) Twice the magnitude of one of the vectors
Answer: C) Equal to the difference of the two vectors
10. The magnitude of the resultant vector of two perpendicular vectors A⃗ and B⃗ is found by:
A) Adding their magnitudes directly
B) Subtracting their magnitudes
C) Using the Pythagorean theorem
D) Multiplying their magnitudes
Answer: C) Using the Pythagorean theorem

EXPERIMENT 3: UNIFORM SPEED
OBJECTIVES
IN THIS ACTIVITY, THE MOVING OBJECT IS A STEEL BALL AND THE MEDIUM IS OIL WITHIN A GLASS TUBE
WE WISH TO VERIFY THE RELATIONSHIP OF DISTANCE VS. TIME FOR THE METAL BALL MOVING AT A CONSTANT SPEED BY GRAPHICAL ANALYSIS
APPARATUS
SLOW BALL APPARATUS AND MILLESECONDS TIMER
FORMULAS

PRACTICE QUESTIONS WITH ANSWERS
1. What is uniform speed?
A) Speed that changes over time.
B) Speed that increases uniformly over time.
C) Speed that decreases uniformly over time.
D) Speed that remains constant over time.
Answer: D) Speed that remains constant over time.
2. Which of the following is true about an object moving with uniform speed?
A) The object’s velocity is changing.
B) The object covers equal distances in unequal intervals of time.
C) The object covers equal distances in equal intervals of time.
D) The object accelerates at a constant rate.
Answer: C) The object covers equal distances in equal intervals of time.
3. A car moving at a uniform speed covers a distance of 60 km in 1 hour. How far will it travel in 3 hours?
A) 120 km
B) 180 km
C) 200 km
D) 240 km
Answer: B) 180 km
4. If an object is moving with uniform speed, its acceleration is:
A) Zero
B) Constant and non-zero
C) Increasing
D) Decreasing
Answer: A) Zero
5. The distance-time graph of an object moving with uniform speed is:
A) A curved line
B) A straight horizontal line
C) A straight sloping line
D) A vertical line
Answer: C) A straight sloping line
6. An object moving at a uniform speed of 10 m/s travels a distance of 100 meters. How much time does it take?
A) 5 seconds
B) 10 seconds
C) 15 seconds
D) 20 seconds
Answer: B) 10 seconds
7. In a uniform speed experiment, the key equipment used to measure the time taken is:
A) Speedometer
B) Stopwatch
C) Thermometer
D) Ammeter
Answer: B) Stopwatch
8. An object travels 50 meters in 5 seconds with uniform speed. What is its speed?
A) 5 m/s
B) 8 m/s
C) 10 m/s
D) 15 m/s
Answer: C) 10 m/s
9. Which of the following scenarios describes motion at uniform speed?
A) A car speeding up on the highway.
B) A cyclist moving at a steady pace on a flat road.
C) A rocket accelerating into space.
D) A ball falling freely under gravity.
Answer: B) A cyclist moving at a steady pace on a flat road.
10. In a uniform speed experiment, what should be observed if the object is truly moving at a uniform speed?
A) Increasing speed readings over time.
B) Decreasing speed readings over time.
C) Constant speed readings at regular time intervals.
D) Speed readings fluctuating at random intervals.
Answer: C) Constant speed readings at regular time intervals.
EXPERIMENT 4: UNIFORM ACCELERATION ON AN INCLINED PLANE
OBJECTIVES
TO DETERMINE THE ACCELERATION BY GRAPHICAL AND THEORETICAL ANALYSIS
APPARATUS
LINEAR AIR TRACK SET UP
MILLISECONDS TIMER
FORMULAS
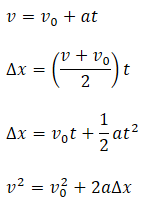
PRACTICE QUESTIONS WITH ANSWERS
1. What is uniform acceleration?
A) Acceleration that changes over time.
B) Acceleration that remains constant over time.
C) Acceleration that increases with distance.
D) Acceleration that decreases over time.
Answer: B) Acceleration that remains constant over time.
2. When an object moves down an inclined plane with uniform acceleration, the net force acting on it is:
A) Zero
B) Constant and directed along the incline
C) Increasing
D) Decreasing
Answer: B) Constant and directed along the incline
3. In the experiment of uniform acceleration on an inclined plane, which physical quantity changes uniformly?
A) Distance
B) Speed
C) Time
D) Mass
Answer: B) Speed
4. Which of the following graphs represents uniform acceleration on an inclined plane?
A) A straight line on a distance-time graph
B) A straight line on a velocity-time graph
C) A horizontal line on an acceleration-time graph
D) A curved line on a distance-time graph
Answer: D) A curved line on a distance-time graph
5. What factor affects the acceleration of an object on an inclined plane?
A) The mass of the object
B) The length of the inclined plane
C) The angle of inclination of the plane
D) The color of the object
Answer: C) The angle of inclination of the plane
6. If an object is released from rest on an inclined plane with uniform acceleration, what will be its velocity after 4 seconds if the acceleration is 2 m/s²?
A) 2 m/s
B) 4 m/s
C) 6 m/s
D) 8 m/s
Answer: D) 8 m/s
7. The acceleration due to gravity on an inclined plane is given by gsinθ. What does θ represent?
A) The speed of the object
B) The angle of inclination of the plane
C) The height of the plane
D) The time taken by the object to reach the bottom
Answer: B) The angle of inclination of the plane
8. In an experiment, a cart moves down an inclined plane with uniform acceleration. If the acceleration is doubled, what will happen to the velocity of the cart at any given time?
A) It will be halved.
B) It will double.
C) It will remain the same.
D) It will quadruple.
Answer: B) It will double.
9. What is the shape of the velocity-time graph for an object moving down an inclined plane with uniform acceleration?
A) Curved
B) Horizontal line
C) Straight sloping line
D) Vertical line
Answer: C) Straight sloping line
10. In a uniform acceleration experiment on an inclined plane, what apparatus is typically used to measure the time intervals?
A) Meter stick
B) Stopwatch
C) Spring balance
D) Thermometer
Answer: B) Stopwatch


EXPERIMENT 5: FREE FALL ACCELERATION
OBJECTIVES
IN THIS ACTIVITY, YOU ARE TO CALCULATE THE VALUE Of g BY MEASURING THE TIMES, t, TAKEN TO FALL VARIOUS DISTANCES, D.
APPARATUS
FREE FALL APPARATUS
FORMULAS
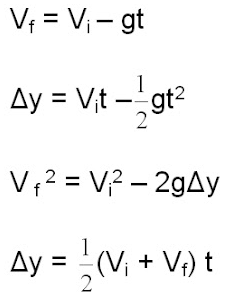
SAMPLE QUESTIONS WITH ANSWERS
1. What type of motion does an object in free fall exhibit?
A) Uniform motion
B) Uniformly accelerated motion
C) Non-uniform motion
D) Circular motion
Answer: B) Uniformly accelerated motion
2. What is the value of acceleration due to gravity at sea level?
A) 9.8 m/s²
B) 10 m/s²
C) 9.81 m/s²
D) 11 m/s²
Answer: A) 9.8 m/s²
3. If a rock is dropped from a height of 45 meters, how long will it take to hit the ground? (Use g=9.8m/s2)
A) 2.0 seconds
B) 3.0 seconds
C) 4.0 seconds
D) 5.0 seconds
Answer: B) 3.0 seconds
4. When an object is thrown upwards, at what point is its velocity zero?
A) At the moment of release
B) At the maximum height
C) Just before hitting the ground
D) At halfway up its trajectory
Answer: B) At the maximum height
5. A parachutist jumps from a plane and reaches terminal velocity. What happens to the net force acting on the parachutist?
A) It increases
B) It decreases
C) It becomes zero
D) It changes direction
Answer: C) It becomes zero
6. What happens to the speed of an object in free fall as it falls for a longer time?
A) The speed remains constant.
B) The speed increases.
C) The speed decreases.
D) The speed fluctuates.
Answer: B) The speed increases.
7. If an object is thrown vertically downward with an initial velocity of 5 m/s, what is its velocity after 2 seconds? (Use g=9.8m/s2)
A) 9.8 m/s
B) 14.6 m/s
C) 5 m/s
D) 19.6 m/s
Answer: B) 14.6 m/s
8. In free fall, what force acts on an object when it is in motion?
A) Normal force
B) Gravitational force
C) Frictional force
D) Tension force
Answer: B) Gravitational force
9. How does air resistance affect free-falling objects?
A) It has no effect.
B) It increases their acceleration.
C) It decreases their acceleration.
D) It makes them fall faster.
Answer: C) It decreases their acceleration.
10. What is the relationship between the mass of an object and its free fall acceleration?
A) Heavier objects fall faster.
B) Lighter objects fall faster.
C) All objects fall with the same acceleration regardless of mass.
D) Mass has no effect on free fall.
Answer: C) All objects fall with the same acceleration regardless of mass.

EXPERIMENT 6: FORCE AND ACCELERATION
OBJECTIVES
TO DETERMINE BY GRAPHICAL ANALYSIS THE RELATIONSHIP BETWEEN THE FORCE AND THE ACCELERATION OF AN OBJECT WITH CONSTANT MASS
APPARATUS
LINEAR AIR TRACK SET UP
SET OF MASSES
MILLISECONDS TIMER
FORMULAS

SAMPLE QUESTIONS WITH ANSWERS
1. According to Newton's second law of motion, which equation correctly relates force, mass, and acceleration?
A) F=m+aF = m + aF=m+a
B) F=maF = maF=ma
C) F=m/aF = m/aF=m/a
D) F=a/mF = a/mF=a/m
Answer: B) F=maF = maF=ma
2. If a 5 kg object experiences a net force of 20 N, what is its acceleration?
A) 2 m/s²
B) 4 m/s²
C) 5 m/s²
D) 10 m/s²
Answer: B) 4 m/s²
3. Which of the following correctly defines weight?
A) The force of gravity acting on an object.
B) The mass of an object.
C) The resistance to motion.
D) The acceleration of an object.
Answer: A) The force of gravity acting on an object.
4. If an object is moving with constant velocity, what can be said about the net force acting on it?
A) The net force is zero.
B) The net force is positive.
C) The net force is negative.
D) The net force is constant.
Answer: A) The net force is zero.
5. A car with a mass of 1000 kg accelerates at a rate of 3 m/s². What is the net force acting on the car?
A) 1000 N
B) 1500 N
C) 3000 N
D) 3500 N
Answer: C) 3000 N
6. If a force of 30 N is applied to a 10 kg object resting on a frictionless surface, what will be its acceleration?
A) 1.0 m/s²
B) 2.0 m/s²
C) 3.0 m/s²
D) 4.0 m/s²
Answer: C) 3.0 m/s²
7. Which of the following factors does not affect the acceleration of an object?
A) The mass of the object.
B) The net force acting on the object.
C) The distance traveled by the object.
D) The direction of the net force.
Answer: C) The distance traveled by the object.
8. A 2 kg block is pushed across a surface with a force of 10 N, and it accelerates at 4 m/s². What is the net force acting on the block?
A) 6 N
B) 8 N
C) 10 N
D) 14 N
Answer: B) 8 N
9. In a force versus acceleration graph, what does the slope of the line represent?
A) Mass of the object
B) Acceleration
C) Force
D) Velocity
Answer: A) Mass of the object
10. What happens to the acceleration of an object if the net force acting on it is doubled while the mass remains constant?
A) The acceleration remains the same.
B) The acceleration is halved.
C) The acceleration is doubled.
D) The acceleration is quadrupled.
Answer: C) The acceleration is doubled.

EXPERIMENT 7: MASS AND ACCELERATION
OBJECTIVES
TO DETERMINE BY GRAPHICAL ANALYSIS THE RELATIONSHIP BETWEEN THE MASS (m) AND THR ACCELERATION (a) OF AN OBJECT WITH THE FORCE ACTING ON IT BEING KEPT CONSTANT.
APPARATUS
LINEAR AIR TRACK SET UP
SET OF MASSES
MILLISECONDS TIMER
SAMPLE QUESTIONS WITH ANSWERS
1. If an object is moving at a constant acceleration, which of the following statements is true?
A) The net force acting on the object is zero.
B) The object must be in free fall.
C) The mass of the object is increasing.
D) The velocity of the object is changing.
Answer: D) The velocity of the object is changing.
2. In a vacuum, a feather and a hammer are dropped simultaneously. Which one will hit the ground first?
A) The feather
B) The hammer
C) Both hit the ground at the same time
D) It depends on the mass of each object
Answer: C) Both hit the ground at the same time
3. If two objects have the same mass but different accelerations, what can be inferred about the net forces acting on them?
A) They experience the same net force.
B) They experience different net forces.
C) The object with greater acceleration must have a smaller mass.
D) The object with smaller acceleration must have a larger mass.
Answer: B) They experience different net forces.
4. Which of the following correctly describes the relationship between mass, weight, and gravity?
A) Weight is mass multiplied by acceleration.
B) Weight is mass divided by acceleration due to gravity.
C) Weight is the mass times the gravitational acceleration (W=mgW = mgW=mg).
D) Weight is independent of mass.
Answer: C) Weight is the mass times the gravitational acceleration (W=mgW = mgW=mg).
5. A toy truck with a mass of 2 kg is accelerated at 5 m/s². What is the force exerted on the truck?
A) 5 N
B) 10 N
C) 15 N
D) 20 N
Answer: D) 10 N
6. If a 60 kg athlete pushes off the ground with a force of 480 N, what is his acceleration?
A) 6 m/s²
B) 7.2 m/s²
C) 8 m/s²
D) 9.8 m/s²
Answer: B) 8 m/s²
7. A net force of 15 N is applied to a 3 kg object. What will be the object's acceleration?
A) 3 m/s²
B) 4 m/s²
C) 5 m/s²
D) 6 m/s²
Answer: C) 5 m/s²
8. What happens to the acceleration of an object if its mass is halved while the force applied to it remains constant?
A) The acceleration doubles.
B) The acceleration is halved.
C) The acceleration remains the same.
D) The acceleration quadruples.
Answer: A) The acceleration doubles.
9. A 10 kg box is pulled with a force of 40 N. If there is a frictional force of 10 N acting against the motion, what is the net force on the box?
A) 30 N
B) 40 N
C) 50 N
D) 10 N
Answer: A) 30 N
10. If two forces of 10 N and 15 N act in the same direction on an object, what is the net force?
A) 5 N
B) 10 N
C) 15 N
D) 25 N
Answer: D) 25 N
EXPERIMENT 8: ENERGY AND ITS CONVERSION
OBJECTIVES
TO UNDERSTAND THE CONCEPT OF ENERGY AND ITS CONVERSION
APPARATUS
CURVE TRACK
BOND PAPER
MARBLE
PAPER TAPE
METER STICK
CARBON PAPER
FORMULAS
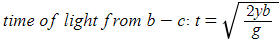
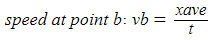
SAMPLE QUESTIONS AND ANSWERS
1. What is the principle of conservation of energy?
A) Energy can be created or destroyed.
B) Energy can be transformed from one form to another, but the total energy remains constant.
C) Energy can only exist in kinetic or potential forms.
D) Energy is always lost as heat during conversion.
Answer: B) Energy can be transformed from one form to another, but the total energy remains constant.
2. A 2 kg object is lifted to a height of 5 m. What is the gravitational potential energy gained by the object? (Use g=9.8 m/s2g = 9.8 \, \text{m/s}^2g=9.8m/s2)
A) 49 J
B) 98 J
C) 196 J
D) 245 J
Answer: B) 98 J
(Calculation: PE=mgh=2 kg×9.8 m/s2×5 m=98 JPE = mgh = 2 \, \text{kg} \times 9.8 \, \text{m/s}^2 \times 5 \, \text{m} = 98 \, \text{J}PE=mgh=2kg×9.8m/s2×5m=98J)
3. When a car accelerates, what type of energy is primarily converted?
A) Potential energy to kinetic energy.
B) Kinetic energy to thermal energy.
C) Chemical energy to kinetic energy.
D) Thermal energy to mechanical energy.
Answer: C) Chemical energy to kinetic energy.
4. A roller coaster at the top of a hill has a potential energy of 5000 J. As it descends, what happens to this potential energy?
A) It is lost as heat.
B) It is converted to kinetic energy.
C) It increases.
D) It stays the same.
Answer: B) It is converted to kinetic energy.
5. Which of the following represents an example of energy conversion in a light bulb?
A) Electrical energy to mechanical energy.
B) Electrical energy to light and thermal energy.
C) Thermal energy to electrical energy.
D) Mechanical energy to chemical energy.
Answer: B) Electrical energy to light and thermal energy.
6. A wind turbine converts which type of energy into electrical energy?
A) Kinetic energy to thermal energy.
B) Thermal energy to electrical energy.
C) Mechanical energy to electrical energy.
D) Chemical energy to electrical energy.
Answer: C) Mechanical energy to electrical energy.
7. What is the total mechanical energy of an object in motion if its kinetic energy is 150 J and potential energy is 50 J?
A) 50 J
B) 100 J
C) 150 J
D) 200 J
Answer: D) 200 J
(Calculation: Total Mechanical Energy =KE+PE=150 J+50 J=200 J= KE + PE = 150 \, \text{J} + 50 \, \text{J} = 200 \, \text{J}=KE+PE=150J+50J=200J)
8. If a pendulum swings from its highest point to its lowest point, what happens to its total mechanical energy?
A) It increases.
B) It decreases.
C) It remains constant.
D) It is converted to sound energy.
Answer: C) It remains constant.
9. A 1000 kg car is moving at a speed of 20 m/s. What is its kinetic energy?
A) 2000 J
B) 4000 J
C) 8000 J
D) 200000 J
Answer: C) 200000 J
(Calculation: KE=12mv2=12×1000 kg×(20 m/s)2=200000 JKE = \frac{1}{2} mv^2 = \frac{1}{2} \times 1000 \, \text{kg} \times (20 \, \text{m/s})^2 = 200000 \, \text{J}KE=21mv2=21×1000kg×(20m/s)2=200000J)
10. When an object falls freely, what type of energy transformation occurs?
A) Potential energy to kinetic energy.
B) Kinetic energy to potential energy.
C) Thermal energy to kinetic energy.
D) Chemical energy to potential energy.
Answer: A) Potential energy to kinetic energy.