Class 3

Your company explains that they need to cut your
salary due to business problems. They tell you they
will cut it by 10% in 2018 and again by 10% in 2019,
but in 2020 they will raise it by 20%. So in 2020, you
will be making the same amount as you are right
now (2018)
Do you agree? Explain Your reasoning? Prove it!

→ Calculation Breakdown

Assume your initial salary in 2018 is $100 for simplicity.

1. First Cut (2018):
   A 10% cut reduces your salary:

   Salary after 2018=100−(100×0.10)=100×0.90=90\text{Salary after 2018} = 100 - (100 \times 0.10) = 100 \times 0.90 = 90Salary after 2018=100−(100×0.10)=100×0.90=90

2. Second Cut (2019):
   Another 10% cut is applied to the reduced salary:

   Salary after 2019=90−(90×0.10)=90×0.90=81\text{Salary after 2019} = 90 - (90 \times 0.10) = 90 \times 0.90 = 81Salary after 2019=90−(90×0.10)=90×0.90=81

3. Raise (2020):
   A 20% increase is applied to the reduced salary:

   Salary after 2020=81+(81×0.20)=81×1.20=97.2\text{Salary after 2020} = 81 + (81 \times 0.20) = 81 \times 1.20 = 97.2Salary after 2020=81+(81×0.20)=81×1.20=97.2

Final Comparison

Your salary in 2020 is $97.20, which is 2.8% lower than your initial salary of $100.

Conclusion

You will not be making the same amount in 2020 as you were in 2018. The compounding effect of successive cuts and a raise results in a lower overall salary.

Prices of gas in:
1965: 31.2 cents
1975: 56.7 cents
1985: 119.6 cents

• How much did gas prices increase between 1975 to
  1985?

• How much cheaper was gas in 1965 compared to
  1975?

1. Gas Price Increase Between 1975 and 1985

To calculate the absolute and relative increase:

Absolute Increase:

Absolute Increase=Price in 1985−Price in 1975\text{Absolute Increase} = \text{Price in 1985} - \text{Price in 1975} Absolute Increase=Price in 1985−Price in 1975Absolute Increase=119.6−56.7=62.9 cents\text{Absolute Increase} = 119.6 - 56.7 = 62.9 \, \text{cents} Absolute Increase=119.6−56.7=62.9cents

Relative Increase:

Relative Increase=(Absolute IncreasePrice in 1975)×100\text{Relative Increase} = \left( \frac{\text{Absolute Increase}}{\text{Price in 1975}} \right) \times 100 Relative Increase=(Price in 1975Absolute Increase​)×100Relative Increase=(62.956.7)×100≈110.9%\text{Relative Increase} = \left( \frac{62.9}{56.7} \right) \times 100 \approx 110.9\% Relative Increase=(56.762.9​)×100≈110.9%

Answer: Gas prices increased by 62.9 cents (about 111%).

2. How Much Cheaper Gas Was in 1965 Compared to 1975

To calculate the absolute and relative difference:

Absolute Difference:

Absolute Difference=Price in 1975−Price in 1965\text{Absolute Difference} = \text{Price in 1975} - \text{Price in 1965} Absolute Difference=Price in 1975−Price in 1965Absolute Difference=56.7−31.2=25.5 cents\text{Absolute Difference} = 56.7 - 31.2 = 25.5 \, \text{cents} Absolute Difference=56.7−31.2=25.5cents

Relative Difference:

Relative Difference=(Absolute DifferencePrice in 1975)×100\text{Relative Difference} = \left( \frac{\text{Absolute Difference}}{\text{Price in 1975}} \right) \times 100 Relative Difference=(Price in 1975Absolute Difference​)×100Relative Difference=(25.556.7)×100≈44.9%\text{Relative Difference} = \left( \frac{25.5}{56.7} \right) \times 100 \approx 44.9\% Relative Difference=(56.725.5​)×100≈44.9%

Answer: Gas was 25.5 cents cheaper in 1965 compared to 1975, which is about 45% cheaper.

1. Inflation Rate Between 2007 and 2008

The formula to calculate the inflation rate is:

Inflation Rate=CPI in 2008−CPI in 2007CPI in 2007×100\text{Inflation Rate} = \frac{\text{CPI in 2008} - \text{CPI in 2007}}{\text{CPI in 2007}} \times 100Inflation Rate=CPI in 2007CPI in 2008−CPI in 2007​×100

From the table:

• CPI in 2007 = 207.3

• CPI in 2008 = 215.3

Inflation Rate=215.3−207.3207.3×100=8.0207.3×100≈3.86%\text{Inflation Rate} = \frac{215.3 - 207.3}{207.3} \times 100 = \frac{8.0}{207.3} \times 100 \approx 3.86\%Inflation Rate=207.3215.3−207.3​×100=207.38.0​×100≈3.86%

Answer: The inflation rate between 2007 and 2008 is approximately 3.86%.

2. Salary Adjustment to Keep Pace with Inflation

If a salary of $50,000 is to keep pace with inflation, it needs to increase by the same percentage as the inflation rate.

Increase in Salary=Current Salary×Inflation Rate\text{Increase in Salary} = \text{Current Salary} \times \text{Inflation Rate}Increase in Salary=Current Salary×Inflation RateIncrease in Salary=50,000×0.0386=1,930\text{Increase in Salary} = 50,000 \times 0.0386 = 1,930Increase in Salary=50,000×0.0386=1,930New Salary=Current Salary+Increase in Salary=50,000+1,930=51,930\text{New Salary} = \text{Current Salary} + \text{Increase in Salary} = 50,000 + 1,930 = 51,930New Salary=Current Salary+Increase in Salary=50,000+1,930=51,930

Answer: The salary would need to increase by $1,930 in absolute terms to keep pace with inflation.

]

Lie Detector / Polygraph

Should polygraph tests be used as an acceptable form of evidence in a criminal trial?

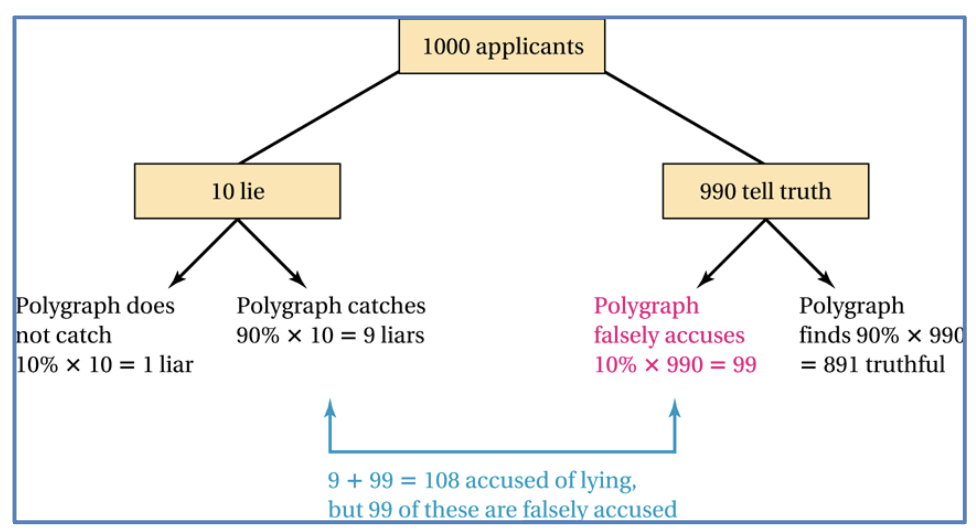
Suppose that 1000 job applicants take a
polygraph test, 1 in 100 lie, and the
polygraph is 90% accurate. How many of
those applicants who were accused of
lying were actually telling the truth?
Positive = Lie
Negative = Truth

→ Total number of applicants = 1000

• Proportion who lie = 1 in 100, so P(Lie)=1100=0.01P(\text{Lie}) = \frac{1}{100} = 0.01P(Lie)=1001​=0.01

• Proportion who tell the truth = 99 in 100, so P(Truth)=99100=0.99P(\text{Truth}) = \frac{99}{100} = 0.99P(Truth)=10099​=0.99

• Polygraph accuracy = 90%, meaning:

  • If someone lies, the test will correctly identify them as lying 90% of the time: P(Positive test∣Lie)=0.9P(\text{Positive test} | \text{Lie}) = 0.9P(Positive test∣Lie)=0.9

  • If someone tells the truth, the test will correctly identify them as truthful 90% of the time, meaning the false positive rate is 10%: P(Positive test∣Truth)=0.1P(\text{Positive test} | \text{Truth}) = 0.1P(Positive test∣Truth)=0.1

We need to calculate the number of applicants who were accused of lying (i.e., those with a positive test result) but were actually telling the truth.

Bayes' Theorem Formula:

Bayes' Theorem helps us calculate the probability of being truthful given a positive test result:

P(Truth∣Positive test)=P(Positive test∣Truth)×P(Truth)P(Positive test)P(\text{Truth} | \text{Positive test}) = \frac{P(\text{Positive test} | \text{Truth}) \times P(\text{Truth})}{P(\text{Positive test})}P(Truth∣Positive test)=P(Positive test)P(Positive test∣Truth)×P(Truth)​

Where:

• P(Positive test)P(\text{Positive test})P(Positive test) is the total probability of getting a positive test, which can be calculated using the law of total probability:

P(Positive test)=P(Positive test∣Lie)×P(Lie)+P(Positive test∣Truth)×P(Truth)P(\text{Positive test}) = P(\text{Positive test} | \text{Lie}) \times P(\text{Lie}) + P(\text{Positive test} | \text{Truth}) \times P(\text{Truth})P(Positive test)=P(Positive test∣Lie)×P(Lie)+P(Positive test∣Truth)×P(Truth)

Now, let's calculate step by step.

Out of the applicants who were accused of lying (those with a positive test result), approximately 99 were actually telling the truth.

Test Results
true positive → A test correctly reports a positive
result

false positive → A test incorrectly reports a
positive result

true negative → A test correctly reports a
negative result

false negative → A test incorrectly reports a
negative result

Lie Detector /Polygraph