Bias-Variance Trade-Off (Pt.1)

1/4/2024

The U shape from test MSE comes from the result of two competing properties.

E\left( y_0 - \hat{f}(x_0) \right)^2 = \text{Var}\left( \hat{f}(x_0) \right) + \left[ \text{Bias}\left( \hat{f}(x_0) \right) \right]^2 + \text{Var}(\epsilon).

The variance of the model versus the bias of the model. This equations tells us that to lower the overall expected test MSE we have to minimize the variance and the bias of the model.

How do we computer the overall test MSE?

The overall average test MSE can be computed by average E\left( y_0 - \hat{f}(x_0) \right)^2 for each x_0 of multiple training sets

How do we select a model that has minimal MSE?

We need to select a learning model that simultaneously has low variance and low bias

What is Variance?

The amount we expect the model \hat{f} to change if we use a different training set

What are some qualities of Variance?

• Inherently non-negative

What are some qualities of Bias?

• Inherently non-negative

What is a characteristic of a model with high variance?

Small changes in a dataset can make drastic changes in \hat{f}

What is the relationship between flexibility of a model and its variance?

The more flexible the model the higher the variance tends to be

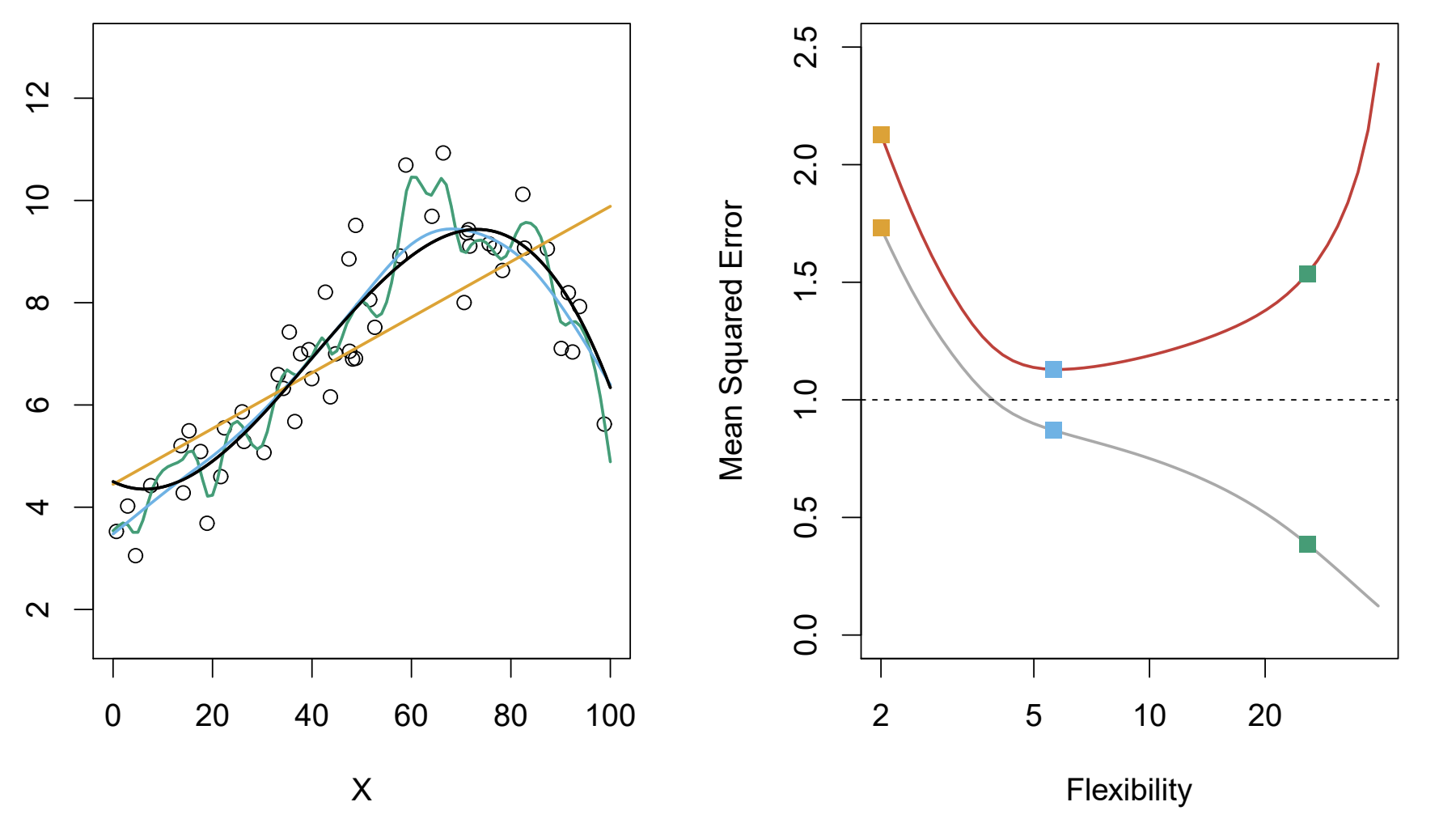
Given the above graph, which model has the lowest variance?

The orange model since it is relatively inflexible compared to the green and blue lines.