cogsci200 lecture notes

03.05.24 (Computation I)

• fundamentals: primitive objects and relations

• all thinking processes = computation

• Computational Theory of Mind: all mentation is computation, foundational claim about mind/brain computation in cog sci

  • “The mind is what the brain does: The brain processes information, and thinking is a kind of computation.” — Pinker

• central assumption for cognitive science = brain is an information-processing system: cognition is computation

• mind-body problem: mind is entirely distinct from body (thinking thing vs. extended thing)

• computer is NOT a good metaphor for the mind

  • rather, mind and computer both compute and embody intelligence for the same reason

  • theory of aerodynamics and computation are both abstract and general

    • aerodynamics is applied to birds, planes, etc.

Computation

• execution of algorithms that implement functions

• physical processes transforming physical patterns of symbols

• Alan Turing

• What makes thought and intelligence possible? - Computation

Execution of Algorithms

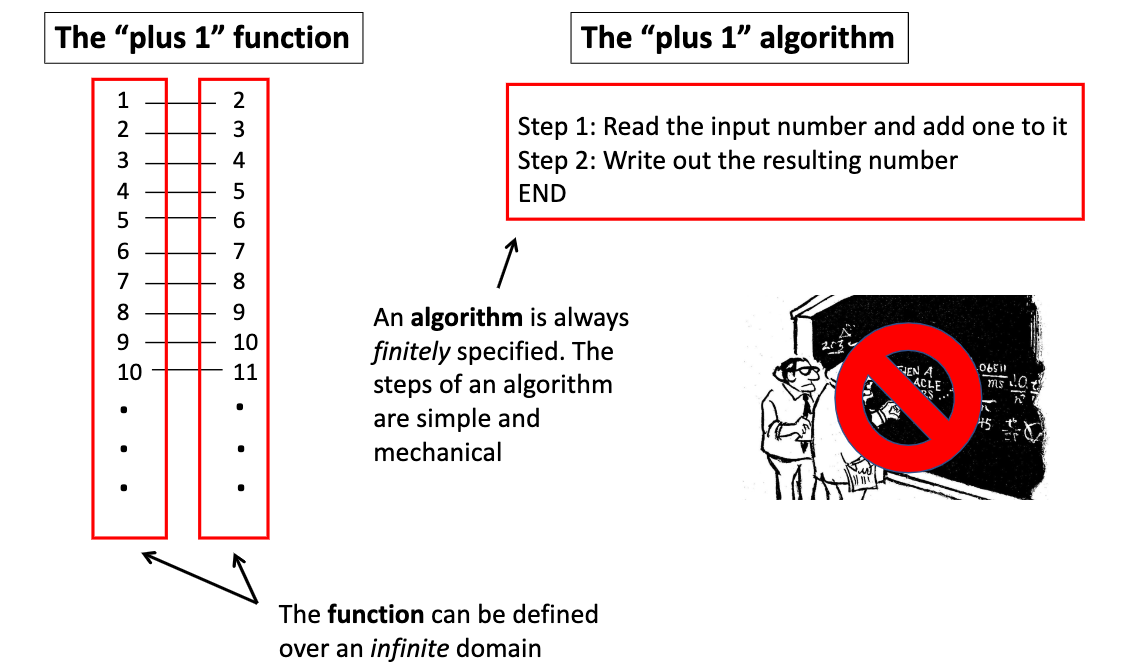
• algorithm = execution of a computational procedure

• properties of algorithm

  • maps one set of symbols (input) into another set of symbols (output)

  • finitely specifiable (directions, duration, complete)

  • execution does not itself require “intelligence”

Symbols

• physical states of bits of matter, chips in a computer or neurons in the brain (Johnson-Laird reading)

• symbolize things in the world because they are triggered by those things via sense organs

• symbols = patterns that denote or encode information

Functions

• algorithms = step-by-step recipes that produce function

• function maps each member of one set of symbols to a single member of another set of symbols

  • each input has unique output

• palindrome is a function, reads same front to back and back to front

  • ex. mr owl ate my metal worm

• plus 1 algorithm

  • steps are simple and mechanical

  • function can be defined over an infinite domain

Quiz 10

• Q1: B — Foundational claim in cognitive science → Thinking is a kind of computation

• Q2: B — execution of algorithms itself requires intelligence (false)

• Q3: D — According to the reading by Steven Pinker, the computational theory of mind (A & B: resolves mind-body problem, mental state = information manifested as symbols which are physical brain states)

Alan Turing

• key part of WWll secret effort that led to breaking of Germany’s enigma machine coding scheme

• primitive building blocks of computation

  • Turing Machine = idea/concept, not physical machine

    • contains minimal components that a physical machine needs for computation

    • Turing provided minimal formalization of computation

• what can be constructed from primitives

  • Turing machines are maximally powerful → can compute any computable function

  • certain Turing machines are maximally flexible → can execute any algorithm

• Turing Machine = computer

  • from 1600s-1940s, “computer” refers to people

    • women during the war when husbands were out on field

• ex. woman thinking and reasoning to solve problems

  • goal: find minimal set of things needed for her to engage in computation

  • some components are necessary for her to compute: reading ability, her memory, etc.

    • other things are not: hair texture, clothing

  • stipulate that paper is endless

  • variety of symbols, binary code

  • state memory

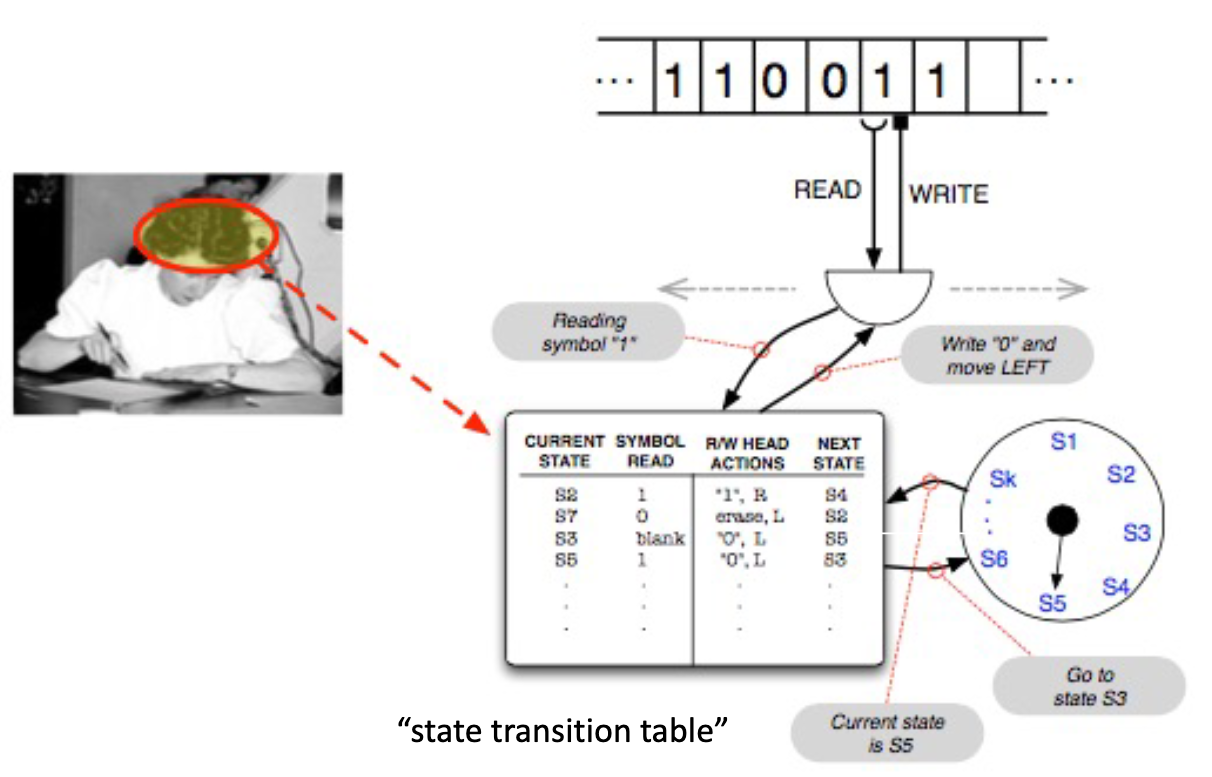
  • state transition table contains step-by-step recipe for calculating function

    • input and how to map it to output

Turing machines and five primitives of computation

1. unlimited tape divided into cells that are either blank or have single symbol

2. list of symbols that is finite

3. read/write head positioned at a single cell on the tape and can read the symbol at that cell and write or erase a symbol

4. state memory = memory of internal states (finite)

5. finite transition table that determines the control of the Turing Machine with the following instructions:

• if you are in one state and read a particular symbol, then write particular symbol on the tape, move R or L, and change state

• needs input the machine reads, state the machine is in (find relevant rule), 2 input parts and 3 output parts

  • order the rules are listed in do not matter, depends on the input and state

03.07.24 (Computation ll)

Quiz 11

• Q1: D — Turing machines (neither A or B)

• Q2: A — Which component of a Turing Machine is infinite? Tape

• Q3: B — Church-Turing thesis states that all conceivable functions can be computed by some Turing machine (false)

  • conceivable is not the same as computable

Marr’s levels of explanation and computation

• functional: mapping of input to output

• algorithmic: finitely specified computational procedure that generates specified mapping relation

• physical: substrates in which algorithm is realized or implemented

• same function can be computed by multiple distinct algorithms

  • single algorithm can be realized in multiple different physical substrates

Multiple realizability

• single algorithm can be realized in multiple distinct physical substrates

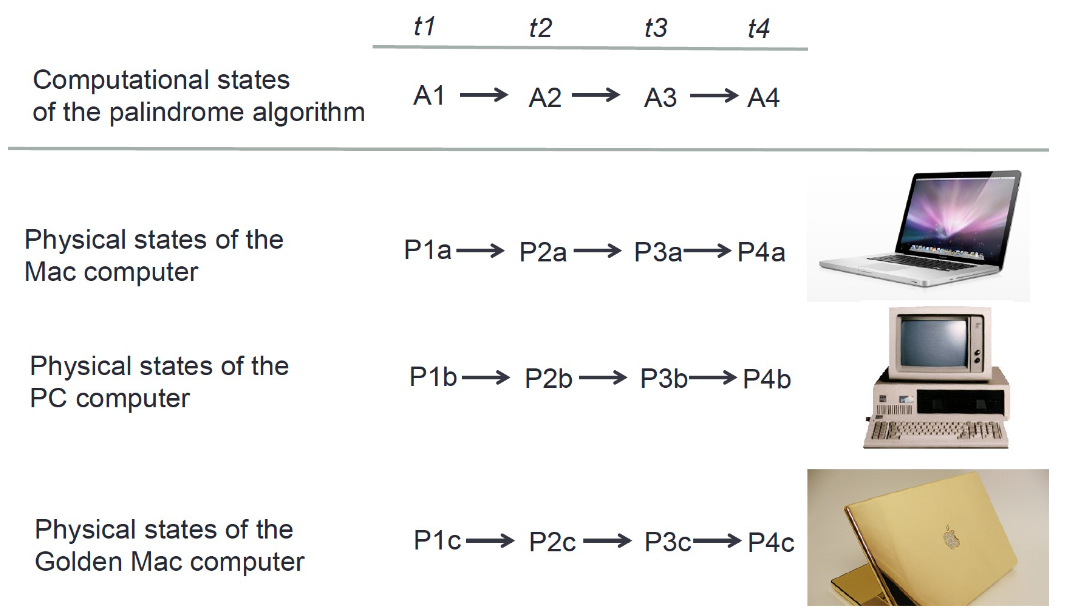
• if all mentation is computation, then mental states and processes are also multiply realizable → a single mental state or process can be implemented in multiple different physical substrates

  • input-output equivalence

Turing claims

1. TM are maximally powerful — every element of the class of computable functions can be computed (Church-Turing Thesis)

2. There are Universal Computing Machines that are maximally flexible

Church-Turing thesis

• A function is “computable” if and only if it can be computed by some Turing Machine

  • class of computable functions and the class of functions that can be computed by a Turing Machine are one and the same

    • function is “computable” if and only if there is some well-specified finite procedure for computing the function

• thesis, not theorem; evidence makes it very plausible

Evidence for Church-Turing thesis

• every formalism proposed as the basis of computation since 1936 has been shown to be mathematically equivalent to TM in computational power

• large classes of functions have been proven computable by TM

• increasingly complex computational functions continue to be implemented on physical computing machines

Is increasing TM power possible (increase set of possible computable functions)/disprove Church-Turing thesis

• NO

  • allow it to jump to any cell on the tape

  • increase set of symbols

  • give it additional read/write heads

  • allow it to operate non-deterministically or probabilistically

Implications of C-T thesis

• speculative argument

  • our mental capacities can be readily understood as functions

  • they are computable functions since our mind in fact does compute them

  • plausible claim: therefore, functions computed by these mental capacities can be computed by TM

  • conclusion: therefore, the five computational primitives are sufficient to explain the operation of these capacities

Limits on what we can construct

• think of C-T thesis and Turing’s minimal formalization of computation as a big breakthrough (characterization of what can be computed in physical universe)

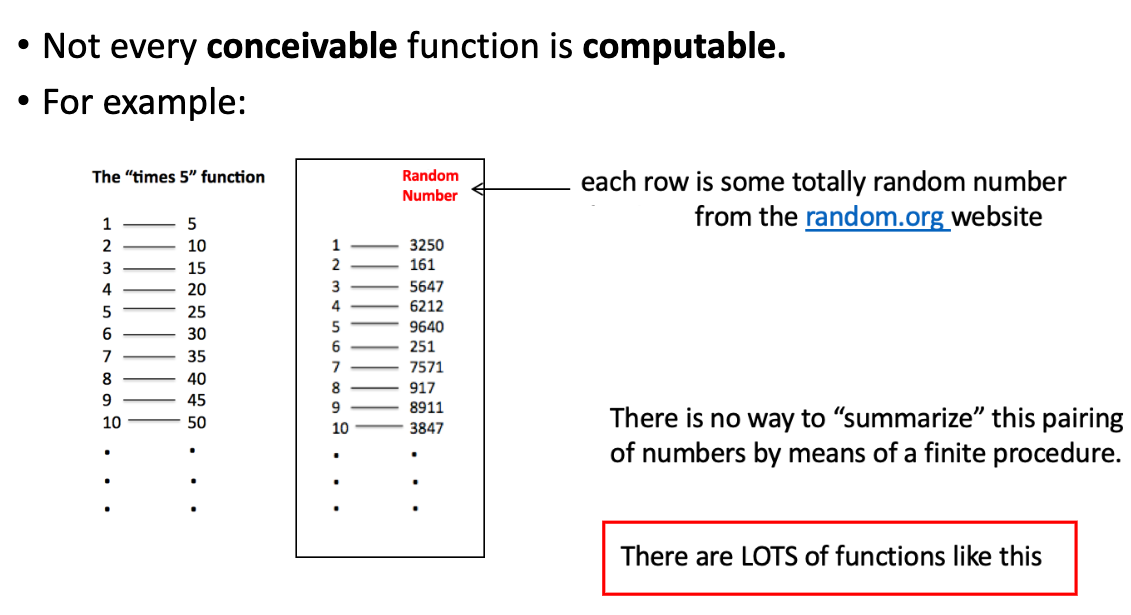
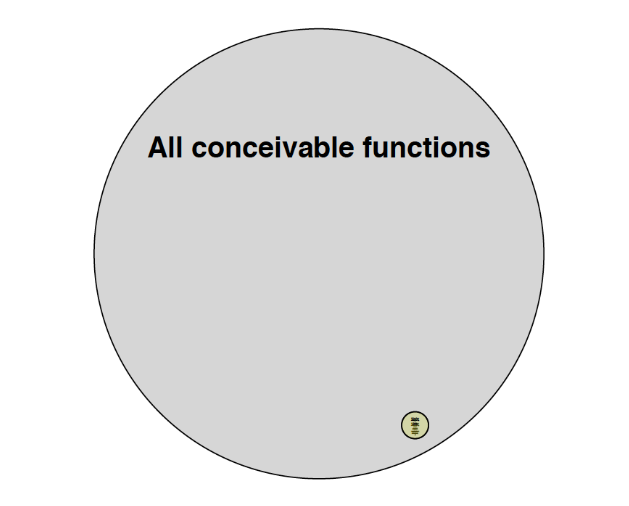
• NOT every conceivable function can be computed/is computable

Halting Problem

• example of how conceivable does not equal computable

• TM that will take input of description of another TM and some input for that machine, then halt with a 1 on the tape if the other TM will halt, and 0 otherwise → such a TM does not exist

• speed and processing power not to be conflated with computing power

• proof by contradiction; algorithm decides whether it stops or not (no algorithm can determine whether another computer program will halt or run indefinitely)

Class of computable functions: Class of all conceivable functions: (previous class takes up very tiny part)

Interesting Problem

• do not want to add new TM for every function that brains can compute

• How do we explain how a single brain can do all the things that brains can do?

• plausible that we have some modules for specific functions, but also plausible that the mind/brain is capable of more general, all-purpose computation

• middle ground position: only some elements of the mind (especially perception) are modular

• possible answer: universal computing machines

Universal Computing Machines

• single TM that can compute every computable function

• can simulate any other machine (taking as input a description of the function to compute and its input)

• maximally flexible

does not change the relationship of all conceivable functions (same as previous venn diagram)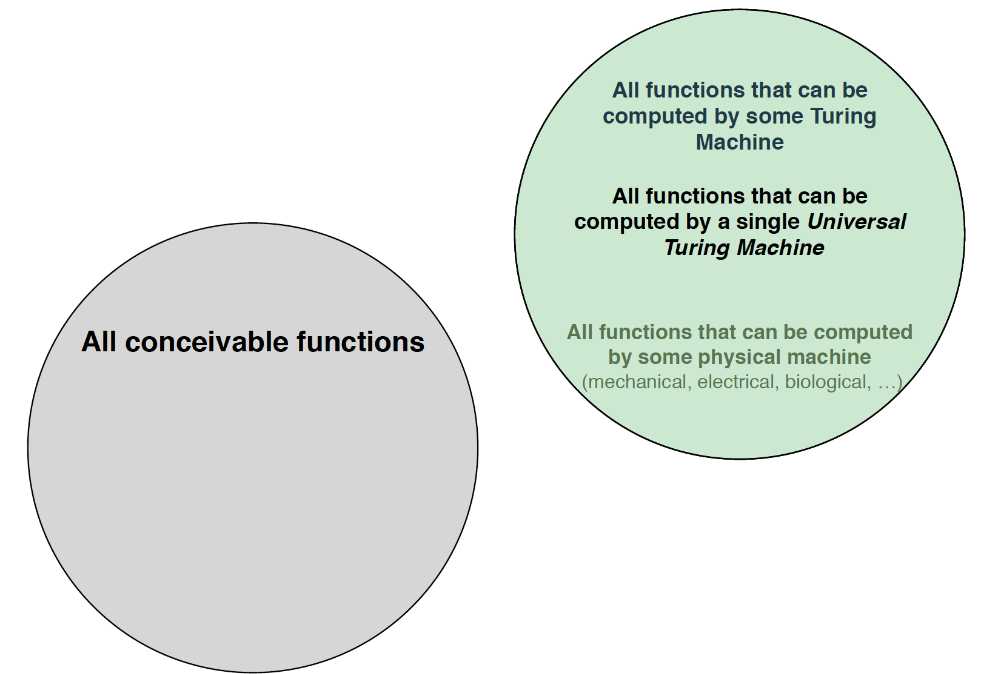03.08.24 Discussion

• domain for