Chapter 17 - Simple Harmonic Motion

Simple Harmonic Motion

• Simple harmonic motion describes any periodic motion that is the result of a restoring force that is proportional to the displacement

  • The motion of a vibrating mass-spring system or a pendulum is an example of a simple harmonic motion

• Because simple harmonic motion involves a restoring force, every simple harmonic motion is a back-and-forth motion over the same path

  

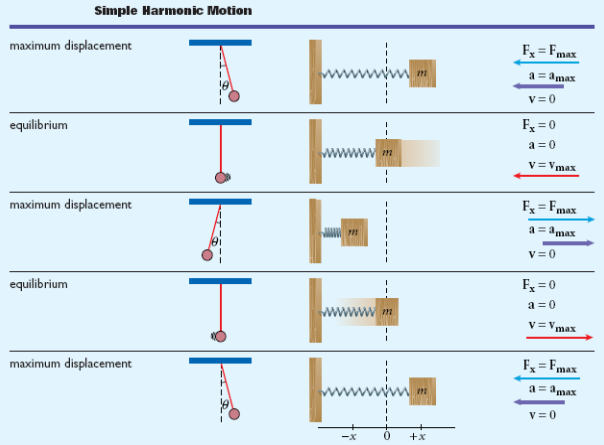
• A simple pendulim consists of a mass called a bob, which is attached to a fixed string

  • Like the spring, the pendulum oscillates, or moves back and forth at regular motion

  

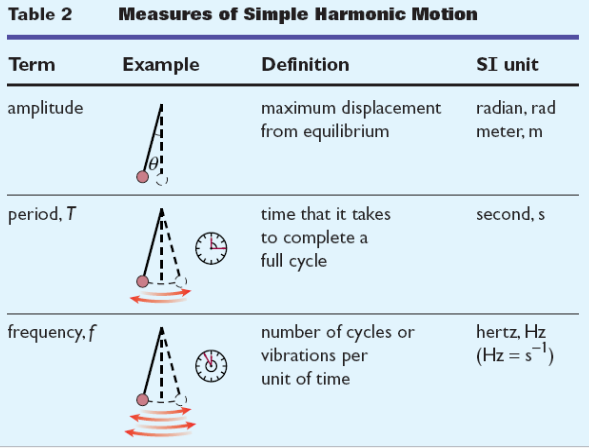
• Amplitude of motion is the maximum displacement from equilibrium

  • For a pendulum,

    • measured by how high the bob is lifted above its equilibrium point (also angle it is let go from)

  • For a mass-spring system,

    • the maximum amount the spring is stretched or compressed from its equilibrium position

• units —> radian, degrees and meters

• The period (T) is the time that it takes a complete cycle to occur

  • The SI unit of period is seconds (s)

• The frequency (f) is the number of cycles or vibrations per unit of time

  • The SI unit of frequency is hertz (Hz)

  • Hz=s^-1

  f = 1/T or T = 1/f

  

• The period of a simple pendulum depends on the length L and on the acceleration due to gravity g

  T=2\pi\sqrt{\frac{L}{g}} or period=2\pi\sqrt{\frac{leng\operatorname{th}}{\left.free-fall\right)acceleration}}

• The period does not depend on the mass of the bob or on the amplitude (for smaller angles)

EXAMPLE:

1. A 1.3 m long pendulum swings back in forth in a classroom. What is its period?

   T=2\pi\sqrt{\frac{L}{g}}

   T=2\pi\sqrt{\frac{1.3}{9.8}}

   T=2\pi\sqrt{0.133}

   T=2\pi\left(0.364\right)

   T=2.29 seconds

Waves

• A rhythmic disturbance that carries energy through matter or space

  • Mechanical waves: require a medium to transport energy

    • Example: water waves, sound waves, springs

  • Electromagnetic waves: do not require a medium, can travel through vacuum

    • Example: X-rays, light, radio waves

• Oscillation is the back and forth motion that is repeated

• Simple harmonic motion has no friction involved, the motion continues the same way, never changing

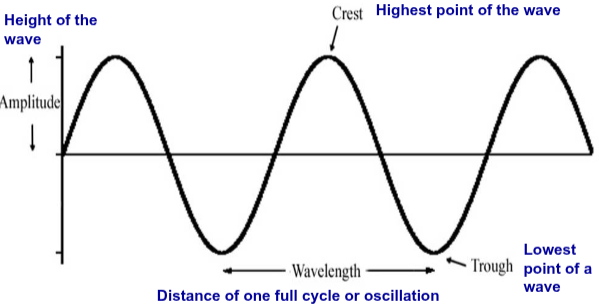
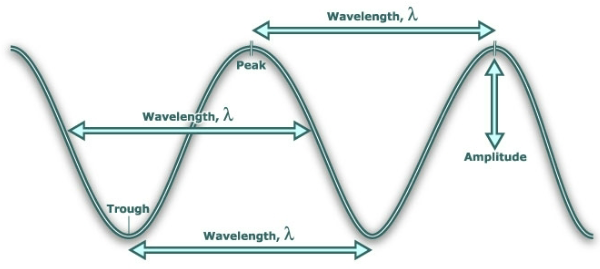
• Waves can have multiple crests and troughs

• Amplitude is measured in meters

• The wavelength can be measured anywhere on the wave

  • Easiest way to measure is usually crest to crest

  • Any distance between successive (non-repeating) parts of a wave

  

• Waves transfer energy by the vibration of matter

• Waves are often able to transport energy effciently

• The rate at which a wave transfers energy depends on the amplitude

• The greater the amplitude, the more energy a wave carries in a given time interval

• Waves are disturbances in a medium

• When water drops hit water, it creates a disturbance in the water

  • The disturbance moves, not the water

• Period —> T

  • Time it takes for one complete wavelength

    • T = time it takes/# of oscillations

    • Measured in seconds (s)

• Frequency —> F

  • How frequently the oscillation occurs

  • How many oscillations occur in 1 second

    • F = number of oscillations/time

    • Measured in Hertz (Hz) = 1/second

• Frequency and Periof are very closely related

  • They are each other’s inverse

T=\frac{1}{f} and f=\frac{1}{T}

• Types of mechanical waves

  • Transverse: particles travel perpendicular to the motion of the wave

    • ←· → ←·→ ←·→ ←·→ ←·→ ←·→

  • Longitudinal: particles travel parallel to the motion of the wave

  • Water waves close to the shore are actually called surface waves because they are both transverse and longitudinal

• We can measure the velocity of the wave the way we always measured it

  velocity = displacement/time or v=\frac{d}{t}

  OR

  v=\frac{\lambda}{T} aka V = wavelength/period

• but more commonly seen as v=\lambda f since f=\frac{1}{T}

  • λ is lambda and stands for wavelength

EXAMPLE:

1. A surfer notices that in 10 seconds, 4 ocean waves strike the beach. He also estimates that the waves are 3 m apart. What is the speed of the waves?

   In 10 seconds, 4 waves pass, so \frac{10}{4}=2.25 sec per 1 wave

   V=\frac{D}{t}

   V=\frac{3m}{2.5\sec}

   V = 1.2 m/s

2. A radio wave is oscillating at a rate of 43 times per second. The distance between a crest and a trough is 0.2 m. What is the wave speed?

   V=\lambda f

   V=43\left(0.4\right)

   V= 17.2 m/s

Superposition

• Superposition is also called interference

  • 2 or more waves are always needed

• Waves collide with each other to make a new wave, even if for only a brief amount of time

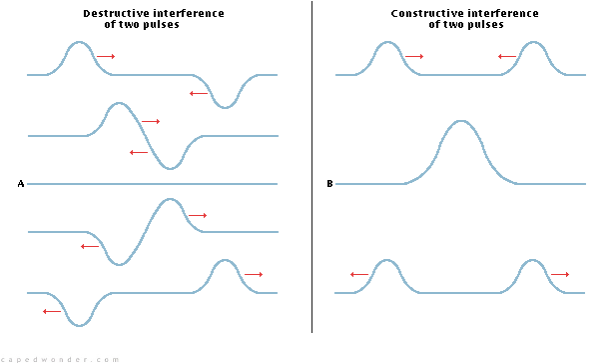
• There are 2 types of interference:

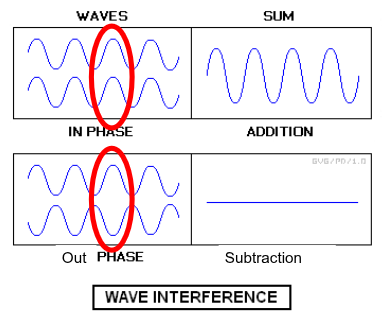
  • Constructive: waves are in-phase and add together

  • Destructive: waves are out of phase and subtract

  

Standing Waves

• They appear to be ‘standing’ still in their left to right motion

  • They are in constant motion though!

• Standing waves can occur when a wave interferes with it’s reflected self

• There are two main parts of the standing wave:

  • The node

    • points of complete destructive interference

    • do not move

  • The antinode

    • points of complete constructive interference

    • largest amplitude points of the standing wave

  

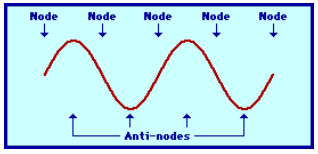
• On a musical instrument, the strings are fixed at both ends

• This means that there must be nodes at each end, and this limits the possible vibrations *or oscillations) of the string

• Each one of these standing waves (below) have the wavelengths that produce a frequency known as harmonics

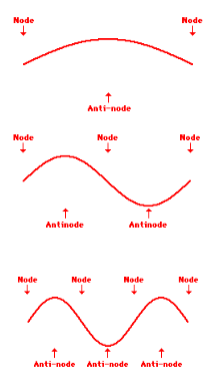
• The first standing wave has what is known as the fundamental frequency, f

• The second standing wave as the second harmonic, 2f

• The third standing wave has the third harmonic 3f