Chapter 8: Gases
8.1: Properties of Gases
- Kinetic Molecular Theory of Gases: A model for the behavior of a gas that helps us understand gas behavior.
Kinetic Molecular Theory of Gases
- A gas consists of small particles 1atoms or molecules2 that move randomly with high velocities.
- The attractive forces between the particles of a gas are usually very small.
- The actual volume occupied by gas molecules is extremely small compared with the volume that the gas occupies.
- Gas particles are in constant motion, moving rapidly in straight paths.
- The average kinetic energy of gas molecules is proportional to the Kelvin temperature.
Properties That Describe a Gas
| Property | Description | Units of Measurement |
|---|---|---|
| Pressure (P) | The force exerted by a gas against the walls of the container. | atmosphere (atm); millimeters of mercury (mmHg); torr; pascal (Pa) |
| Volume (V) | The space occupied by a gas. | Liter (L); milliliter (mL) |
| Temperature (T) | The determining factor of the kinetic energy and rate of motion of gas particles. | degree Celsius (°C); Kelvin (K) |
| Amount (n) | The quantity of gas present in a container. | Grams (g); moles (n) |
Units for Measuring Pressure
| Units | Abbreviation | Unit Equivalent to 1 atm |
|---|---|---|
| Atmosphere | atm | 1 atm |
| Millimeters of Hg | mmHg | 760 mmHg |
| Torr | torr | 760 torr |
| Inches of Hg | in. HG | 29.9 in. Hg |
| Pounds per square inch | lb/in^2 (psi) | 14.7 lb/in.^2 |
| Pascal | Pa | 101 325 Pa |
| Kilopascal | kPa | 101.325 kPa |
8.2: Pressure and Volume
Boyle’s Law: The pressure increases if volume decreases; pressure decreases if volume increases.
The inverse relationship between the pressure and volume of a gas.
The law states that the volume of a sample gas changes inversely with the pressure of the gas as long as there is no change in the temperature or amount of gas.
If the volume or pressure of a gas sample changes without any change in the temperature or in the amount of the gas, then the final volume will give the same PV product as the initial pressure and volume.
Formula:
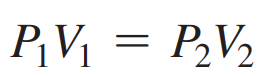
Sample Problem
Oxygen gas is delivered through a face mask during oxygen therapy. The gauge on a 12-L tank of compressed oxygen reads 3800 mmHg. How many liters would this same gas occupy at a pressure of 0.75 atm when temperature and amount of gas do not change?
Step 1: Organize the data in a table of initial and final conditions.

Step 2: Rearrange the gas law equation to solve for the unknown quantity.

Step 3: Substitute values into the gas law equation and calculate

8.3: Temperature and Volume
Charles’s Law: As temperature of a gas increases, its volume increases; if its temperature decreases, volume decreases.
It states that the volume of a gas is directly related to the temperature when there is no change in the pressure of amount of gas.
A direct relationship is one in which the related properties increase or decrease together.
Formula:
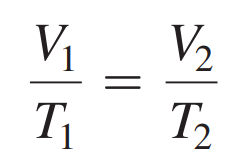
Sample Problem
A sample of Oxygen gas at 427 ° C has a volume of 100 liters. When cooled its volume is reduced to 73 liters. What is the temperature when the volume is 73 liters?
Step 1: Organize the data in a table of initial and final conditions.

Step 2: Rearrange the gas law equation to solve for the unknown quantity.

Step 3: Substitute values into the gas law equation and calculate
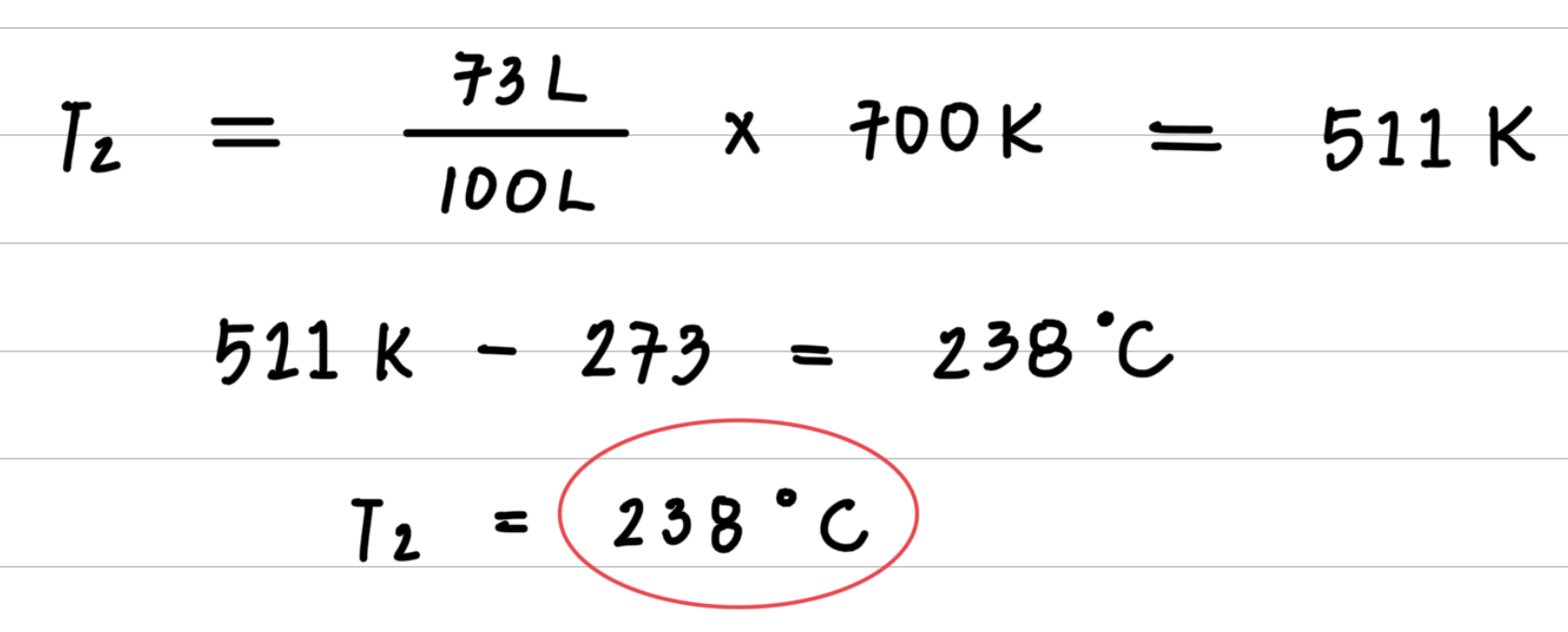
8.4: Temperature and Pressure
Gay-Lussac’s Law: As temperature of a gas increases, its pressure increases; if its temperature decreases, pressure decreases.
The pressure of a gas is directly related to its Kelvin temperature.
An increase in temperature increases the pressure of a gas and a decrease in temperature decreases the pressure of the gas, as long as the volume and amount of gas do not change.
Formula:
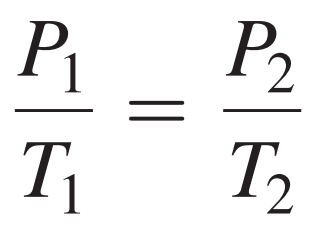
Sample Problem
Aerosol containers can be dangerous if they are heated, because they can explode. Suppose a container of hair spray with a pressure of 4.0 atm at a room temperature of 25 °C is thrown into a fire. If the temperature of the gas inside the aerosol can reach 402 °C, what will be its pressure in atmospheres? The aerosol container may explode if the pressure inside exceeds 8.0 atm. Would you expect it to explode?
Step 1: Organize the data in a table of initial and final conditions.

Step 2: Rearrange the gas law equation to solve for the unknown quantity.

Step 3: Substitute values into the gas law equation and calculate

8.5: The Combined Gas Law
All of the pressure–volume–temperature relationships for gases combined into a single relationship.
The combined gas law is used to determine the effect of changes in two of the variables on the third.
Formula:

Sample Problem
A 25.0-mL bubble is released from a diver’s air tank at a pressure of 4.00 atm and a temperature of 11 °C. What is the volume, in milliliters, of the bubble when it reaches the ocean surface, where the pressure is 1.00 atm and the temperature is 18 °C? 1Assume the amount of gas in the bubble does not change.2
Step 1: Organize the data in a table of initial and final conditions.

Step 2: Rearrange the gas law equation to solve for the unknown quantity.

Step 3: Substitute values into the gas law equation and calculate

8.6: Volume and Moles
Avogadro’s Law: If the moles of gas are increased, the volume must increase; if the moles of gas are decreased, the volume must decrease.
It states that the volume of a gas is directly related to the number of moles of a gas when temperature and pressure do not change.
Standard temperature is exactly 0 °C (273 K).
Standard pressure is exactly 1 atm (760 mmHg).
Formula:

Sample Problem
L sample of gas is determined to contain 0.5 moles of nitrogen. At the same temperature and pressure, how many moles of gas would there be in a 20 L sample?
Step 1: Organize the data in a table of initial and final conditions.
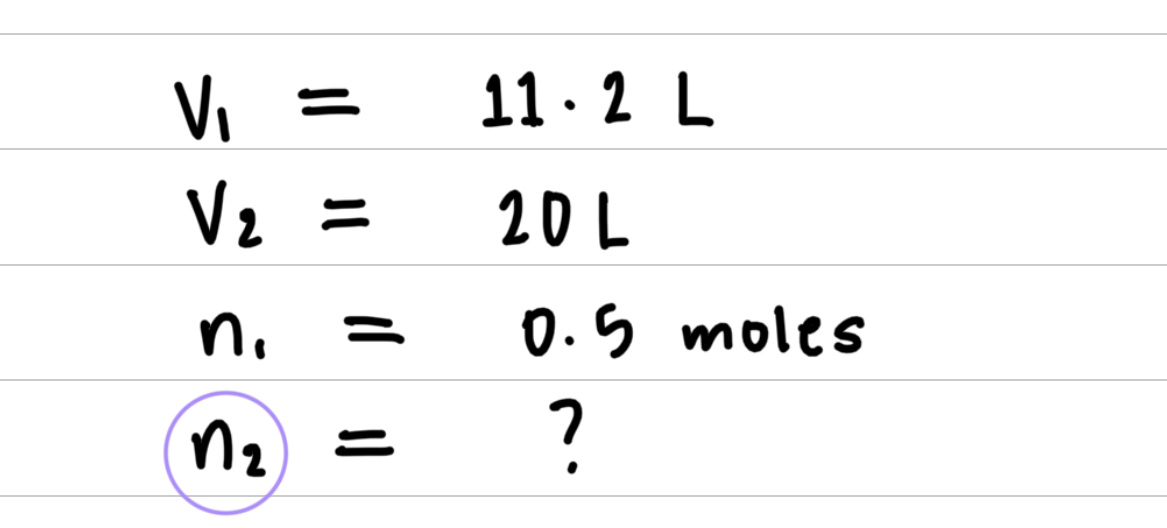
Step 2: Rearrange the gas law equation to solve for the unknown quantity.

Step 3: Substitute values into the gas law equation and calculate

8.7: Partial Pressures
Partial Pressure: It is the pressure it would exert if it were the only gas in the container.
Dalton’s Law: States that the total pressure of a gas mixture is the sum of the partial pressures of the gases in the mixture.
Formula:
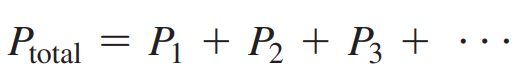
Sample Problem
A heliox breathing mixture of oxygen and helium is prepared for a scuba diver who is going to descend 200 ft below the ocean surface. At that depth, the diver breathes a gas mixture that has a total pressure of 7.00 atm. If the partial pressure of the oxygen in the tank at that depth is 1140 mmHg, what is the partial pressure, in atmospheres, of the helium in the breathing mixture?
Step 1: Write the equation for the sum of the partial pressures.

Step 2: Rearrange the gas law equation to solve for the unknown pressure.

Step 3: Substitute known pressures into the equation and calculate the unknown partial pressure.
