W7 Levels of measurement & descriptive statistics

Page 4: Learning Outcomes

By the end of the lecture, students should be able to:

• Explain nominal, ordinal, interval, and ratio data with examples.

• Demonstrate understanding of measures of central tendency (mean, median, mode) and spread (variance, standard deviation).

• Identify basic mathematical equations related to statistics.

Page 6: Types of Statistics

• Descriptive Statistics:

  • Summarize and describe datasets

  • central tendency and spread.

  • Concerned with concrete/known values.

• Inferential Statistics:

  • Use probability to infer conclusions about larger population samples.

  • Abstract/estimated values.

Page 8: Levels of Measurement

• Key question: How much detail do the data convey?

• Four levels:

  1. Nominal

  2. Ordinal

  3. Interval

  4. Ratio

Page 9: Nominal Data

• Also called categorical data; lowest information level.

• Categories have no numerical relationships (figures) between categories

• Examples include gender (male/female/non-binary), language proficiency (bilingual/monolingual), and colour categories.

• only tells us the datapoint is in one category: groups are separated

Page 10: Ordinal Data

• Ranked positions; numbers do not represent counts

• the exact interval between positions is still unknown (winner, second, third)

• Examples: ranks in competitions, Likert scales (e.g., agree/disagree).

Page 11: Interval Data

• Equal units; distances between scale points are consistent.

• Examples include IQ scores, temperature (Celsius/Fahrenheit).

• Can calculate a range of stats - mean, median etc.

Page 13: Ratio Data

• Interval data with a true zero, allowing for ratios.

• Cannot take negative values.

• Examples include height, weight, and duration of time.

Page 12: Likert Scale Debate

• Likert scale can be ordinal or interval based on design.

  • Single-item scores treated as ordinal

  • combined multiple items may be treated as interval.

Page 14: Measurement Levels Summary

• Nominal: Categorical data; frequency count only.

• Ordinal: Orders data; mode and median applicable.

• Interval/Ratio: Mean and standard deviation can be calculated.

Page 19: Descriptive Statistics

• central tendency

  • most typical score

• dispersion (value variance)

  • How much do the values vary around the central value

• Both measures are necessary for a complete data understanding.

Page 20: Measures of Central Tendency

1. Mean:

   • Arithmetic average; sum of scores/number of scores.

2. Median:

   • Midpoint dividing scores, half the scores above the median and half above, half below.

3. Mode:

   • Most frequent score; the simplest measure of central tendency.

Page 21: Central Tendency Considerations

• Mean is most commonly, however its the most sensitive to outliers.

• If data contains extreme values, median is preferred because it provides a better indication of the typical score

• Visualize data to understand its structure.

• Reference the "datasaurus" for illustration of data visualization importance.

Page 27: Data Distribution Overview

• If a dataset is symmetrical, then the mean, mode and median are all the same.

Page 29: Measures of Spread/Dispersion

1. Range:

   • Difference between highest and lowest score; sensitive to outliers.

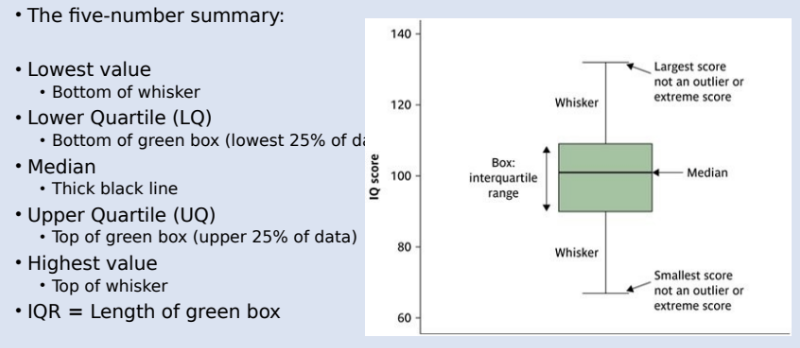
2. Interquartile Range (IQR):

   • Scores between the 25th and 75th percentiles, excluding extremes.

3. Variance:

   • Average squared deviation from the mean; uses information from all scores.

4. Standard Deviation (SD):

   • Square root of variance; indicates average deviation from the mean.

Page 31: Boxplots Overview

Page 37: Standard Deviation Calculation & Importance

• most commonly used measure of spread

• Square root of variance; puts variance back into the original scale/values measured

Page 38: Understanding SD Clusters

• If the SD is large, the data are dispersed

• If the SD is small, the data are more clustered around the mean

Page 39: Describing a Data Set

• Discuss changes in understanding dataset with key metrics: data points count, max/min ranges, central tendency.

Page 43: Impact of Measurement Levels on Descriptive Statistics

• Descriptive statistics change according to level of measurement

  • Nominal data = frequency

  • Ordinal data = frequency, mode, median

  • Interval/ratio = mean, SD

Page 45: Key Terms for Learning

• Descriptive statistics

• Inferential statistics

• Nominal/categorical

• Ordinal

• Interval

• Ratio

• Central tendency

• Spread/dispersion

• Mean

• Median

• Mode

• Range

• Inter-quartile range

• Variance

• Standard deviation

• ∑

• N