Chapter 2: Kinematics

Position

Before describing the motion of an object, we must first
define its position.
The position of an object is its location relative to a
convenient reference frame.
A reference frame is where and how we set up a system of axes in relation to which measurements can be made.
Common reference frames include the Earth or you.
Most of the time, we choose a stationary reference frame, but there are situations in which we choose a moving reference frame.
This is dependent on the problem.

Displacement

Displacement is the change in position of an object.
The displacement is defined as ∆𝑥 = 𝑥𝑓 − 𝑥0
- ∆𝑥 is the displacement
- 𝑥𝑓 is the object’s final position
- 𝑥0 is the object’s initial position
The Greek letter ∆(delta) always means “a change in” whatever quantity follows.
∆x means “a change in position.”
The SI unit of displacement is the meter.
If other units are given, the displacement may need to be converted into meters.

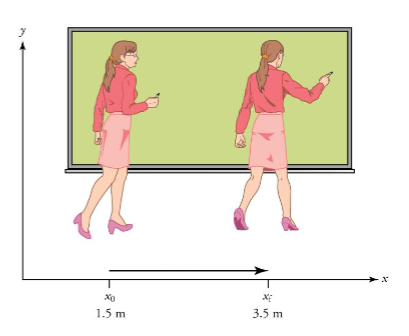
Practice Problem 1

A professor stands 1.5 m away from the left edge of a blackboard. If she moves to 3.5 m away from the left edge of the blackboard, what is her displacement?

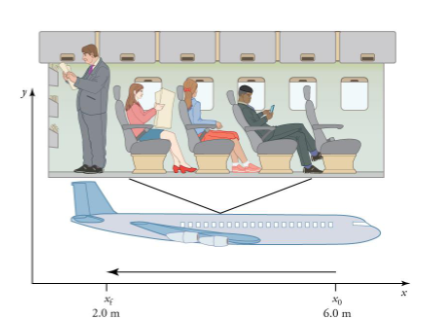
Practice Problem 2

A passenger sits in his seat 6.0 m from the back edge of a plane. The passenger stands up and moves toward the back of the plane until he is 2.0 m away from the back edge. What is his displacement?

∆x = xf - x0

∆x = 2.0m - 6.0m = -4.0m

Notice that displacement can be positive or negative.
The number represents the magnitude or the amount.
The positive or negative sign indicates the direction.
Displacement has both a magnitude and a direction.

Distance

Distance is not the same as displacement.
Displacement has a direction, but distance does not.
Distance is the magnitude of displacement; it does not have a direction.

Distance Traveled

Displacement is the change in position between two points. It does not depend on the path traveled and only cares about the starting position and the final position.
Distance is the magnitude of the displacement.
Distance traveled is the total length of the path between two positions. This does depend on the path traveled.

Practice Problem 3

A cyclist rides 3 km west and then turns around and rides 2 km east.
(a) What is her displacement?
(b) What is the total distance that she traveled?
(c) What is the magnitude of her displacement?

Scalars and Vectors

A scalar is a quantity defined only by a magnitude.
Scalars include quantities such as distance, temperature and speed.
A vector is a quantity with both a magnitude and a direction.
Vectors include quantities such as displacement, velocity and force.

Coordinate Systems for 1D Motion

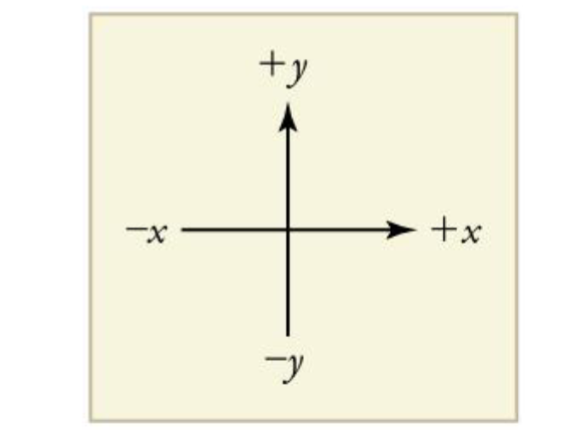
In order to describe the direction of a vector quantity, we must designate a coordinate system within the reference frame.
For 1D Motion, this is usually a vertical line or
a horizontal line.
For a vertical line, up is usually positive and down is negative.
For a horizontal line, right is usually positive and left is negative.

Practice Problem 4

A person’s speed can stay the same as he or she rounds a corner and changes direction. Given this information, is speed a scalar or a vector
quantity? Explain.

Scalar

Time

In addition to knowing the change in position of an object, it is often important to know how long it took for that change in position to occur.
The SI units of time are seconds (s).
The elapsed time is defined as ∆𝑡 = 𝑡𝑓 − 𝑡0
- ∆𝑡 is the elapsed time.
- 𝑡𝑓 is the time at the end of the motion.
- 𝑡0 is the time at the start of the motion.

Velocity

The average velocity of an object is defined as the change in
position divided by the elapsed time.
v = ∆𝑥/∆𝑡 = 𝑥𝑓 − 𝑥0/𝑡𝑓 − 𝑡0
where v is the velocity of the object.

For most problems, 𝑡0 will be set to 0, so the velocity equation can be simplified to v = ∆𝑥/𝑡

Instantaneous Velocity

The instantaneous velocity, v, is the average velocity at a specific instant in time.
This is done by taking an infinitesimal change in displacement and dividing by the infinitesimal change in time.
Solving this mathematically requires calculus and is beyond the scope of this class.

Practice Problem 5

A new European record for the 100-meter dash was set during the Tokyo Olympics. Lamont Marcell Jacobs ran the 100-meter dash in 9.80 s. What was his average velocity during this event?

Practice Problem 6

The distance from Laredo to Austin is 379 km. If the total time for the trip is 3 hours and 40 minutes, what is the average velocity during this
trip in
(a) km/hr and
(b) m/s?

Practice Problem 7

A person leaves home and travels 4 km west on their bicycle. Then, they turn around and travel 2 km back east before stopping. What was their average velocity for this trip?

Speed

In everyday life, we interchange the words speed and velocity.
In physics, these are different quantities.
Velocity is a vector and speed is a scalar.

Instantaneous Speed

The instantaneous speed is the magnitude of the instantaneous velocity.
If the instantaneous velocity is -3.0 m/s, then the instantaneous speed is 3.0 m/s.
Note that the speed is always a positive number as it is just a scalar.

Average Speed

The average speed is the distance traveled divided by the elapsed time.
This is different from velocity, which is displacement divided by
the elapsed time.

Velocity Versus Speed (sc)

Acceleration

In everyday conversation, acceleration means to speed things up.
In physics, the acceleration is the change in velocity over the change in time or
a = ∆𝑣/∆𝑡 = 𝑣𝑓 − 𝑣0/𝑡𝑓 − 𝑡0
Like velocity, acceleration is also a vector, which means it can be positive or negative.
Since velocity is a vector, Δv can be either a change in magnitude or a change in direction.
This means that acceleration is a change in direction, speed or both.

Deceleration and Negative Acceleration

Deceleration always refers to acceleration in the opposite direction of the direction of motion.
Deceleration always reduces the speed of an object.
Negative acceleration is acceleration in the negative direction of the coordinate system.
Remember, the positive or negative sign indicates the direction.