PY 131 Chapter 10: Projectile Motion

Motion in Multiple Dimensions

• We previously discussed motion in 1 dimension i.e. along a line.

• But the universe has 3 dimensions so how do we describe motion in more than one dimension?

• As before, the first thing we have to do is choose set up a coordinate system now with 3 axes (usually x,y,z).

  

• Now consider an object in 3D space. At time t1 it has coordinates x1 , y1 , z1 : at time t2 it has coordinates x2 , y2 , z2 .

  

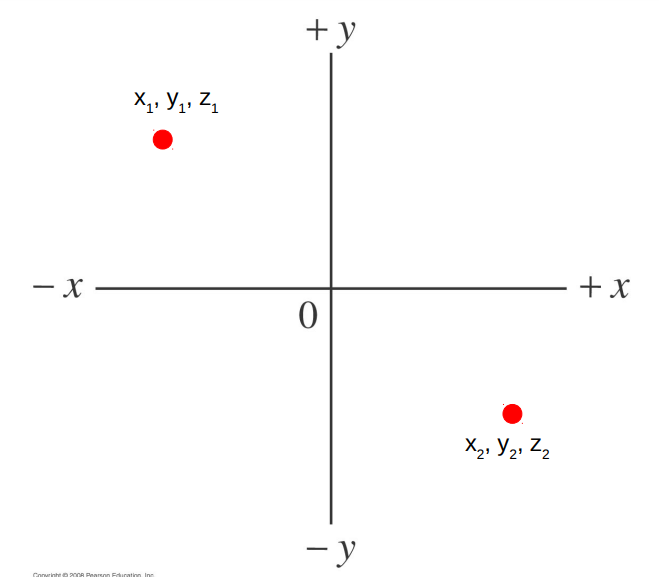
• We can define an average velocity, v x , v y , v z .

  

• As with motion in 1D, as the time interval becomes smaller and smaller, the average velocity becomes the instantaneous velocity.

• The speed v is found by Pythagorean Theorem

  

• At time t1 the object has a velocity, vx1, vy1, vz1, at time t2 the object has a velocity, vx2, vy2, vz2.

• We can define an average acceleration, a x , a y , a z .

  

• As the time interval becomes smaller and smaller, the average acceleration becomes the instantaneous acceleration.

• The motion of an object along each coordinate is independent!

  • What is going on in the x direction is independent of what is going on in the y direction which is independent of what is going on in the z direction.

• For example, an object can be accelerating along one coordinate but have no acceleration along another.

• Newton’s Laws apply to each coordinate separately!

• For example, if there is a net force in the x direction then the acceleration in the x direction is

  • ax = Fnet x / m

• If there is a net force in the y direction then the acceleration in the y direction is

  • ay = Fnet y / m

Projectile Motion

• Motion in two (or more) dimensions under the influence of gravity is called Projectile Motion.

• Most often the x-axis is horizontal, the y-axis vertical up.

  • It doesn’t have to be, you can pick anything you want, horizontal and vertical makes the problem easier.

• The motion can be broken up into the motion in the x direction (horizontal), and the motion in the y direction (vertical).

• Gravity points down so the force on an object is -mg. There is no force in the x direction.

• The acceleration in the x direction is zero, the only non-zero acceleration is a_y = -g.

• Consider a ball rolling along a table and reaching the edge.

  

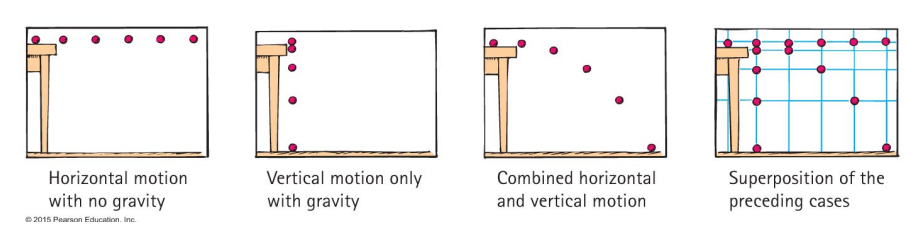
• Just as it reaches the edge the ball has a non-zero x velocity but zero y velocity.

• Since there is no x acceleration, the ball keeps the same x velocity.

• The ball does have acceleration in the y direction, -g, so it starts to fall and pick up y velocity at a rate of 10 m/s/s.

• The motion of the ball is the combination of the horizontal and vertical motions.

• These two objects will hit the ground at the same time.

• Consider a ball that is thrown at some angle. Now the ball has non-zero velocity in the x and y direction.

  

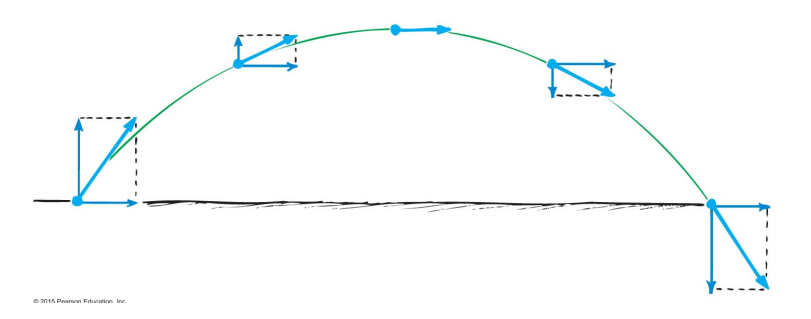
• As before, there is no x acceleration so the ball keeps the same x velocity.

• The ball does have acceleration in the y direction, -g, so initially its y velocity decreases to zero and then it starts to increase in the downward direction.

• The motion of the ball is the combination of the horizontal and vertical motions.

• Consider a ball that is thrown such that its initial horizontal velocity is 40 m/s and its initial vertical velocity is 30 m/s.

  • The initial speed = √( (30 m/s)2 + (40 m/s)2) = 50 m/s
  • At t = 1 s the ball has a horizontal velocity of 40 m/s and a vertical velocity of 20 m/s.
  • The average vertical velocity is 25 m/s. The ball travels 40 m horizontally, 25 m up from t = 0 to t = 1 s. At t = 2 s the ball has a horizontal velocity of 40 m/s and a vertical velocity of 10 m/s.
  • The average vertical velocity is 15 m/s.

• The ball travels 40 m horizontally, 15 m up from t = 1 s to t = 2 s.

  • Totals are 80 m horizontally, 40 m up

• At t = 3 s the ball has a horizontal velocity of 40 m/s and a vertical velocity of 0 m/s.

  • The average vertical velocity is 5 m/s.

• The ball travels 40 m horizontally, 5 m up from t = 2 s to t = 3 s.

  • Totals are 120 m horizontally, 45 m up

• At t = 4 s the ball has a horizontal velocity of 40 m/s and a vertical velocity of -10 m/s.

  • The average vertical velocity is -5 m/s.

• The ball travels 40 m horizontally, 5 m down from t = 3 s to t = 4 s.

  • Totals are 160 m horizontally, 40 m up

• At t = 5 s the ball has a horizontal velocity of 40 m/s and a vertical velocity of -20 m/s.

  • The average vertical velocity is -15 m/s.

• The ball travels 40 m horizontally, 15 m down from t = 4 s to t = 5 s.

  • Totals are 200 m horizontally, 25 m up

• At t = 6 s the ball has a horizontal velocity of 40 m/s and a vertical velocity of -30 m/s.

  • The average vertical velocity is -25 m/s.

• The ball travels 40 m horizontally, 25 m down from t = 5 s to t = 6 s.

  • Totals are 240 m horizontally, 0 m up i.e. ground level again.

• The ball spent 6 seconds in the air and traveled 240 horizontally.

QUESTION 1:

What determines how long the ball spends in the air?

• ==The initial velocity in the y direction.==
• The larger the initial velocity in the y direction, the higher the ball goes, the longer it will spend in the air.

QUESTION 2:

• A battleship simultaneously fires two shells with the same initial velocity at two submarines. The trajectories of the shells are shown. Which submarine is hit first?

  

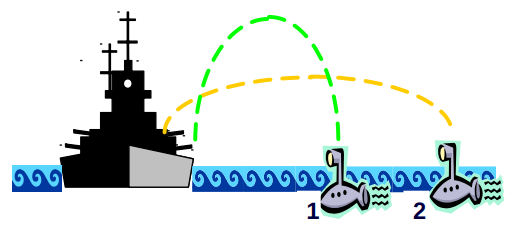
Since the initial velocity of both shells is the same, the shell that hits the submarine first is the one that has a shorter distance to travel. Looking at the trajectories of the shells, shell 2 has a shallower curve and a longer horizontal distance to cover. On the other hand, shell 1 has a steeper curve and a shorter horizontal distance to cover. ==Therefore, shell 1 will hit the submarine first.==

QUESTION 3:

The trajectories of three punts are shown. Which has the longest hang time?

• ==1 will have the longest hang time==

QUESTION 4:

Ashley and Brian are standing on top of a tall building each holding a golf ball. At the same time, Brian drops his ball off the edge while Ashley throws hers off horizontally. Whose golf ball hits the ground first?

• ==They hit at the same time==

What determines how long the ball travels horizontally?

• ==The distance traveled horizontally is determined by the x velocity and the time spent in the air.==

The Range

• The distance a projectile travels horizontally is called its range.
• Ignoring air resistance then for a given initial speed, the launch angle which maximizes the range is 45 degrees.
• 
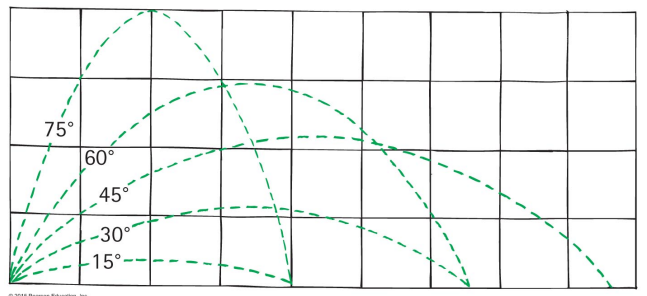
• Launch angles θ less than 45 degrees will have a range equal to the case where the launch angle is 90 – θ.
• With air resistance, the range is more complicated to determine because it depends on the size and mass of the object.
  • Air resistance leads to an acceleration in the x direction.
• The general trend is that the longest range for an object occurs for launch angles less than 45 degrees.
  • Sometimes it’s a lot less than 45: the optimal launch angle for a golf ball is around 40 degrees, for a baseball it is more like 30 degrees.

\