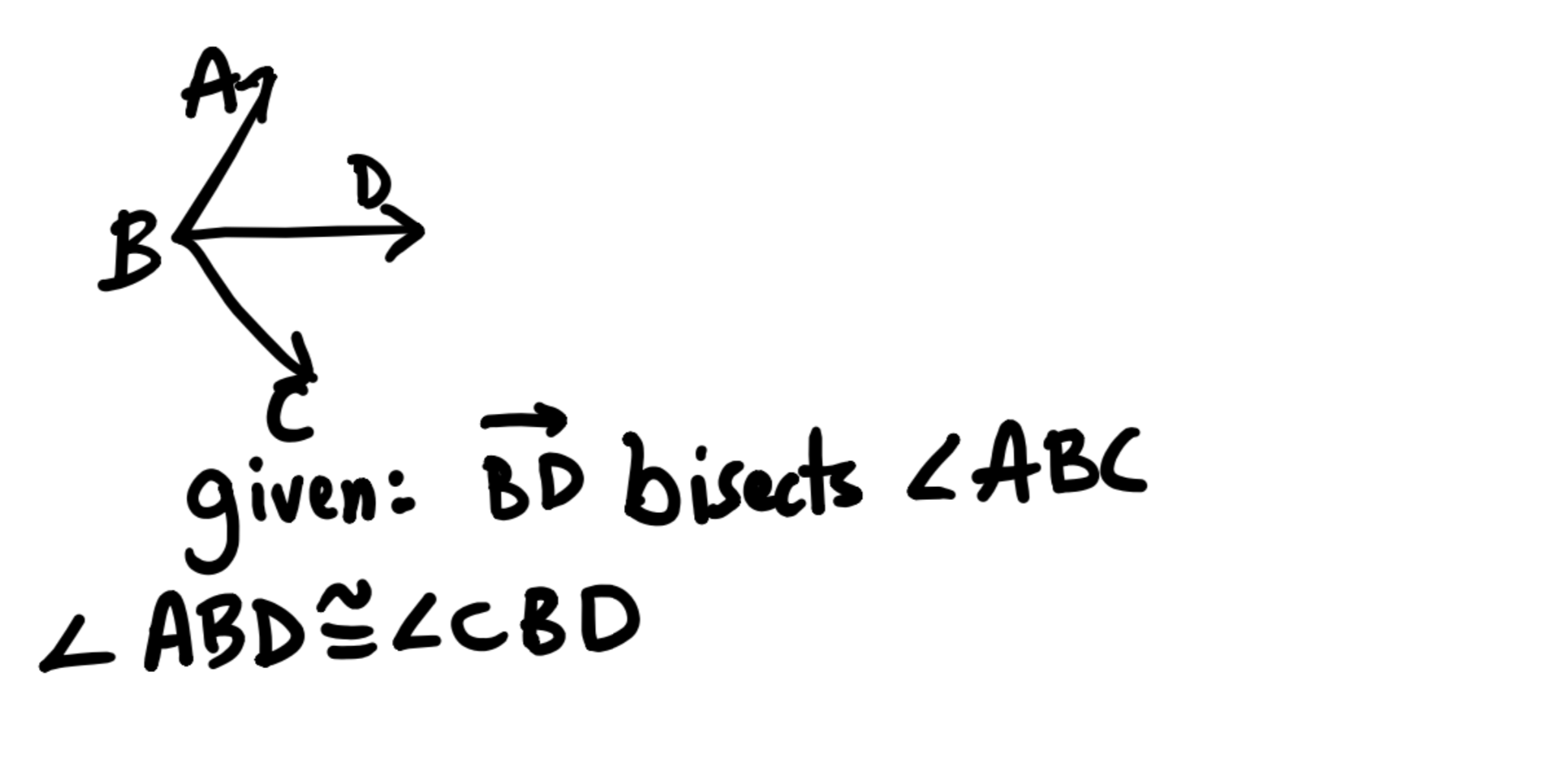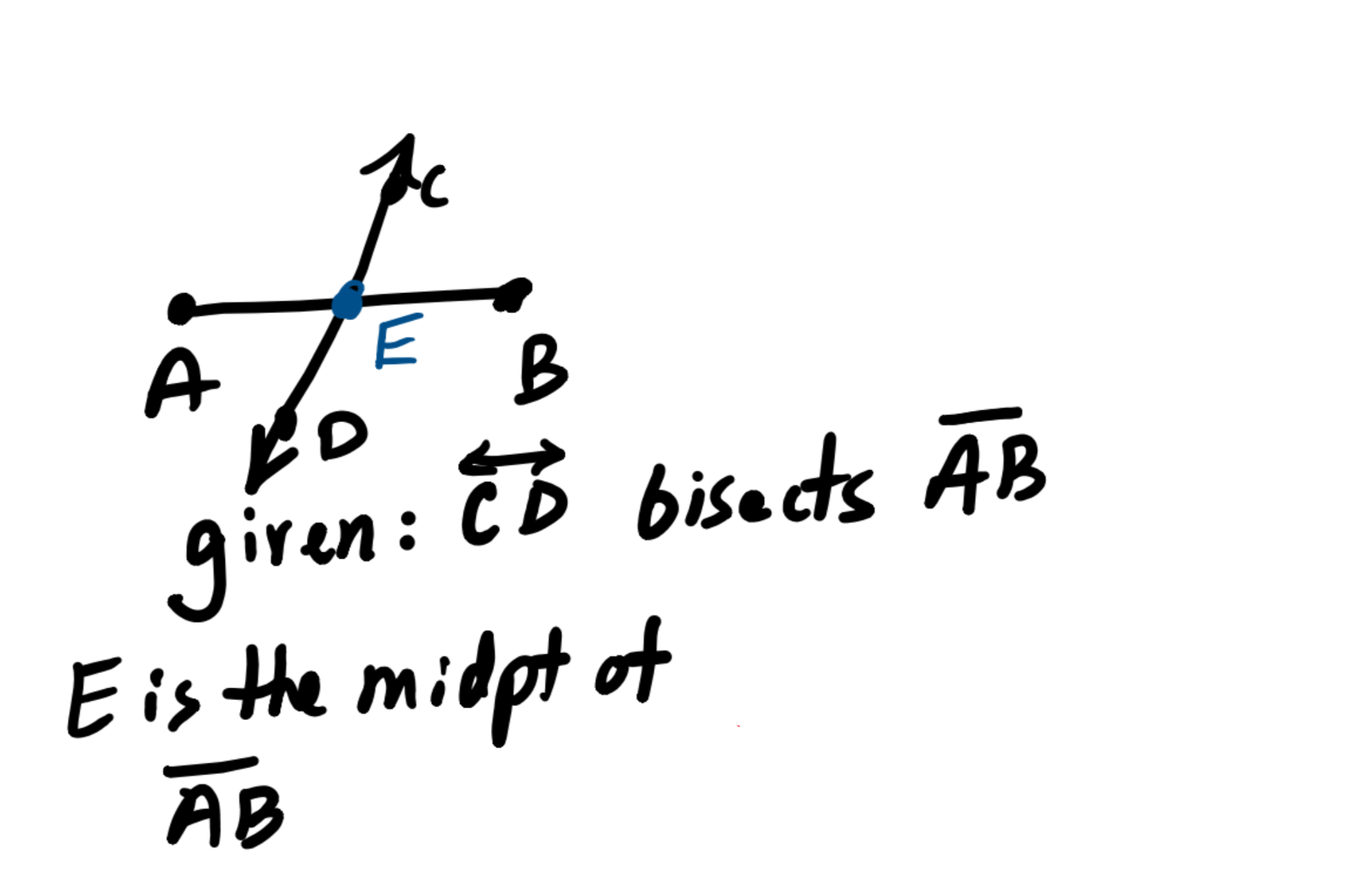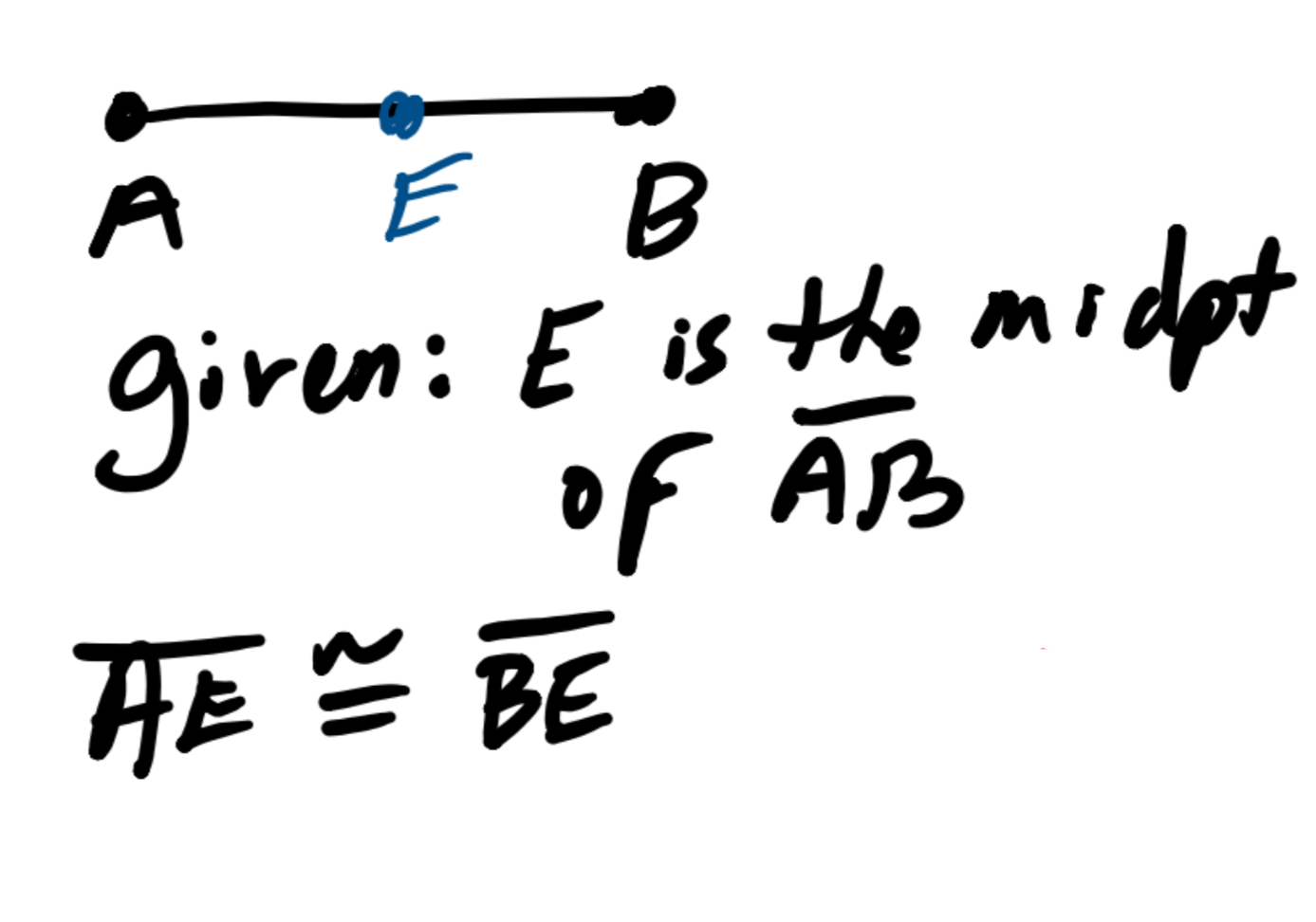Proofs
Notice: these are modified version of notes provided in class by a teacher.
Proofs - ways to state/prove a conclusion is true based on given information, properties, postulates and theorems.
Properties
Property | Example |
|---|---|
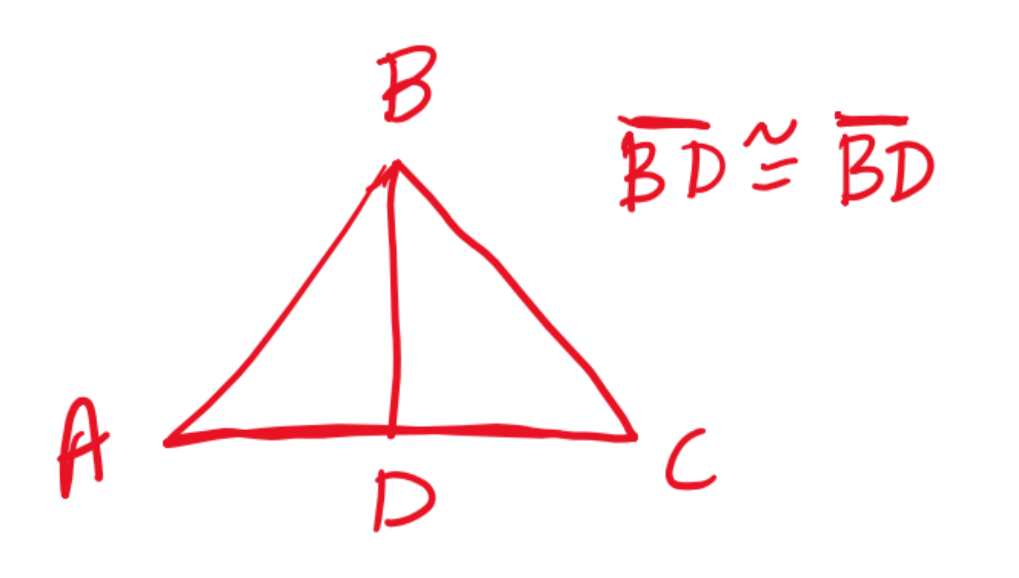
Reflexive property - identical angles, lines, etc are congruent to each other. |
|
Transitive Property - congruency “transfers” | if ∠A ≅ ∠P and ∠P ≅ ∠T then ∠A ≅ ∠T |
Postulates/Theorems
Postulate/Theorem | Example |
|---|---|
pythagorean theorem | |
isosceles triangle theorem | |
3rd angle theorem | The Third Angle Theorem states that if two angles in one triangle are congruent to two angles in another triangle, then the third pair of angles must also be congruent
Why? - because all triangles have to add up to 180°. |
Transversal Properties If two parallel lines are cut by a transversal, then:
|
|
Vertical Angles are always congruent |
Definitions
Definition | Example |
|---|---|
Definition of an angle bisector |
|
Definition of a segment bisector |
|
Definition of a midpoint |
|
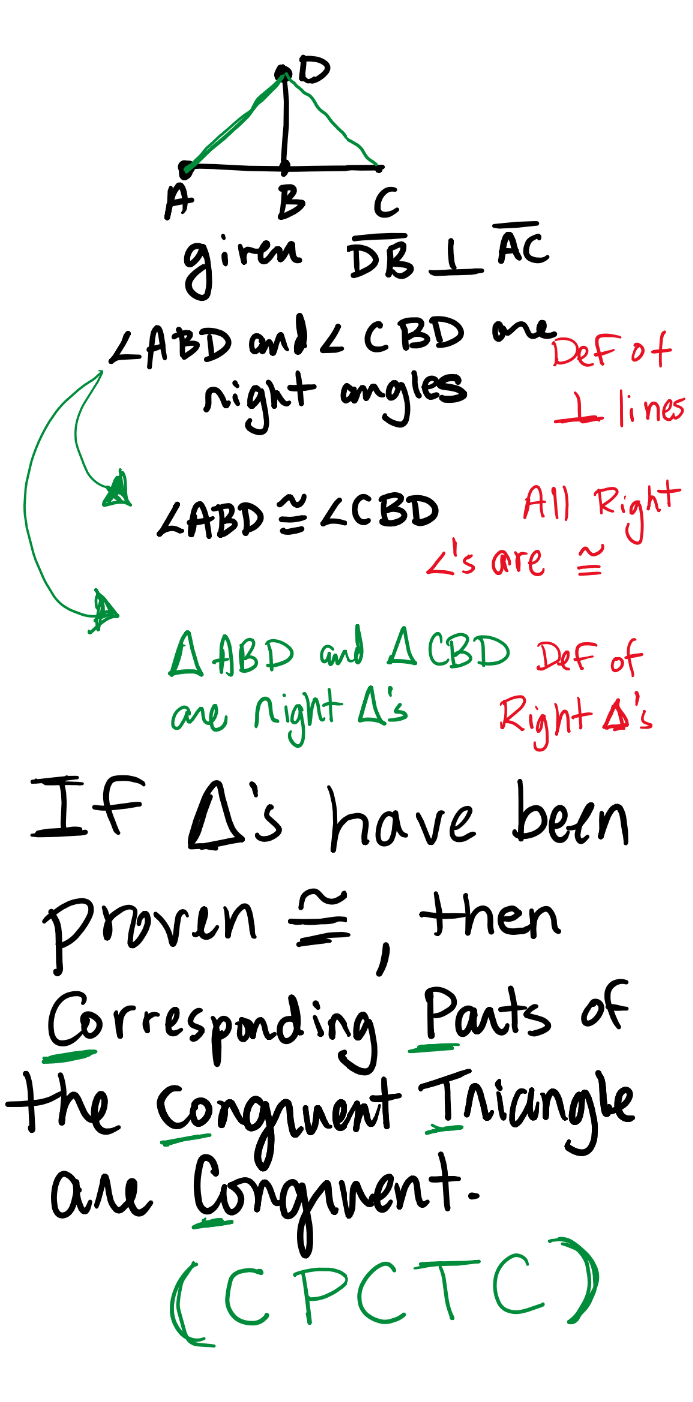
Definition of perpendicular lines |
|
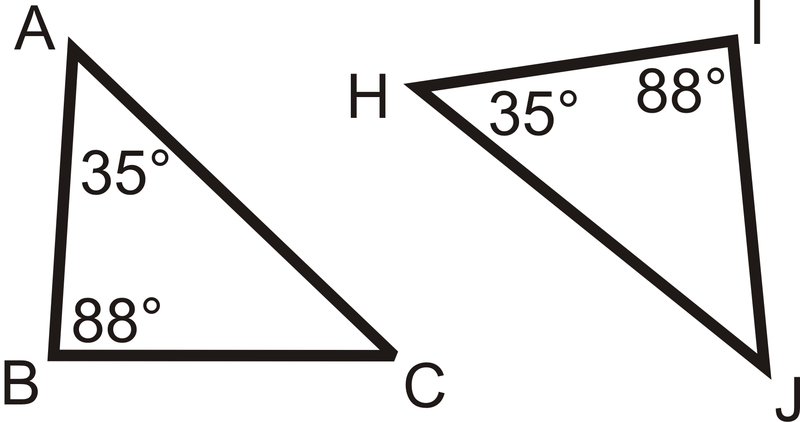 ∠C and ∠J are congruent because all the others are congruent.
∠C and ∠J are congruent because all the others are congruent.