Introduction to Limits
It is simply a point in anything that should not be exceeded. If we approximate “x” close enough to a number “a” (without being a) on both left and right sides, f(x) approximates a number “L”, then the limit when x tends to a is L:
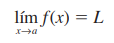
The limit of a function at a point x subzero is the value that the “y”s approach when the values at “x” approach the value x subzero.
For example, the limit of f(x) = x2 - 9 / x - 3 when x tends to 3, x will have approximate values of 3 but never 3, if we evaluate in y it will have approximate values of 6 from the right and from the left but never 6**.**
We can evaluate functions from the right (+) or from the left(-), these are called one-sided limits.
For example, if we evaluate this function:
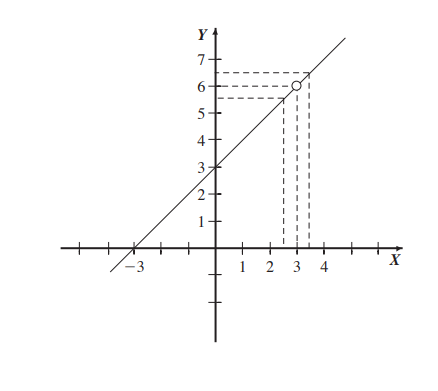
If we evaluate when x tends to 3+ (from the right) and when x tends to 3- (from the left) our limit is 6.
There will be cases like this:
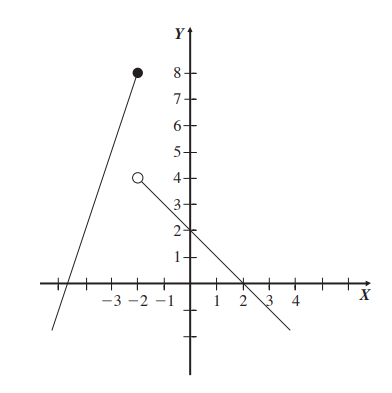
If we evaluate when x tends to -2+ (from the right), our limit is 4, and when x tends to -2- (from the left) our limit is 8, we have different values, therefore the limit doesn’t exist.
Tips
First, locate your x and from there search when the function or functions go through that x and evaluate from your left and then your right in y.
In rational functions, their graphic is asymptotes in that case limits aren’t defined because they tend to be ∞ or -∞ but that doesn´t mean they don’t exist.