Physiology 2

osmosis:: the diffusion of water across a semipermeable membrane up a solute concentration gradient

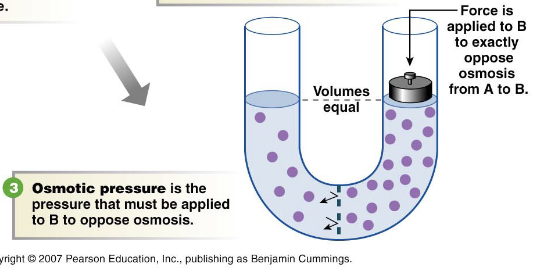osmotic pressure diagram osmosis depends on:: the number of particles in a given volume of solution

osmolarity:: = molarity * particles/molecule

hyperosmotic:: higher osmolarity in relation to another solution

hypoosmotic:: lower osmolarity in relation to another solution

isosmotic:: the same osmolarity in relation to another solution

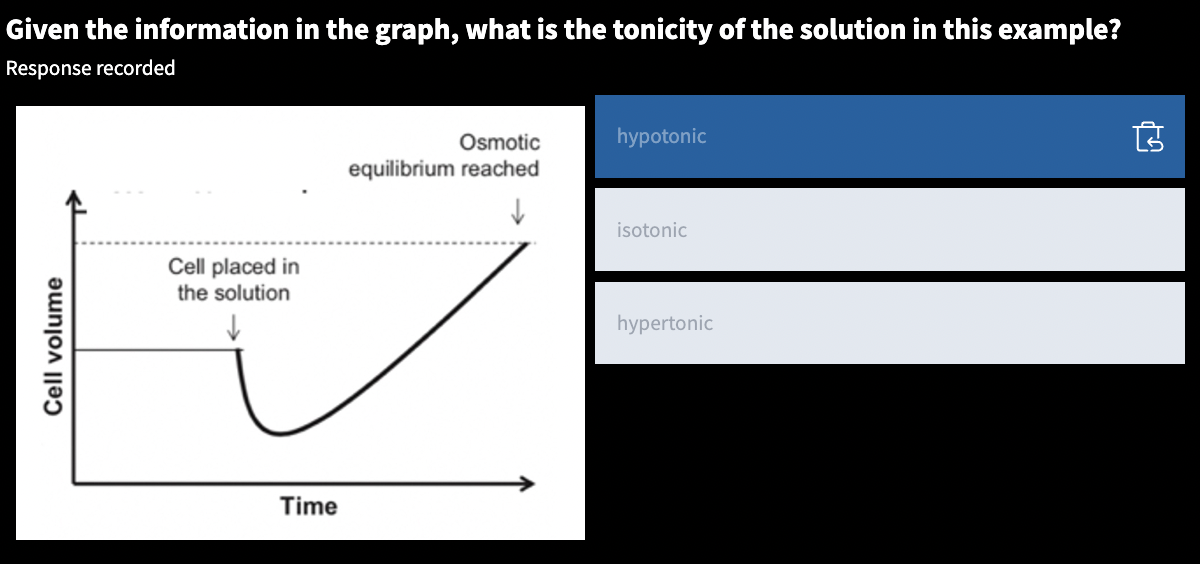
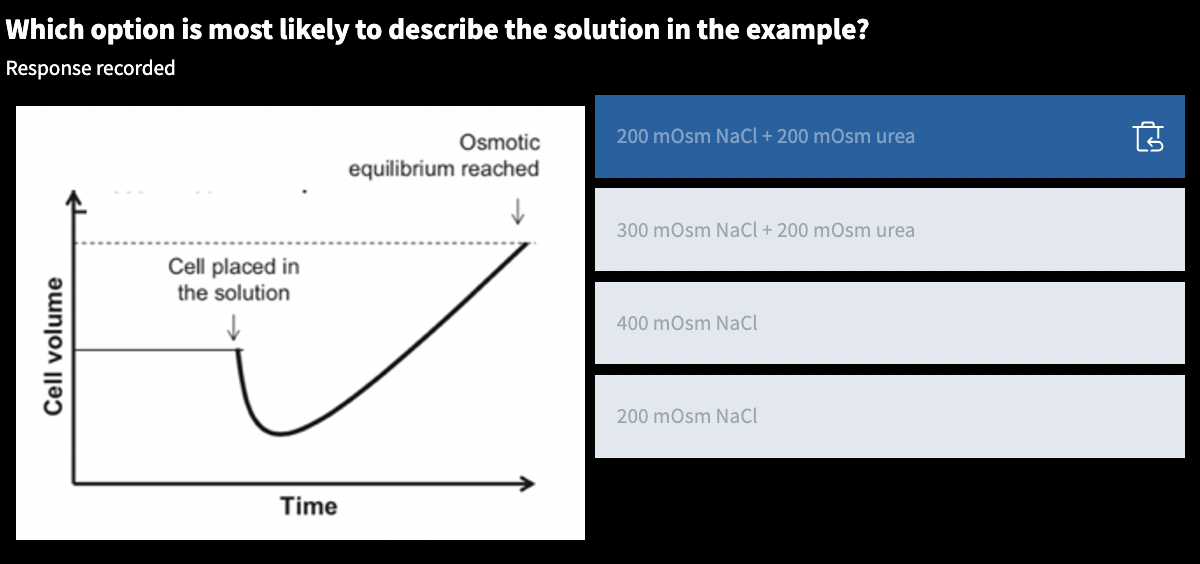
tonicity:: describes a solution based on its effects on the volume of a cell placed in the solution

hypertonic:: water diffuses out, shrinking

hypotonic:: water diffuses in, swelling

lysis:: a very hypotonic solution causes _____

isotonic:: water diffuses normally, no effect to the cell

nonpenetrating solutes:: only solutes that effect osmolarity and tonicity

osmolarity and tonicity rules

Correct answer: C because mOsm=mM

body fluid osmolarity:: 300 mOsm

Correct answer: A because, though the osmolarity of the solutions is the same, the outside solute contains only part nonpenetrating solutes, thus the osmolarity of nonpenetrating solutes is less than that of the cell and water must enter the cell to decrease its solute concentration. The solution is hypotonic to the cell nonpenetrating:: assume that all intracellular solutes are _____

Correct answer: A because equilibrium is reached by the cell volume increasing

Correct answer: A because volume fluctuates (has to have penetrating component) and mOsm of nonpenetrating solute has to be lower than 300 mOsm

Knowt

4.0(1)

Generate Practice test

Chat with Kai

undefined Flashcards

0 Cards0.0(0)