
Resumo Prova 1 - Matemática Discreta
Erros e Representação de Números
Arredondamento:
Última casa considerada deve sofrer um acréscimo se a primeira casa eliminada for um número igual ou maior que cinco
Exemplos (4 casas decimais):
325,598678 = 325,5987
-251,256897 = -251,2569
0,24955 = 0,250
Truncamento:
Considera-se um certo número de casas após a vírgula e as que veem depois dessas são eliminadas sem qualquer alteração nas que ficaram
Exemplos (4 casas decimais):
325,598678 = 325,5986
-251,256897 = -251,2568
0,24955 = 0,2495
Ponto Flutuante:
Números reais, pequenos ou grandes, são escritos no sistema de ponto flutuante
Forma: ±0, d1d2d3 … dn x bexp
Componentes:
Mantissa: ±0, d1d2d3 … dn
Expoente: exp
Base: b
Exemplo:
38,729 = 0,38729 × 10²
Mantissa = 0,38729
Expoente = 2
Base = 10
Outros exemplos:
12542,78587 = 0,1254278587 × 105
0,002356 = 0,2356 × 10−2
Número para a direita o expoente aumenta
Número para a esquerda o expoente diminui
Operações com ponto flutuante:
𝑥 = 0,287 × 105
𝑦 = 0,2734 × 103
𝑥 + 𝑦 = 0,287 × 105 + 0,002734 × 105 = 0,289734 × 105
Pega o menor expoente (3) e converte para o maior (5)
𝑥 ∙ 𝑦 = 0,287 × 105 × 0,2734 × 103 = 0,0784658 × 108
Só mantém a base e soma os expoentes
Conversão de bases:
Decimal para binário:
1010.01 = 10,25
Valores de cada bit:
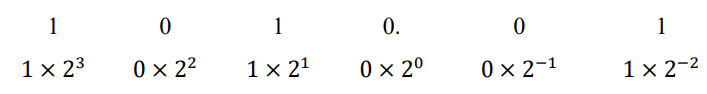
8 + 0 + 2 + 0 + 0 + 0,25 = 10,25
Decimal para binário:
25 = 11001
Equação:
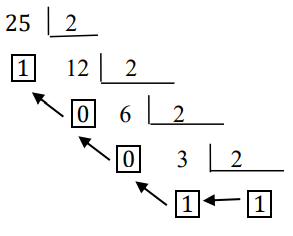
25,1875 = 11001.0011
Conversão da parte decimal:
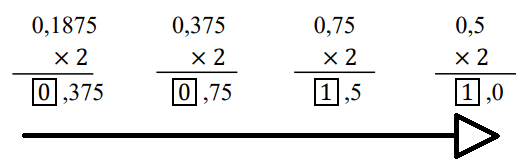
Binária em ponto flutuante:
Conversão do número 50:
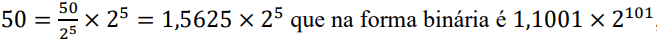
25 foi escolhido pois é a potência de 2 que mais se aproxima de 50 sem ultrapassar
Armazenamento de número na memória do computador:
Na precisão dupla os números são armazenados em uma cadeia de 64 bits
Exemplo:

Teoria dos Conjuntos
Representação:
A = {a,e,i,o,u} → Por elementos
A = {x | x é vogal} → Pela propriedade
Digrama de Venn:
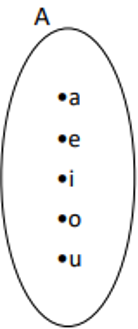
Pertinência:
a ∈ A → elemento “a” pertence ao conjunto “A“
a ∉ A → elemento “a” não pertence ao conjunto “A“
Tipos:
Vazio:
Não tem elementos
Representado por {} ou ∅
Unitário:
Somente um elemento
Universo:
Representado por U
Contém todos os conjuntos de um determinado contexto
Conjuntos numéricos:
Explicação:

Subconjunto:
Explicação:


Operações com conjuntos:
Explicação:


Produto cartesiano:
Explicação:


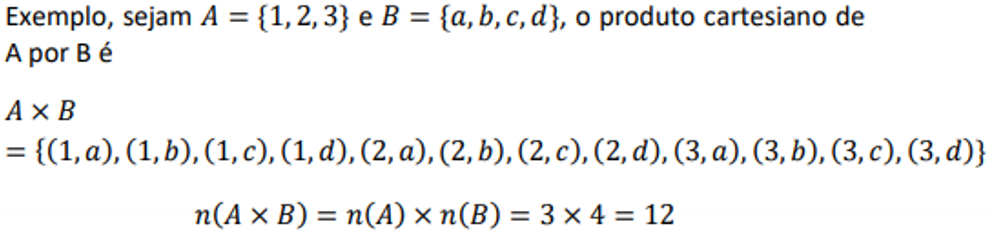
Relações e Funções
Relação:
Relação é uma comparação entre dois objetos
Estes objetos estão ou não relacionados de acordo com alguma regra
Uma relação é um conjunto de pares ordenados
Domínio e imagem:
O domínio (D) é o conjunto de todos os primeiros elementos de um par ordenado
Imagem (Im) é o conjunto dos segundos elementos
Exemplo:
𝑅 = {(1, 𝑦), (1, 𝑧), (3, 𝑦)}
D(R) = {1, 3}
Im(R) = {y, z}
Representações:
𝐴 = {1, 2, 3} , 𝐵 = {𝑥, 𝑦, 𝑧} e seja 𝑅 = {(1, 𝑦), (1, 𝑧), (3, 𝑦)}
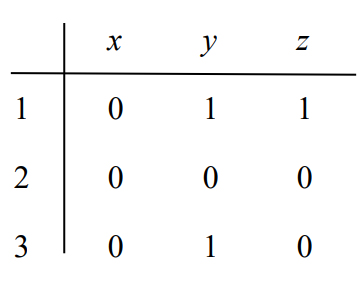
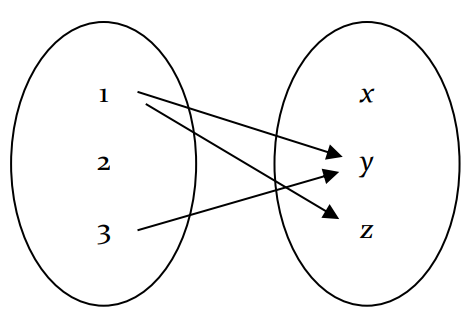
𝐴 = {1, 2, 3,4} e seja 𝑅 = {(1, 2), (2, 2), (2, 4), (3, 2), (3, 4), (4, 1), (4, 3)}
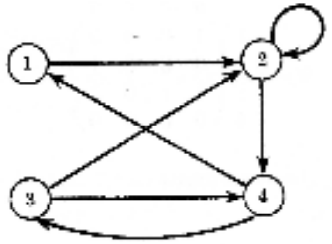
Função:
Toda função é uma relação
Transforma elementos de um conjunto origem em elementos de um conjunto saída
“CADA ELEMENTO DE UM CONJUNTO DE ENTRADAS DEVE ESTAR RELACIONADO A UM ÚNICO ELEMENTO DO CONJUNTO DE SAÍDAS”
Se não seguir a regra acima a relação não é função
Tipos:
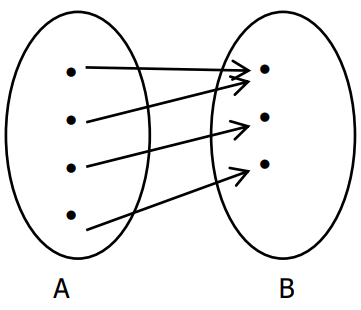
Injetora:
Não há elemento em B com mais de um componente em A
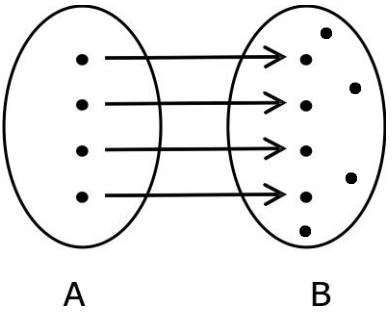
Sobrejetora:
Qualquer elemento de B é imagem de, pelo menos, um elemento de A
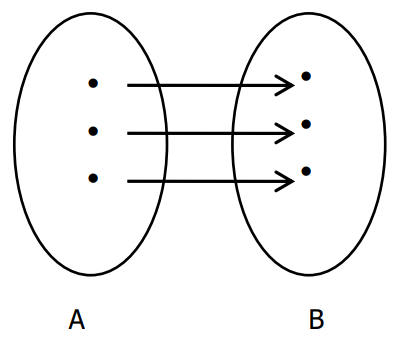
Bijetora:
Se ela for injetora e sobrejetora
Função inversa:
A inversa de uma função f pode ser denotada por f-1
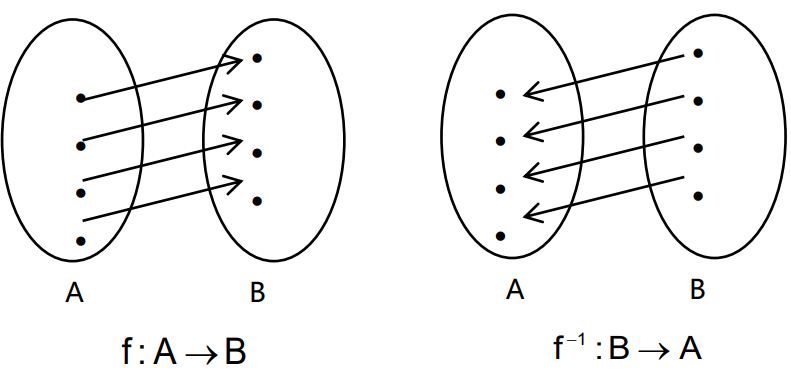
Para encontrar a inversa, deve-se trocar x por y
Exemplos:
f(x) = x + 5
y = x + 5
x = y + 5
x - 5 = y
f(x) = 2x – 3
y = 2x - 3
x = 2y - 3
x + 3 = 2y
x/2 + 3/2 = y
Função composta:
Genericamente, escrevemos h(x) = g(f(x)) ou (g ○ f)(x)
Exemplo:
f(x) = 2x + 2
g(x) = 5x
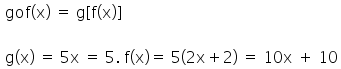
Função valor inteiro:
INT(x) converte x em um inteiro apagando a parte fracionária
Exemplos:
INT (42,98) = 42
INT (-42,98) = -42
INT (42) = 42
INT (-42) = -42
Função valor absoluto:
É o maior dos valores entre x e –x
ABS(x) ou |x|
Exemplos:
|-72,53| = 72,53
|72,53| = 72,53
Função floor:
Definição:
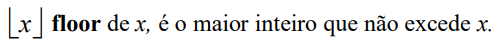
Exemplos:
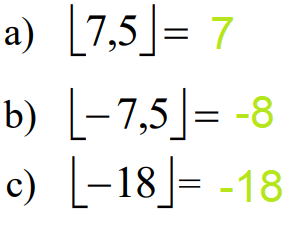
Função ceiling:
Definição:
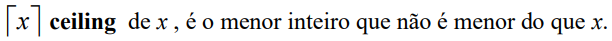
Exemplos:
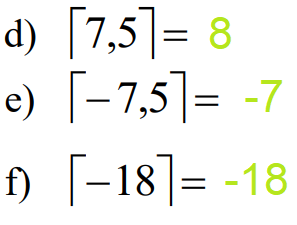
Função resto:
Seja k inteiro qualquer e M positivo, então k(modM)
Se k é negativo divida k por M para obter o resto r:
k (modM)=M-r
Exemplos:

Resumo Prova 1 - Matemática Discreta
Erros e Representação de Números
Arredondamento:
Última casa considerada deve sofrer um acréscimo se a primeira casa eliminada for um número igual ou maior que cinco
Exemplos (4 casas decimais):
325,598678 = 325,5987
-251,256897 = -251,2569
0,24955 = 0,250
Truncamento:
Considera-se um certo número de casas após a vírgula e as que veem depois dessas são eliminadas sem qualquer alteração nas que ficaram
Exemplos (4 casas decimais):
325,598678 = 325,5986
-251,256897 = -251,2568
0,24955 = 0,2495
Ponto Flutuante:
Números reais, pequenos ou grandes, são escritos no sistema de ponto flutuante
Forma: ±0, d1d2d3 … dn x bexp
Componentes:
Mantissa: ±0, d1d2d3 … dn
Expoente: exp
Base: b
Exemplo:
38,729 = 0,38729 × 10²
Mantissa = 0,38729
Expoente = 2
Base = 10
Outros exemplos:
12542,78587 = 0,1254278587 × 105
0,002356 = 0,2356 × 10−2
Número para a direita o expoente aumenta
Número para a esquerda o expoente diminui
Operações com ponto flutuante:
𝑥 = 0,287 × 105
𝑦 = 0,2734 × 103
𝑥 + 𝑦 = 0,287 × 105 + 0,002734 × 105 = 0,289734 × 105
Pega o menor expoente (3) e converte para o maior (5)
𝑥 ∙ 𝑦 = 0,287 × 105 × 0,2734 × 103 = 0,0784658 × 108
Só mantém a base e soma os expoentes
Conversão de bases:
Decimal para binário:
1010.01 = 10,25
Valores de cada bit:
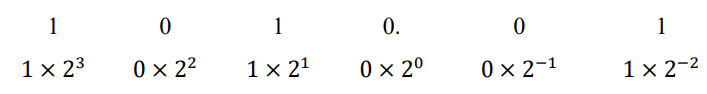
8 + 0 + 2 + 0 + 0 + 0,25 = 10,25
Decimal para binário:
25 = 11001
Equação:

25,1875 = 11001.0011
Conversão da parte decimal:
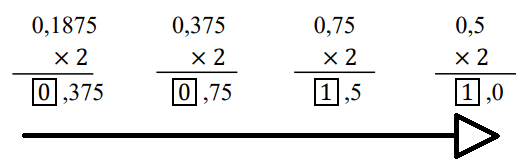
Binária em ponto flutuante:
Conversão do número 50:
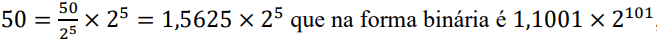
25 foi escolhido pois é a potência de 2 que mais se aproxima de 50 sem ultrapassar
Armazenamento de número na memória do computador:
Na precisão dupla os números são armazenados em uma cadeia de 64 bits
Exemplo:

Teoria dos Conjuntos
Representação:
A = {a,e,i,o,u} → Por elementos
A = {x | x é vogal} → Pela propriedade
Digrama de Venn:

Pertinência:
a ∈ A → elemento “a” pertence ao conjunto “A“
a ∉ A → elemento “a” não pertence ao conjunto “A“
Tipos:
Vazio:
Não tem elementos
Representado por {} ou ∅
Unitário:
Somente um elemento
Universo:
Representado por U
Contém todos os conjuntos de um determinado contexto
Conjuntos numéricos:
Explicação:

Subconjunto:
Explicação:


Operações com conjuntos:
Explicação:


Produto cartesiano:
Explicação:


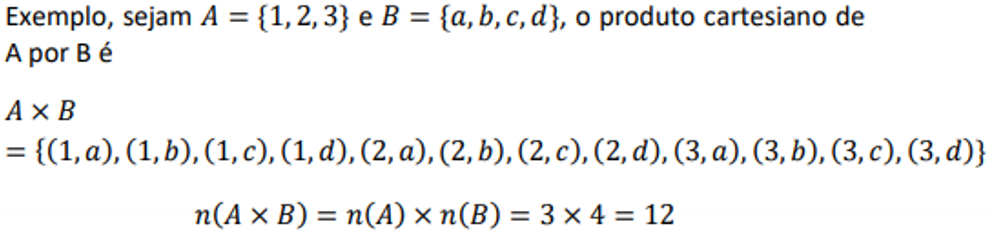
Relações e Funções
Relação:
Relação é uma comparação entre dois objetos
Estes objetos estão ou não relacionados de acordo com alguma regra
Uma relação é um conjunto de pares ordenados
Domínio e imagem:
O domínio (D) é o conjunto de todos os primeiros elementos de um par ordenado
Imagem (Im) é o conjunto dos segundos elementos
Exemplo:
𝑅 = {(1, 𝑦), (1, 𝑧), (3, 𝑦)}
D(R) = {1, 3}
Im(R) = {y, z}
Representações:
𝐴 = {1, 2, 3} , 𝐵 = {𝑥, 𝑦, 𝑧} e seja 𝑅 = {(1, 𝑦), (1, 𝑧), (3, 𝑦)}
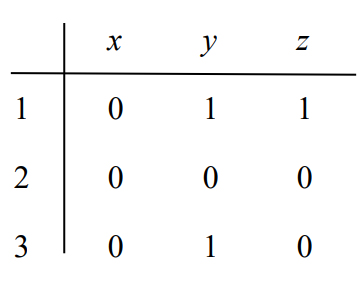

𝐴 = {1, 2, 3,4} e seja 𝑅 = {(1, 2), (2, 2), (2, 4), (3, 2), (3, 4), (4, 1), (4, 3)}

Função:
Toda função é uma relação
Transforma elementos de um conjunto origem em elementos de um conjunto saída
“CADA ELEMENTO DE UM CONJUNTO DE ENTRADAS DEVE ESTAR RELACIONADO A UM ÚNICO ELEMENTO DO CONJUNTO DE SAÍDAS”
Se não seguir a regra acima a relação não é função
Tipos:
Injetora:
Não há elemento em B com mais de um componente em A

Sobrejetora:
Qualquer elemento de B é imagem de, pelo menos, um elemento de A

Bijetora:
Se ela for injetora e sobrejetora

Função inversa:
A inversa de uma função f pode ser denotada por f-1

Para encontrar a inversa, deve-se trocar x por y
Exemplos:
f(x) = x + 5
y = x + 5
x = y + 5
x - 5 = y
f(x) = 2x – 3
y = 2x - 3
x = 2y - 3
x + 3 = 2y
x/2 + 3/2 = y
Função composta:
Genericamente, escrevemos h(x) = g(f(x)) ou (g ○ f)(x)
Exemplo:
f(x) = 2x + 2
g(x) = 5x
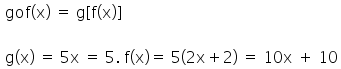
Função valor inteiro:
INT(x) converte x em um inteiro apagando a parte fracionária
Exemplos:
INT (42,98) = 42
INT (-42,98) = -42
INT (42) = 42
INT (-42) = -42
Função valor absoluto:
É o maior dos valores entre x e –x
ABS(x) ou |x|
Exemplos:
|-72,53| = 72,53
|72,53| = 72,53
Função floor:
Definição:
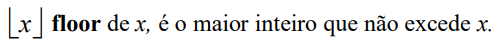
Exemplos:
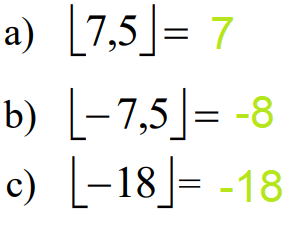
Função ceiling:
Definição:
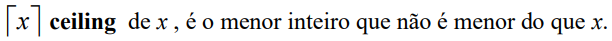
Exemplos:
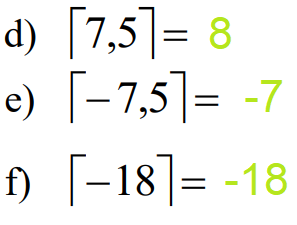
Função resto:
Seja k inteiro qualquer e M positivo, então k(modM)
Se k é negativo divida k por M para obter o resto r:
k (modM)=M-r
Exemplos:

 Knowt
Knowt