Ch.10- Circles

Vocab

Minor Arc

Less than half of the outline of the circle

0<X<180, named w/ 2 letters

The symbol is an arc over a segment

Major Arc

More than half of the outline of a circle

180<X<360, named with 3 letters

Arc over the 3-segment letters is the notation used to represent a major arc, indicating the longer path between the two endpoints on the circle.

Circumference

The total distance around a circle is represented in units. The formula is pi (d/diameter) or piR2, where R represents the circle's radius. This formula allows us to calculate the area enclosed within the circle.

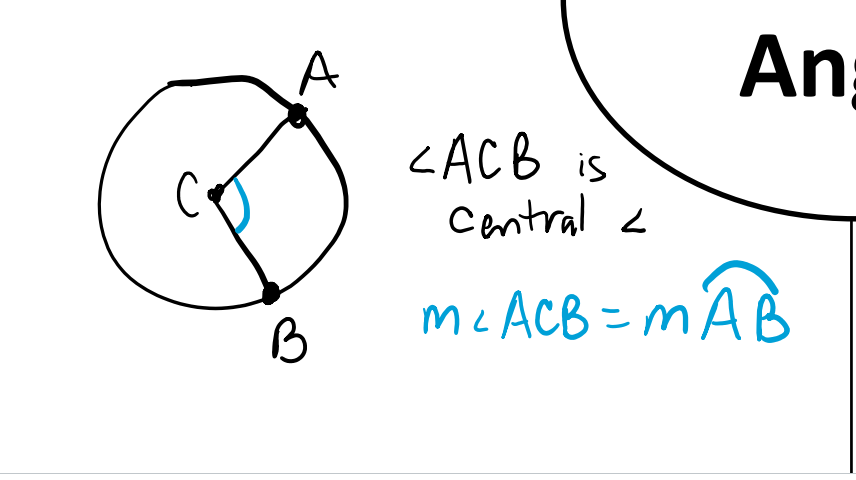
Central Angle

An angle in a circle where the vertex is the center of the circle.

The measure of the central angle is the same as its intercepted arc

Intercepted Arc

Part of a circle that’s created by an angle in a circle, ie, major/minor arc

Arc Length

The length of an arc in a circle

Fraction of the circumference, label is units- think 2πr( circumference)

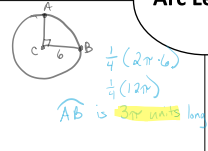
Arc Measure

The measure of an arc in a circle, labeled in degrees. -equal to the central angle

Radian

The measure of a central angle whose intercepted arc’s length is equal to the radius’s length

Label: rad

1 rad=~ 57.3 degrees

2πrad= 360 degrees

\ Circumference

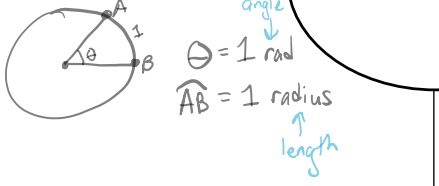
Sector

A wedge of a circle whose vertex is the center of a circle

Must contain part of the circumference and center of the circle

fraction of the circle- central</ 360 times 2πr

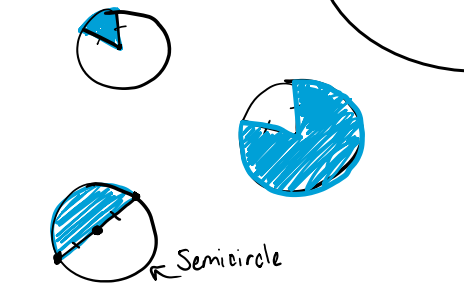
Chord

Segment inside of a circle whose endpoints are on the circumference

The diameter is a chord and also the longest one

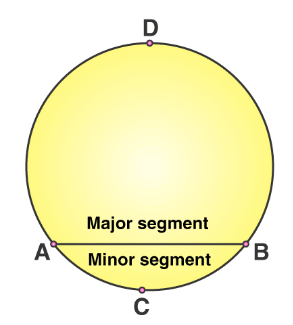
Segment of a Circle

Part of the area of the circle is created by the chord and its intercepted arc.

Label: Units

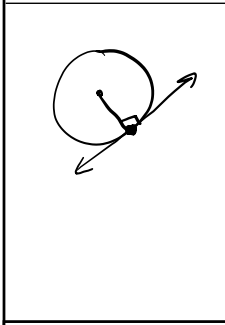
Tangent to a Circle

A line outside of a circle that only touches the circle in a single spot

Perpendicular to the radius @point of intersection

Inscribed angle

The angle in a circle whose vertex is ON the circle( circumference)

The measure of the inscribed angle is ½ the measure of its intercepted arc

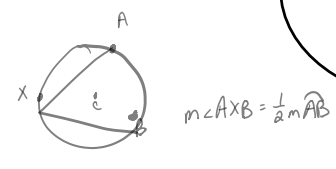
The Secant of a circle

A line outside the circle that intersects in 2 spots, a chord of a circle is a part of the secant.

Lesson 10-1

Arcs

Measure versus length

The measure of arc ABC is 240 degrees

The length of arc ABC is a fraction of the circumference

240*/360* times total circumference ~pi(20)= 41.9 Meters

Area-Sectors

Area of 30* Sector

Fraction of the total area of the circle

30/360 times pi10² = 1/12× 100pi/12= 25pi/3 cm2

focus on finding GCF and simplifying.

Area- Segments of Circles

Sector area- triangle area

98/360 times pi(3)² = 2.45pi

- 1/2(3)(3)sin(98*)~ 4.456

2.45pi- 4.456~ 3.2m²

Lesson 10-2

Tangents are equal to each other,

Lesson 10-3

If you connect the center of the circle to the end of the chord, you make the radius and an isosceles triangle

Lesson 10-4

Inscribed angles are exactly half of their intercepted arc; the arc measure is double of the inscribed angle. Central=Intercepted Arc, Central= 2x(Inscribed)

Diameter endpoints, inscribed angle is 90* because it is half of the intercepted arc.

Lesson 10-5

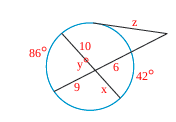
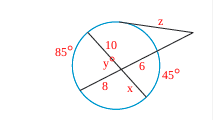
If the secants intersect inside the circle, the created angle is half the sum of the two intercepted arcs.

If the secants intersect outside of the circle, the angle is half of the difference of the angles.

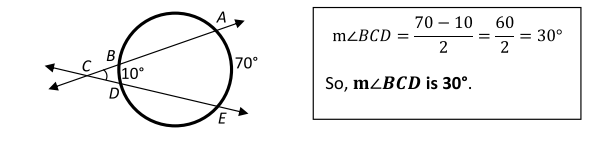
If you have a circle with intersecting secants, the inside angle is half of the average of the intercepted arcs, for this one, you would need to find BPC so that way BPC=1/2(X+124)

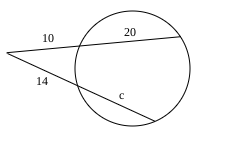
If you have a circle and you’re trying to find lengths of the secants, A(B)=C(d)

If you have two secant lines that intersect outside of the circle and you’re trying to find the length of one of them, you use the formula: A(A+B)= C(C+D)

Formulas

• Circumference: C = πd or C = 2πR

• Area: A = πR²

• Arc Length: L = (θ/360); fraction of total degrees * C

• Sector Area: A = (θ/360) * πR²

• graphing a circle (x-h)² +(y-k)²=r²

• formula for arc length: s = r𝜃. where s is the arc length, r is the radius, and 𝜃 is the central angle in radians. remeber to get rad, ⎍/180

• t'l;dr when trying to find the radius after you have 𝜃 is dividing it by itself → multiply by reciprocal

• When you have a inscribed angle and a further tangent created angle, the tangent is half of the inscribed

  

• m<1=1/2(A+B)- inside angle is the average of the two outer angles

/