P2 - Forces
P2.1 - Motion
P2.1.1 - Distance, time and speed
How do you measure distance and time in the laboratory?
Moving object | How to measure the distance | How to measure the time |
|---|---|---|
Trolley moving down a ramp | use a ruler/metre stick/tape measure | Use a stopwatch of light gates |
Falling object | use a ruler/metre stick/tape measure | use light gates |
Using a ruler, it is very difficult to measure large or small distances accurately. Using ultrasound is more accurate as the device measures the time taken for a pulse to travel there and back. This is used alongside the speed to work out the distance.
When using a stopwatch, there is a reaction time that will affect the results, as the stopwatch will either be paused before or after the object has completed. Light gates are much more accurate as a timer automatically starts and stops when an object interrupts the beam of light.
How do you calculate using the equation for speed?
In uniform motion the speed does not change, so this equation will be applicable:
speed (m/s) = distance (m) / time (s) OR distance (m) = speed (m/s) x time (s)
Non-uniform motion is where the speed is not constant. An example of this would be running a 100m race, and your average speed is 10m/s. Average speed means you were not always going at 10m/s; the speed fluctuated. To work out the average speed, use this equation:
average speed (m/s) = total distance (m) / total time (s)
How do you convert between units?
The standard unit of distance is metres, and the standard unit of time is seconds, but miles per hour is normally used when talking about fast moving objects like cars or cheetahs. However, it is often easier to convert all units to standard units when completing calculations. The standard unit of measure are the SI units.

P2.1.2 - Vectors and scalars
What is the difference between a vector and a scalar?
Some quantities, such as force, have both a magnitude and a direction. These are called vector quantities, and are shown using an arrow, with the size showing magnitude and the direction showing direction. Other quantities, like time (e.g. 30s) , have only magnitude. This means they are scalar quantities, as they have no direction.
What is the difference between displacement and distance?
Two common vector and scalars that often get confused are displacement and distance. Distance is how far you have travelled, for example 5km, but displacement is how far from the starting point you have travelled. This means that if you, for example, take a trip to someone else’s house, but you return home afterwards, your displacement will be 0km, even if your distance travelled is 100km.
Displacement is a vector quantity, and therefore, the direction needs to be stated, for example 10m east. Distance is a scalar quantity, so just 3km is fine.
What is the difference between speed and velocity?
Speed is a scalar quantity, so it only has magnitude (3m/s), but velocity is a vector quantity, so it has both magnitude and direction. This means they both need to be specified when writing the velocity, for example 5mph north.
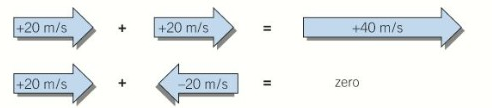
How do you add vector quantities?
P2.1.3 - Acceleration
What is acceleration?
The acceleration is the time it takes for an object to increase its speed by a certain amount, for example, from 0mph to 60mph. In other words, this is the change in velocity per second, and is measured in metres per second squared. If an object has a uniform acceleration, it means the acceleration does not change.
How can you calculate acceleration if you know the change in velocity?

Do you use speed or velocity to calculate acceleration?
To calculate acceleration, the change in speed is used. Therefore, it does not really matter which one is used, as the outcome answer should still be the same. It is better to refer to ‘slowing down’ as ‘negative acceleration’ than ‘deceleration’.
How do you calculate acceleration if you know the final and initial velocity?

P2.1.4 - Distance-time graphs
What does a graph of distance against time mean?
A graph of distance against time tells you about the speed of an object on its journey. The speed is equal to the gradient of the graph. Here is an explanation for what the different gradients mean.
A straight line means the object’s speed is constant, as the gradient of the line does not change.
A horizontal line means that the object is stationary, as it is travelling no distance, but time is still increasing.
The steeper the line, the faster the object is travelling, as more distance is being covered in a shorter amount of time.
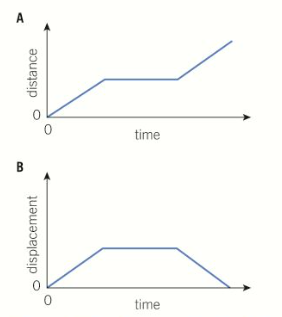
How is a distance-time graph different to a displacement-time graph?
A distance-time graph (A) shows the total distance travelled by an object. In a displacement-time graph (B), the gradient can be either positive (away from starting point), negative (towards starting point) or zero. The gradient of the graph is its velocity, so it has direction as well as magnitude.
P2.1.5 - Velocity-time graphs
What can you deduce from the gradient of a graph?
Any graph with time on the x-axis tells you about rate of change with time. The rate of change of speed or velocity with time is also known as acceleration. This table shows which graphs you can plot knowing what measurements.
Measure | Plot | Gradient equals | Then plot | Gradient equals |
|---|---|---|---|---|
Distance travelled and time | Distance-time graph | Speed | Speed-time graph | Acceleration in magnitude only |
Distance from a starting point and time | Displacement-time graph | Velocity | Velocity-time graph | Acceleration in magnitude and direction |
How do you calculate distance travelled?
The distance is the area under a velocity-time graph. The area can be split up with any shapes to make it easier to work out the area, just remember to add them together at the end. This works because speed multiplies with time to get distance.
P2.1.6 - Equations of motion and kinetic energy
What is an equation of motion and how do you use it?
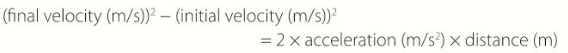
Displacement may also be referred to in the equation instead of distance as they have the same value.

How do you calculate kinetic energy?
Energy can be transferred to and from different stores. One of those stores is kinetic energy. The energy transferred from an energy store can be calculated by the following equation (in joules).
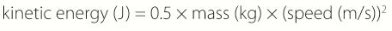


P2.2 - Newton’s laws
P2.2.1 - Forces and interactions
How do forces arise?
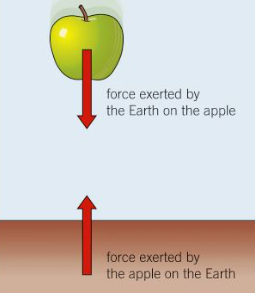
Pairs of forces arise when they interact. This is called an interaction pair. Listed below are the rules an interaction pair must follow:
Each force acts on a different object.
The forces are the same size, for example 267N.
The forces are the same type, for example gravitational.
The forces act in opposite directions.
This is also known as Newton’s Third Law. It is essentially ‘every action has an equal and opposite reaction’ or ‘forces always come in pairs’.
What are non-contact forces?
A non-contact force is when an object can interact with another object without touching it. These are some examples of non-contact forces you may have already come across:
gravity
electrostatics
magnetism
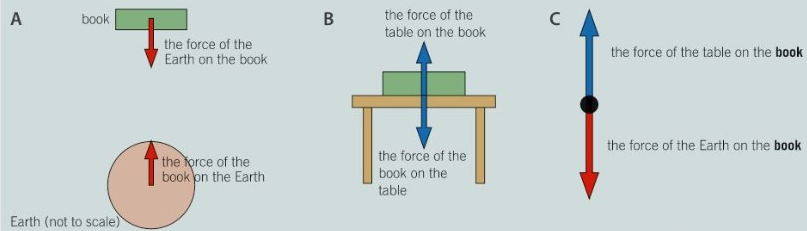
These forces arise because they can interact with another object at a distance, so long as that object is in the field of the force. The field is the area that an electrical charge, a magnetic material or a mass experiences a force. The force arrow of a non-contact force is drawn from the centre of an object’s mass.
On a diving board, the gravitational force of the earth pulls you towards the centre of the earth. However, you also pull the earth, just by such a small amount as the mass of the earth is so large that it is immeasurable.
What are contact forces?
A contact force is the opposite of a non-contact force. A contact force is exerted when two objects touch each other. For example, if you were standing on a diving board, the board pushes up on you, but you also push down on the board. The force arrows drawn for a contact force are drawn from the point of contact. Here is a table with some examples of contact forces:
Contact force | Interaction pair | How it is produced |
|---|---|---|
Friction on a sliding box | The force of the box on the surface.The force of the surface on the box. | The atoms that make up the surfaces interact when rough surfaces slide over each other. |
Drag on a falling leaf | The force of the falling leaf on the air.The force of the air on the falling leaf. | The particles in the gas collide with the object and the object pushes them away. |
Normal contact force acting on an elephant | The force of the elephant on the ground.The force of the ground on the elephant. | Solid objects deform slightly when you exert a force on them. The bonds within the object are compressed. |
Upthrust on a floating boat | The force of the boat on the water.The force of the water on the boat. | Gravity produces pressure differences in a fluid. The pressure produces a net upwards force. |
Tension in the cord of a bungee jumper | The force of the bungee jumper on the bungee cord.The force of the bungee cord on the bungee jumper. | Solid objects deform slightly when you exert a force on them. The bonds between the particles are stretched. |
Remember that weight is just the gravitational force of one object on another. As a force is a vector, we can represent them with an arrow. The size of the arrow is equal to the magnitude, and the direction of the arrow is equal to the direction of the force.
P2.2.2 - Free body diagrams
What is a free body diagram?
A free body diagram is a diagram showing the forces acting on a single object as it performs a certain action. The object is normally depicted as a box, and the forces acting on the object are shown by force arrows. The free body diagram can be useful to work out which forces are acting where, or explain the motion of an object, or to do a calculation.
How do you draw a free body diagram?
The force (or forces) acting on an object can be from several different interaction pairs.
Identify all the non-contact force pairs.
Identify all the contact force pairs.
Focus on a single object. Draw that object (as a box) with arrows that represent all the different forces acting on that object.
How do you find the resultant force?
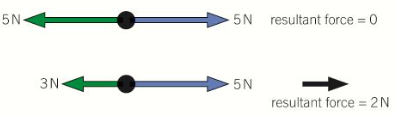
The resultant force or net force can be found using the free body diagram. However, as force is a vector, you need to ensure to take the direction the forces act into account when adding/subtracting them.
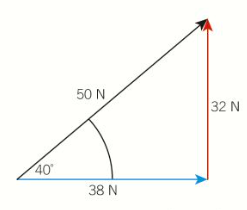
Sometimes forces act at different angles to each other. Pythagoras’ theorem can be used to calculate forces that are perpendicular to each other.

How do you resolve forces?
You can work out the resolution of the forces (which two forces at right angles made the resultant force), by drawing a triangle on some graph paper and measuring it with a ruler. Ensure there is a scale and use a protractor for the angle so that the results are accurate.
P2.2.3 - Newton’s First Law
What is Newton’s First Law?
When you are standing on a bus or train, it sometimes feels as though you are going to fall over or that you are being flung about. This is all down to Newton’s First Law.
What is actually happening is that as the bus's velocity changes, yours stays constant. So while the bus turns, you continue travelling in a straight line. This results in you jolting to the side to regain balance.
Newton’s First Law states that any object will continue to stay at rest or move with uniform velocity unless a force acts on it.
It takes a resultant force to change the motion (speed and direction) of an object. That means that if the resultant force is zero, then the speed or direction of an object will not change. Therefore, this law is really about inertia. Inertia is the measure of how difficult it is for an object to change its velocity. If an object is stationary, it stays stationary, whereas if an object is moving it will stay moving.
Why do objects continue to move at a steady speed?
Friction is a force that acts on almost all moving things and tends to stop things moving.
If the speed or direction does not change, then the resultant force is zero. A steady speed means that there is zero resultant force.
What is equilibrium?
When the resultant force is zero, the speed does not change. This means the object is in equilibrium.
P2.2.4 - Newton’s Second Law
What happens when the resultant force is not zero?
A leaping animal uses its back legs to exert a force on itself. Its motion changes because there is a resultant force. A resultant force can
change the speed of an object.
change the direction of an object.
change both the speed and direction of an object.
If the speed or direction change, then an object accelerates.
Why are there resultant forces on some objects?
Free body diagrams can be used to illustrate objects upon which a resultant force is acting.
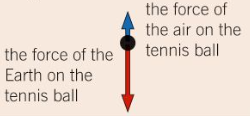
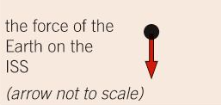
A tennis ball accelerates towards the ground. | The ISS orbits the Earth. |
|---|---|
|
|
Result: The ball will accelerate towards the ground. | Result: The ISS move in a circle, at a steady speed. |
How do you calculate with Newton’s Second Law?
Newton’s Second Law states that the resultant force produces and acceleration on the object that depends upon:
 Knowt
Knowt