Math - 10e année

Système linéaire ou système d’équations

Déf: Un système linéaire ou système d’équations du degré, est un ensemble d’au moins deux équations qu’on résoudre simultanément

On note: y = a₁ x +b₁     y = a₂ + b₂ ou     a₁x + b₁y = c₁    a₂x + b₂y = c₂

Résoudre un système linéaire consiste à déterminer les coordonnées du ou des points d’intersection entre les deux droites. Si ce point existe, il sera noté (x₁y).

Méthodes de résolution d’un système linéaire

Méthode graphique

Cette méthode consiste à tracer les deux droite dans le plan cartésien et de vérifier leurs positions.Le système d’équations formé par ces deux équations qui ont donné le point d’intersection a une seule solution qui est I(x_iy_i)

1. Strictement parallèles
   Les deux droites sont strictement parallèles. On note: D₁ // D₂
   Alors, le système d’équations de les deux droites n’a pas de solution.

2. Parallèles confondues
   Ces droits sont parallèles confondues alors ce système d’équations a une infinit; de solutions.

Résolution de système linéaire par substitution

Résoudre par substitution signifie:

1. Isoler une variable dans une équations.

2. Remplacer cette l’expression de cette variable dans l’autre équation.

EX: Résous par substitution le système 1) 4x + 3y = 1       2) 3x + y = 7
Dans l’équation 2) isolons y     y = 7 - 3x

Méthode d’élimination

1. Méthode d’addition
   EX: Résous le système
   3x + 2y = 19
   5x - 2y = 5
   

Résolution des problèmes à l’aide d’un système d’équations

Pour résoudre un problème à l’aide d’un système d’équations, il faut respecter les étapes suivantes:

1. Choix des inconnues
   Identifier les inconnues et nommez-les à l’aide des variables x et y après lecture du problème.

2. Mise en équations
   Traduire les informations de l’énoncé en équation

3. Résolution du système
   Résoudre le système par la méthode de votre choix

4. Retour au problème
   Répondre à la question du problème

Géométrie Analytique

Segment de droite

Déf: Un segment de droite est une partie de droite bonnée (limitée) dans le sens.
On note: [A,B] avec A (x_a, y_a) et B(x_b, y_b)

Le point milieu d’un segment

Déf: c’est le point qui divise le segment en deux segments congrus.

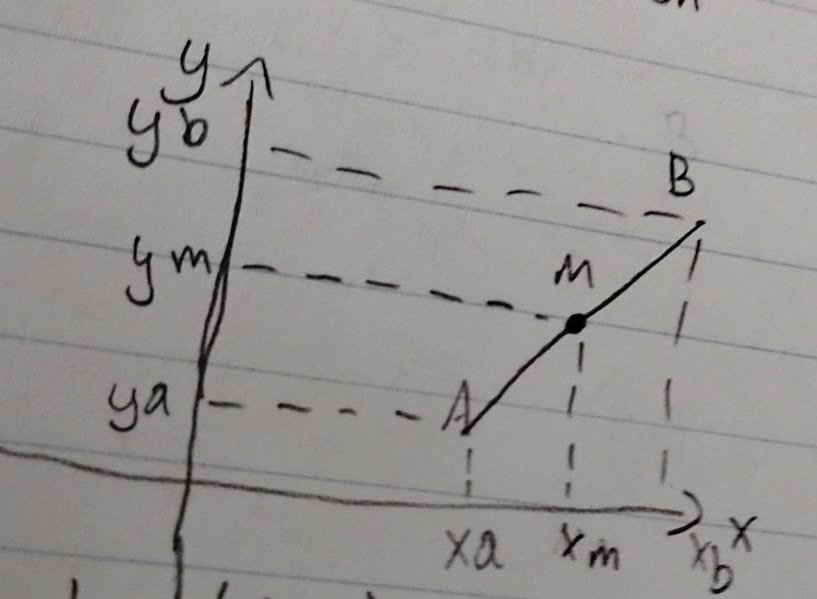
On note: M (x_m, y_m)

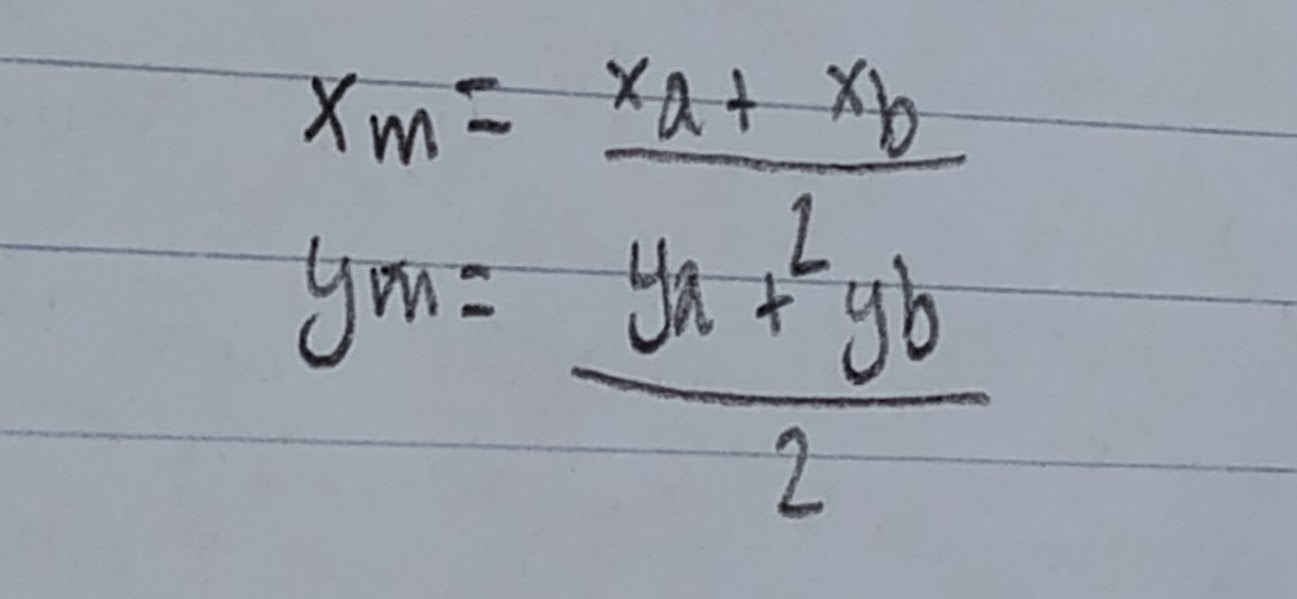
- La médiane d’un triangle

Déf: La médiane d’un triangle est un segment de droite qui relie un sommet au milieu du côté opposé.

Équation de la médiane

Soit le triangle ABC dans le plan cartésien avec A (-3, 3); B (2, -5) et C(5, 2).

Soit le triangle ABC dans le plan cartésien avec A (-3, 3); B (2, -5) et C(5, 2). - La médiane issue ou sommet C

Le sommet C a pour côté opposé AB soit M le milieu de AB.

Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - Le sommet C a pour côté opposé AB soit M le milieu de AB. - La médiatrice d’un segment

Déf: Une médiatrice est une droite perpendiculaire à un de droite et que le divise en deux parties égales.

Pour la pente de la perpendiculaire, on doit renverser la fraction et changer le signe.

La longueur d’un segment de droite

Déf: La longueur d’un segment de droite, c’est la distance entre ces deux bornes.

Ce qui montre que le côté AB opposé à C est l’hypoténuse.

Théorème de Pythagore

L’hypoténuse au carré égale à la somme des carrés de deux autres côtés

AB² = AC² + BC²

NOTE BIEN

La distance ou la longueur doit être positive.

NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - NOTE BIEN - La distance la plus courte entre une droite et un point

Détermine la d

Étapes

1. Pente de la droite est 1

2. Pente de la perpendiculaire à cette droite
   m = -1

3. Équation de la droite de pente m = -1 et passant par la point A(2, 3)
   

4. Point d’intersection de ces deux droites: Il faut résoudre le système

5. Distance entre les points A(2, 3) et S(0, 5)

Équation du cercle de Rayon (R) centré à l’origine

r² = x² + y²

Les relations du second degré

Les relations non-linéaires

Déf: Une relation non-linéaire est une relation entre deux variables, dont la représentation graphique n’est pas une droite.

Dans une relation non-linéaire:

• la variable indépendante est celle qu’on peut contrôler avant le début de l’expérience

• la variable dépendante est celle qu’on peut mesurer pendant l’expérience et elle varie quand la variable indépendante

On peut aussi dire qu’une relation est non-linéaire si la relation entre x et y n’est pas de la forme y = ax + b avec a et b des nombres réels n’égale pas à 0.

Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant

Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Dans la relation non-linéaire, le taux de proportionnalité n’est pas constant - Les relations du second degré

Déf: une relation du second degré est une relation oi l’équation est de la forme y = ax² + bx + c ou a, b et c sont des nombres réels et a n’égale pas à 0. Sa représentation graphique s’appelle LA PARABOLE qui a la forme de U.

Les caractéristiques principales de la parabole

• Forme de la courbe
  Elle est ouverte vers le haut (comme un U) si a > 0, ou soit ouverte vers le bas (comme un n) si a < 0. (On dit aussi SENS DE LA CONCAVITÉ)

• Axe de symétrie
  C’est une droite verticale d’équation x = -(b/2a)
  Il sépare la parabole en deux parties congruentes qui sont l’image par réflexion l’une de l’autre

• Sommet
  C’est le point ou la parabole change de direction.
  S(-b/2a, f(-b/2a))
  Si a > 0 alors le sommet est un MINIMUM
  Si a < 0 alors le sommet est un MAXIMUM

Donc le sommet est l’intersection de l’axe de symétrie et la parabole

Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Donc le sommet est l’intersection de l’axe de symétrie et la parabole - Différences finies pour déterminer la nature d’une relation

Déf: Les différemces finies, sont les différences entre les valeurs de y dans une table de valeurs ou l’écart de valeurs de x est constant.

Les premières différences

Ils sont les différences entre les valeurs consécutives de y. Si ces différences sont les mêmes alors la relation définie par la table de valeurs est une relation linéaire de la forme y = ax + b ou y = ax

Les deuxième différences

Ils sont les différence entre les premières différences consécutives et si elles sont toutes égales alors la relation est du second degré.

Les Transformation du second degré

Une fonction du second degré est définie par l’équation y = ax² + bx + c ou a, b et c dont des nombres réels et a est différent que 0

Sa représentation graphique dans le plan cartésien est une parabole.

Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - Sa représentation graphique dans le plan cartésien est une parabole. - La fonction du second degré transformé

1. La forme centrée à l’origine
   f(x) = ax² ou y = ax²
   Si a = 1 →f(x) = x2 (fonction de référence)

2. La forme générale
   f(x) = ax² + bx + c

3. La forme canonique
   y = a(x-h)² + k

4. La forme factorisée
   f(x) = a(x - x₁)(x - x₂)

Ces transformations permettent d’analyser la fonction, de trouver son sommet S(h, k) ou ses racines (x₁ , x₂) et de modifier le graphique de la parabole de la fonction la référence y = x².

Fonctions du second degré = fonctions quadratiques

Pour la fonc tion de référence y = ax2 (f(x) = ax2)

Le coefficient a dans l’équation y = ax2 détermine si la parabole est un agrandissement (étirement) vertical ou rétrécissement (compression) vertical.

Effet du coefficient a

Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Effet du coefficient a - Agrandissement (étirement) vertical

La parabole devient plus étroite. Cela se produit lorsque la valeur absolue de a est plus grande que 1. Si lal > 1

EX: Dans la fonction y = 2x², la parabole sera plus étroite que celle de y = x²

Rétrécissement (compression) vertical

La parabole devient plus large. Cela se produit lorsque la valeur absolue de a est entre 0 et 1. 0 < lal < 1

EX: Dans la fonction y = 0.5x² la parabole sera plus large que y = x²

Effet du signe de a

Le signe du coefficient a détermine l’orientation ou l’ouverture de la parabole et, non son agrandissement ou rétrécissement.

Si a > 0, la parabole tourne vers le haut.

Si a < 0, la parabole tourne vers le bas.

De plus, la valeur absolue de a affecté la largeur de la parabole : plus |a| est grand, plus la parabole est étroite, tandis que plus |a| est petit, plus la parabole est large.

Fonction de référence y = x² a = 1

La référence du graphique de la fonction par rapport à l’axe des x

• Lorsque a est positif (a > 0)
  L’ouverture de la parabole est vers le haut

• Lorsque a est négatif (a < 0)
  L’ouverture de la parabole est vers le bas

On dit que la parabole de y = x² a subit une réflexion par à l’axe des x

L’effet des modifications d’un paramètre sous la forme canonique

Formule: la forme canonique est y = a(x - h)² + k (ou a, h et k sont des paramètres de la fonction avec a n’égale pas à 0)

L’analyse de la paramètre h

Lorsque h est positif (h > 0), la courbe subit une translation horizontale vers la droite.

Lorsque h est négatif (h < 0) la courbe subit une translation horizontale vers la gauche.

Analyse de paramètre k

Lorsque k est positif, la courbe subit une translation vers le haut.

Lorsque k est négatif, la courbe subit une translation vers le bas.

Dans la forme canonique , les paramètres h et k fournissent des coordonnées du sommet de la parabole dans le plan cartésien S(h, k)

y = a(x - h)2 + k →sommet S(h, k)

axe de symétrie a pour équation x = h

Extremum y = k

nature → Maximum si a < 0

Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k - Extremum y = k -      → Minimum si a > 1

Les relations du second degré de la forme y = a(x - r)(x - s)

Déf: Une relation de la forme y = a(x - r)(x - s) est une relation du second du second degré. Les abscisses à l’origine ou zéros, sont r et s. Cette est dite forme factorisée.

Représentation graphique

r et s étant abscisses à l’origine, ou les note: (r, 0) et (s,0).

Le milieu des abscisses à l’origine (r + s)/2 est l’équation de symétrie de l’axe de symétrie et l’abscisse du sommet.

S(r+s/2, y) = S(r+s/2, f(r+s/2))

Il faut déterminer la valeur de a si elle n’est pas donnée.

S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - S(r+s/2, y) = S(r+s/2, f(r+s/2)) - Les polynômes

Monôme:

Déf: Un monôme est une expression algébrique qui contient qu’un seul terme, former par la multiplication d’une partie numérique (coefficient) et d’une partie littérale (une ou plusieurs variables avec des exposants entiers naturels)

Degré de monôme

Déf: Le degré d’un monôme correspond à la somme des exposants de toutes ses variables.

Toute constante est de degré 0

EX: 3x a degré 1

Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Toute constante est de degré 0 - Polynôme

Déf: Un polynôme est une expression algébrique qui est la somme de monômes et chaque monôme est appelé TERME

Degré de polynôme

Déf: Le degré d’un polynôme correspond au degré le plus élevé de ses termes.

Classification de polynômes

Les polynômes se classent selon leur nombre de termes ou leur degré

Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification de polynômes - Classification par nombre des termes

- Classification par degré

- Les termes d’un polynôme

On écrit généralement les termes d’un polynôme de manière que les exposants de la variable soient en ordre décroissant ou croissant.

EX: Ordre décroissant: 2x³ - 3x² + 5x + 9 (degrés sont en décroissance)

Ordre croissant: 9 + 5x - 3x² + 2x² (degrés sont en croissance)

Termes semblables

On dit que deux termes sont semblables lorsqu’ils ont la ou les même(s) variables et mêmes exposant.

EX: -3x et 5x →(sont semblables)

-3x et 5x² →(ne sont pas semblables, différents exposants)

-3x et 5y →(ne sont pas semblables, différentes variables)

2x²y et 7x²y →(semblables)

2x²y et 7xy² →(ne sont pas semblables)

Simplification d’une expression (d’un polynôme)

Pour simplifier un polynôme, il faut:

1. Repérer les termes semblables et les regrouper

2. Additionner les coefficiente
   C’est ce qu’on appelle REGROUPEMENT DES TERMES SEMBLABLES

EX: Addition des polynômes

Simplifie (x² + 4x - 2) + (2x² - 6x + 9)

x² + 4x - 2 + 2x²- 6x + 9

x² + 2x² + 4x - 6x - 2 + 9

3x² - 2x + 7

EX: Soustraction des polynômes

Simplifie (6m² - mn + 4) - (7m² + 4mn - 2)

6m² - mn + 4 - 7m² - 4mn + 2

6m² - 7m² - mn - 4mn + 4 + 2

-m² - 5mn + 6

EX: Multiplication des monômes

(2x²)(7x) = 14x³

(-4a²b)(3ab³) = -12a³b⁴

Le développement et la simplification des expressions

Développe et simplifie

3x(x - 2) - 2x(2x + 5)

3x² - 6x - 4x² - 10x

3x² - 4x² - 6x - 10x

-x² - 16x

Produits remarquables ou produits spéciaux

1. (a + b)(a + b) = a(a + b) + b(a + b)
   (a + b)(a + b) = a² + ab + ba + b²
   (a + b)(a + b) = a² + 2ab + b²
   (a + b)² = a² + 2ab + b²

2. (a - b)(a - b) = a(a - b) - b(a - b)

   (a - b)(a - b) = a² - ab - ba + b²

   (a - b)(a - b) = a² - 2ab + b²

   (a - b)² = a² - 2ab + b²

3. (a + b)(a - b) = a(a - b) + b(a - b)
   (a + b)(a - b) = a² - ab + ba - b²
   (a + b)(a - b) = a² - b²

Facteur Commun

Déf: Un facteur commun est un nombre ou une expression qui divise plusieurs nombres ou expressions sans laisser reste

EX: les nombres 12 et 18

Facteurs de 12: 1, 2, 3, 4, 6, 12

Facteurs de 18: 1, 2, 3, 6, 9, 18

Facteurs communs: 1, 2, 3, 6

PGFC = 6

Expression: 2x² - 7x

• 2x² peut s’écrire comme 2 × x × x

• 7x peut s’écrire comme 7 × x

Le facteur commun est x

Un polynôme est factorisé ou décomposé en facteur lorsqu’il se présente sous forme d’un produit de polynôme.

Il est impossible de factoriser davantage un polynôme lorsqu’il n'y a pas plus un facteur commun variable ou entier autre que 1 ou -1.

EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé.

EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - EX: 2x + 5 Facteur est 1. Alors 2x + 5 ne peut pas être factorisé. - Un facteur commun monômial

Factorise 8x³ - 6x²y² + 4ײy

8x³ = 2 × 2 × 2 × x × x × x

6x²y² = 2 × 3 × x × x × y × y

x²y² = 2 × 2 × x × x × y × y

PGFC = 2x²

8x³ - 6x²y² + 4ײy = 2x²(4x - 3y² + 2y)

(Forme développé) (Forme factorisé)

(Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - (Forme développé) (Forme factorisé) - Un facteur commun binômial

Factorise 4x(w + 1) + 5y(w + 1)

(w + 1)(4x + 5y)

Certains polynôme ne possèdent aucun facteur commun à tous leurs termes. On peut cependant les factoriser en groupant ces termes qui ont un facteur commun

La factorisation par groupement

Factorise: ac + bc + ad + bd

Il n’y a pas un facteur commun à tous ces termes on doit alors procéder par groupement des termes qui ont un facteur commun.

Groupement:

(ac + bc) + (ad + bd)

c(a + b) + d(a + b)

(ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - (ac + bc) + (ad + bd) - Factorisation du trinôme du second degré: y = ax² + bx + c

si a = 1 y = ax² + bx + c

pour factoriser un tel trinôme, on doit trouver deux nombres m et n tels que

m + n = b (somme)

mn = c (produit)

alors y = x² + bx + c = (x + m)(x + n)

mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - mn = c (produit) - si a n’égale pas 1

Produit = ac

Somme = b

Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Produit = ac - Factorisation des produits spéciaux

(a + b)² = a² 2ab + b²

(a - b)² = a² - 2ab + b²

Carré d’un binôme et trinôme carré parfait

(a équation