Key Concept of Electrostatic Potential Energy Know for AP Physics C: E&M
Introduction
Electrostatic Potential Energy (EPE) refers to the energy stored in a system due to the relative positions of charged particles. It arises from the electric forces between charged objects and is a key concept in understanding how charges interact in an electric field. In this reviewer, we will explore the fundamental principles of electrostatic potential energy, its relationship with work and force, and how it fits within the broader context of electrostatics.
1. Understanding Electrostatic Potential Energy
Electrostatic potential energy is the energy stored in a system of charges due to their positions relative to each other. It depends on the nature of the charges and their separation distance.
Formula for Electrostatic Potential Energy
The electrostatic potential energy (U) between two point charges q1 and q2 separated by a distance r is given by:
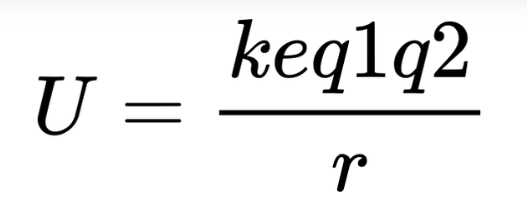
Where:
ke = Coulomb's constant (8.99×109N⋅m^2/C^2)
q2 = Magnitudes of the charges
r = Distance between the charges.
Important Notes:
Significance of the Formula: The formula expresses the interaction energy between two point charges based on their magnitudes and separation distance. The sign of U tells you whether the force is attractive (negative U) or repulsive (positive U).
Energy and Force Relationship: The electrostatic potential energy is related to the work done in bringing the charges from infinity to their current position. The force between charges derives from the gradient of this potential energy.
2. The Nature of Electrostatic Potential Energy
Repulsive and Attractive Interactions
If q1 and q2 have the same sign (both positive or both negative), the potential energy is positive, indicating a repulsive force.
If q1 and q2 have opposite signs, the potential energy is negative, indicating an attractive force.
Energy Considerations
When like charges move closer together, energy is stored in the system (increased potential energy), while opposite charges moving closer release energy as they attract.
3. Electrostatic Potential Energy in Systems of Multiple Charges
For a system with more than two charges, the total electrostatic potential energy is the sum of the potential energies between each pair of charges. This is a key concept when analyzing complex charge systems, such as charge distributions on conductors or the electric field of an array of charges.
Multiple Charges (Example)
For a system of charges q1, 2, and 3, the total potential energy is:
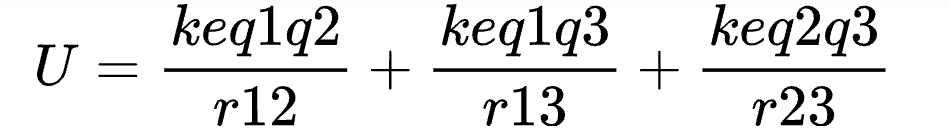
Where rij is the distance between charges i and j.
Key Insights
In systems with more than two charges, the total electrostatic potential energy will depend on both the magnitudes and distances between all pairs of charges. This makes electrostatics a critical part of understanding interactions in molecules and materials.
4. Work and Electrostatic Potential Energy
Work and electrostatic potential energy are intimately related. The work done by the electrostatic force in moving a charge depends on the change in potential energy.
Work Done in Moving a Charge
The work required to move a charge qqq in the electric field of another charge is equal to the change in potential energy ΔU of the system: W=−ΔU
Negative Work: If the system loses potential energy (e.g., attractive forces bring opposite charges together), the work done by the electric force is negative, as energy is released.
Positive Work: If the system gains potential energy (e.g., like charges are moved closer together), the work done is positive, as energy is stored.
5. Electric Potential vs. Electrostatic Potential Energy
Electric Potential (V)
Is defined as the potential energy per unit charge at a point in space:
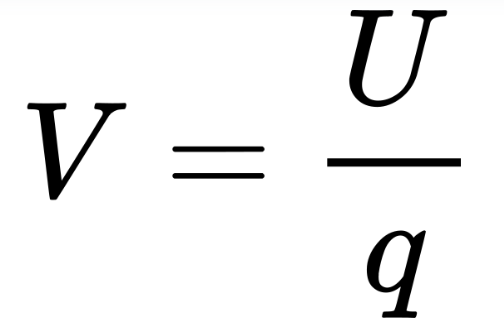
Where V is the electric potential, U is the electrostatic potential energy, and q is the charge experiencing the potential.
Relationship Between U and V
The electrostatic potential energy of a point charge qqq in an electric field is related to the electric potential V at the position of the charge by:
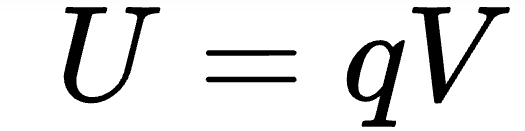
This means the electrostatic potential energy depends both on the charge and the electric potential at its position.
6. Equipotential Surfaces
Equipotential surfaces are surfaces where the electric potential is constant. No work is required to move a charge along an equipotential surface, as there is no change in electric potential.
Relationship with Electric Field
The electric field lines are always perpendicular to equipotential surfaces.
The direction of the electric field is always from regions of higher potential to lower potential.
Key Insight
Understanding equipotential surfaces is useful when analyzing electric fields and potential, as it allows you to visualize how a field influences charge movement.
7. Energy Conservation in Electrostatics
In electrostatic systems, energy conservation is a fundamental principle. The total mechanical energy (kinetic energy + electrostatic potential energy) of a system remains constant if only electrostatic forces are acting.
Energy Transfer
When charges move in an electric field, the electrostatic potential energy can be converted to kinetic energy (or vice versa). For example, if a charged particle moves in the direction of the electric field, it gains speed (kinetic energy) and loses potential energy.
Uniform Electric Field
In a uniform electric field, the potential energy of a charged particle is related to the displacement in the field:
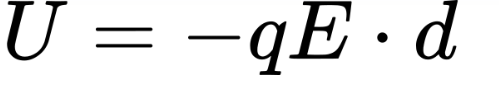
Where E is the electric field strength, d is the displacement of the particle, and q is the charge.
8. Additional Knowledge
Coulomb’s Law and Electrostatic Force
Coulomb’s Law describes the force between two charges:
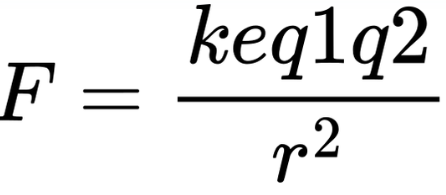
The electrostatic force is attractive if the charges have opposite signs, and repulsive if they have the same sign.
Connection to Potential Energy
The electrostatic potential energy can be derived from Coulomb’s law. The energy stored in the system due to the force between charges is essentially the "work" done to assemble the configuration of charges.
Energy Stored in a Capacitor
The electrostatic potential energy stored in a capacitor is another crucial application:
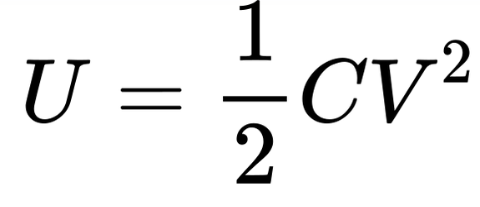
Where:
C is the capacitance of the capacitor,
V is the voltage across the capacitor.
Key Insights
This formula shows that the energy stored in a capacitor depends on the charge stored and the voltage across it. Capacitors are used extensively in circuits to store and release energy, and their behavior is rooted in electrostatic principles.