Randomisation Blinding Sample Size Calculations flashcards

Topic 3: Randomisation, Blinding and Sample Size Calculations

• Instructor: Lizzie Chappell

• Date: 4th March 2025

Fundamentals of Design for Major Randomized Controlled Trials

Choice of Patients and Centers

• Set precise eligibility criteria:

  • Not too specific nor too broad.

• Prefer large-scale, multicenter trials to ensure geographic representation.

Choice of Treatments

• Specify precise treatment regimens.

• Include placebo/sham control group or active comparator.

• Consider a 3-arm trial for comprehensive evaluation.

Choice of Outcomes

• Define the primary efficacy endpoint clearly.

• List secondary endpoints.

• Incorporate safety concerns into the overall outcome priorities.

Randomization

• Allocation concealment is crucial to avoid bias.

• Choose a statistical method for randomization.

• Stratification can help ensure balance in groups but may not be key in large trials.

• Consider unequal randomization favoring new treatment in certain situations.

Use of Blinding

• Aim for double-blind trials when feasible:

  • If not, blinded evaluation required.

  • Especially important for subjective endpoints.

Choice of Trial Size

• Use power calculations to determine required trial size.

• Choose a realistic anticipated effect size.

• Compromise may be needed for practical target size.

Objectives of Randomisation

• Eliminate bias in treatment group allocation.

• Ensure treatment groups do not differ systematically.

• Balance known and unknown prognostic factors.

• Aim is to allocate treatments independently of patient characteristics.

Types of Randomisation

Simple Randomisation

• Randomise patients using simple methods:

  • E.g., Coin toss or dice rolls.

• Advantages:

  • Quick, no special technology required.

• Disadvantages:

  • Potential for unbalanced groups, losing statistical power.

Random Permuted Blocks

• Construct a randomization list using blocks to ensure balance:

  • Example block sequences (length of 4): AABB, ABAB.

• Maintain small differences in group sizes.

Stratification

• Balances treatment groups concerning specific patient characteristics:

  • Common factors: center, disease stage, age, sex, disease markers.

• Create separate randomisation lists for each stratum.

Minimisation

• Addresses balancing multiple stratification factors:

  • Avoids predictability while maintaining random allocation.

  • Controversial due to potential predictability in allocation.

Sample Size Calculations

Importance of Sample Size

Sample Size Calculation

To perform a sample size calculation assuming you have significance level (α) and statistical power (1 - β), follow these steps:

1. Determine the Null and Alternative Hypotheses:

   • Null hypothesis (H0): e.g., Mean reduction in blood pressure is the same in both groups.

   • Alternative hypothesis (H1): e.g., Mean reductions differ.

2. Specify Key Factors:

   • Significance Level (α): Probability of Type I error (false positive).

   • Statistical Power (1 - β): Probability of correctly rejecting the null hypothesis when the alternative hypothesis is true.

   • Effect Size (Δ): The expected difference in treatment outcomes that you aim to detect.

   • Variability (σ²): The expected variability in your outcome measure.

3. Use the Appropriate Formula: For continuous outcomes, the function can be represented as:

   • f(α, β) = applied values of significance and power. This function helps to compute the total sample size needed. For binary outcomes, the formula becomes:

   • n_{group} = \frac{\pi_1(1 - \pi_1) + \pi_2(1 - \pi_2)}{(\pi_2 - \pi_1)^2} f(α, β) where (\pi_1) and (\pi_2) are the proportions in the two groups.

4. Calculate Required Sample Size:

   • Plug the values of α, β, Δ, and σ² into the formula to find the required sample size for each group. Adjust the sample size as needed based on the context of your trial.

5. Consider Practicalities:

   • Ensure that the calculated sample size is feasible ethically and logistically for your trial design.

• Excessive sample size is unethical and inefficient.

Hypothesis Testing

• Null hypothesis (H0): e.g., Mean reduction in blood pressure is the same in both groups.

• Alternative hypothesis (H1): e.g., Mean reductions differ.

Types of Error

• Type I error: False positive (reject H0 when true).

• Type II error: False negative (fail to reject H0 when it should be).

Statistical Terms

• Significance (Probability of type I error, α)

• Power (Probability of rejecting H0 given that H1 is true, 1 - β).

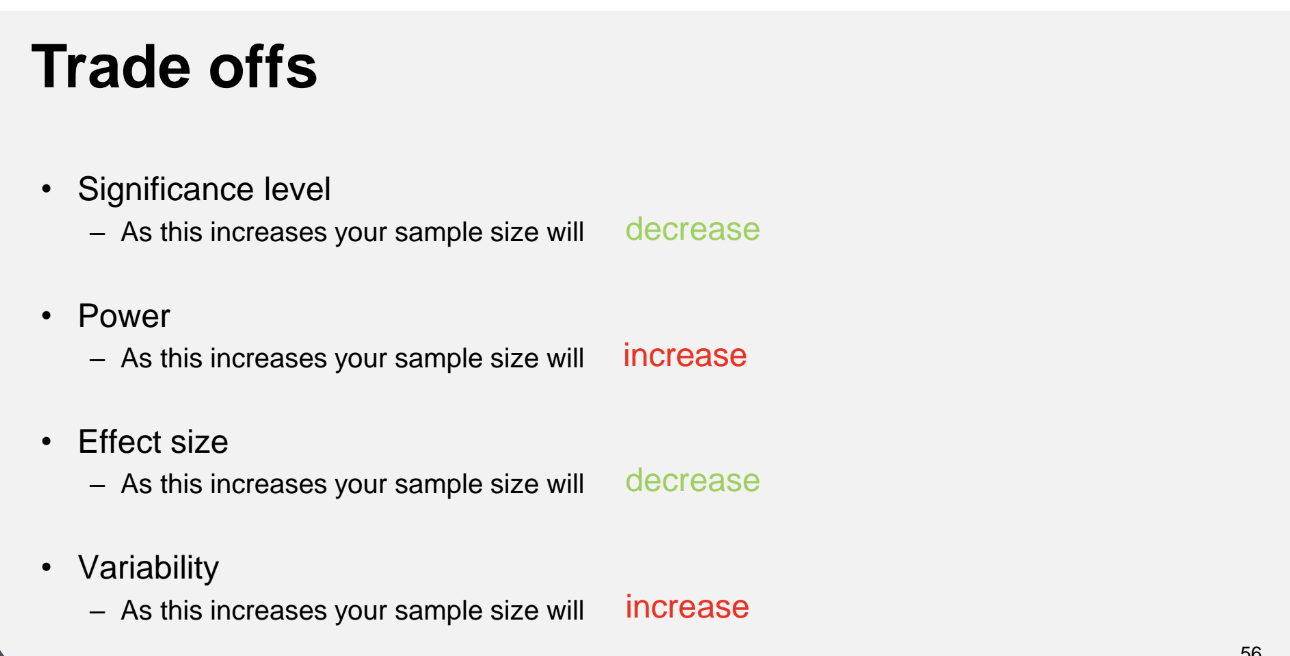
Key Factors Affecting Sample Size

1. Significance level (α)

2. Statistical Power (1 - β)

3. Effect size (Δ)

4. Variability (σ²)

Formula for Continuous Outcomes

• Function f(α, β) = applied values of significance and power.

Example: PROMPT Study

• Treatment: Two types of platelet transfusions.

• Outcome: Platelet increments.

Sample Size for Binary Outcomes

• Function for proportions in groups: [ n_{group} = \frac{\pi_1(1 - \pi_1) + \pi_2(1 - \pi_2)}{(\pi_2 - \pi_1)^2} f(α, β) ]

Summary

• Explained randomisation methods to ensure treatment groups do not differ systematically.

• Discussed stratification and minimisation to balance patient characteristics.

• Emphasized the importance of blinding to reduce bias in clinical trials.

• Detailed sample size calculations that account for effect size and variability.