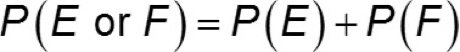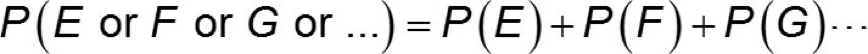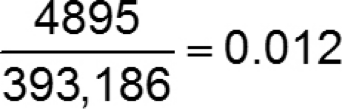5.2 Addition Rule and Complememnts (AND FLASHCARDS WITH HW)
Disjoint is also called ‘Mutually Exclusive’
What does it mean when two events are disjoint?
They have no outcomes in common
Another word for “disjoint” is “mutually exclusive”
So, events can be called disjoint or mutually exclusive
Venn Diagram Tool
Rectangle = Sample space
Each circle = An event
Use letters “E” and “F” represent each event.
Label it in the circle.
Here is an example of what a Probability Venn Diagram should look like
EX: Suppose we randomly select a chip from a bag where each chip in the bag is labeled 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Let E represent the event “choose a number less than or equal to 2,” and let F represent the event “choose a number greater than or equal to 8.” These events are disjoint as shown in the figure.
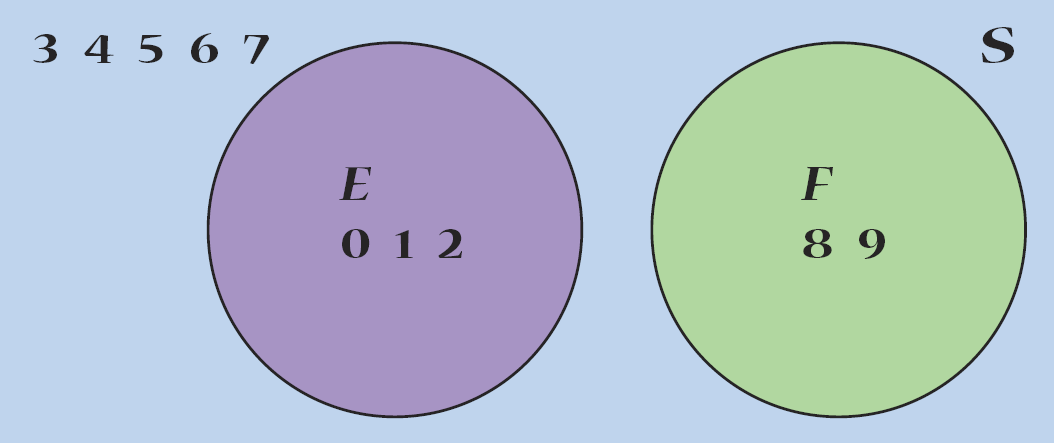
How to calculate a single event’s probability:
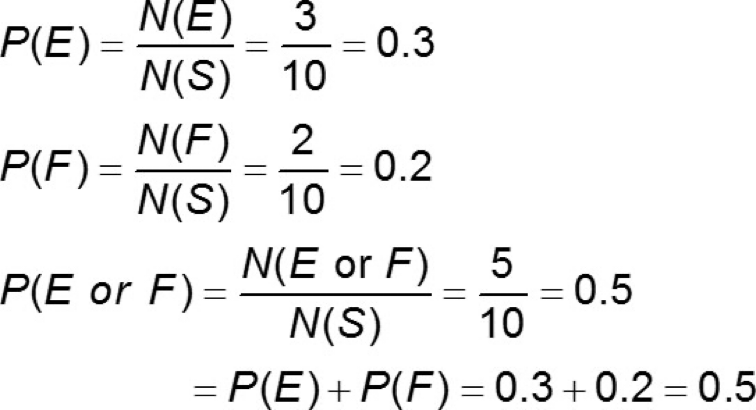
“Disjoint” means “mutually exclusive” and describes the relationship between events:
In probability, "disjoint" is synonymous with "mutually exclusive," which means that only one of the events can happen at a given time.
Disjoint (or mutually exclusive) events are those that cannot happen at the same time, or have different values— so, only one of the events can happen at a given time. Note, events may be considered disjoint if they have different valuess; the key definition of disjoint events is that they cannot happen simultaneously.
Example: If you flip a coin, getting heads and getting tails are disjoint events because you can only get one result on a single flip.
Key takeaway: If two events happen at the same time, regardless of their values being different, they are not considered disjoint events.
The Addition Rule is used to calculate the probability that either (or both) of 2 or moew events will happen. The addition rule has two formulas, one for mutually exclusive events and one for non-mutually exclusive events:
1. The Addition Rule for Mutually Exclusive (Disjoint) Events
These are for Events that cannot happen at the same time.

Statement: “If two events, A and B, are disjoint (meaning they have no common outcomes/cannot occur at the same time), then the probability of either/both event A or event B happening is simply the sum of their individual probabilities”
Two events:
If two events ( E and F) are disjoint, then the probability of either one of them is found by…
Three or more events:
If (E, F, G, … ) are all disjoint, then the probability for all of them is found by….
EXAMPLE Addition Rule for Mutually Exclusive (Disjoint) Events
The probability model below shows the distribution of the number of rooms in housing units in the United States.
(a) Verify that this is a probability model.
(b) What is the probability a randomly selected housing unit has two or three rooms?
(c) What is the probability a randomly selected housing unit has one or two or three rooms?
Number of Rooms in Housing Unit | Probability |
One | 0.010 |
Two | 0.032 |
Three | 0.093 |
Four | 0.176 |
Five | 0.219 |
Six | 0.189 |
Seven | 0.122 |
Eight | 0.079 |
Nine or more | 0.080 |
Part (a) steps:
All probabilities are between 0 and 1 (inclusive)
This means they all add up to 1
0.010 + 0.032 + … + 0.080 = 1
Minitab function to sum probabilities:
Calc > Column Statistics…
Make sure “sum” is selected
Make sure proper column is in “Input Variable”.
Part (b) steps:
P(two or three)
= P(two) + P(three)
= 0.032 + 0.093
= 0.125
Part ( c ) steps:
P(one or two or three)
= P(one) + P(two) + P(three)
= 0.010 + 0.032 + 0.093
= 0.135
2. Addition Rule for the probability of Non-Disjointed (Non-Mutually Exclusive) Events.
Used when events can happen separately and/or may occur at the same time (i.e.,events overlap is possible)
calculated by adding the probabilities of event E and event F, then subtracting the probability of both events occurring simultaneously (the overlap between E and F)
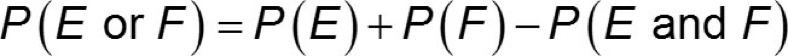
The subtraction of P(A and B) prevents double counting.
EXAMPLE Identifying a Non-Disjointed Event
According to a center for disease control, the probability that a randomly selected person has hearing problems is 0.158. The probability that a randomly selected person has vision problems is 0.094. Can we compute the probability of randomly selecting a person who has hearing problems or vision problems by adding these probabilities? Why or why not?
No, because hearing and vision problems are not mutually exclusive. So, some people have both hearing and vision problems. These people would be included twice in the probability.
Some people have both hearing and vision problems. This means that the events of having a hearing problem and having a vision problem are not disjoint (or not mutually exclusive). Remember, when two events are not disjoint the General Addition Rule must be used, where the probability is found by adding together the two given probabilities and subtracting the probability of a person having both problems. If the probability of a person having both problems is not subtracted out, then these people will be included twice in the probability.
How to find components of each parts above^^^
Where N(E) is the number of outcomes in E and N(S) is the number of outcomes in the sample space.
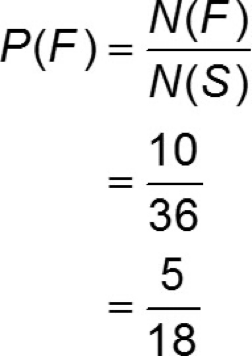
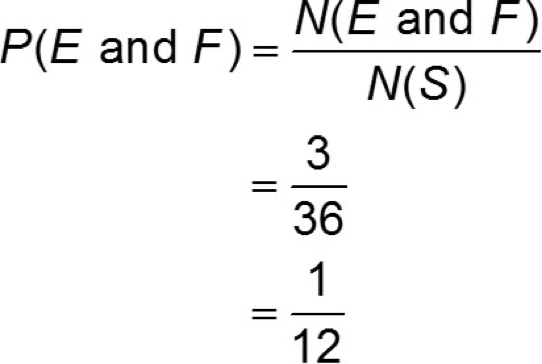
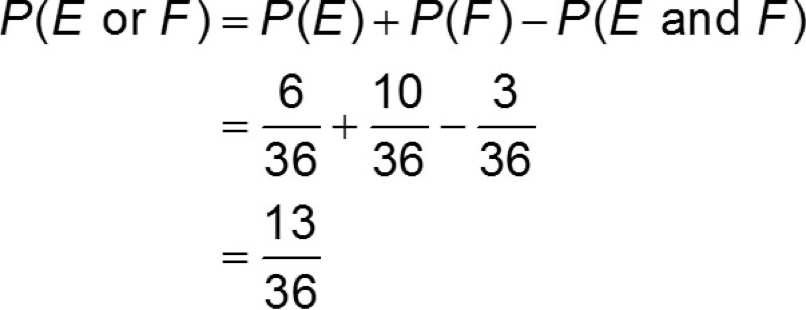
Probability of a Disjoint Event Using the Complement Rule
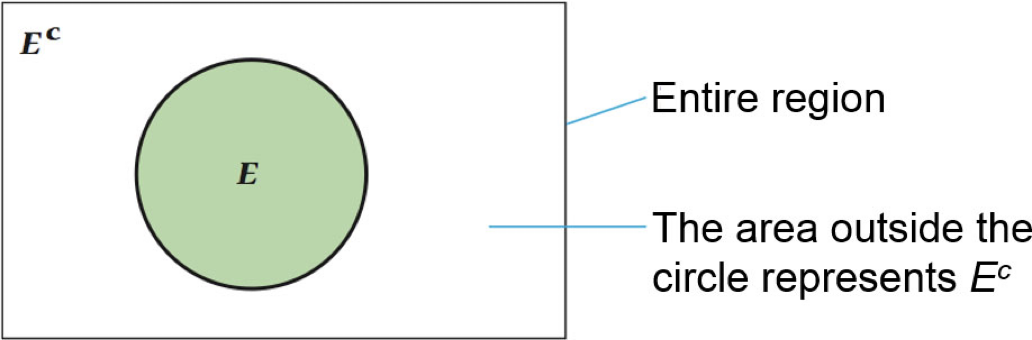
Complement of an Event (EC ) is the subset of outcomes in the sample space that are NOT in the event.
The Complement Rule
If E represents any event and EC represents the complement of E, then
P(EC) = 1 – P(E)
Key Knowledge
is the subset of outcomes in the sample space that are NOT in the event.
Is itself an event.
An event and its complement are always mutually exclusive (they cannot occur simultaneously) and exhaustive (one of the two events must occur).
Calculating Probability: To find the probability of an event's complement, subtract the probability of the original event from 1.
Example: If event A is "rolling a 6 on a standard dice," then the complement of A would be "rolling any number other than a 6".
Complement of Event = EC
EXAMPLE Illustrating the Complement Rule
According to the American Veterinary Medical Association, 31.6% of American households own a dog.
(a) What is the probability that a randomly selected household does not own a dog?
P(do not own a dog) = 1 − P(own a dog)
= 1 − 0.316
= 0.684
EXAMPLE Illustrating the Complement Rule
The data to the below represent the travel time to work for residents of Hartford County, CT.
Travel Time | Frequency |
Less than 5 minutes | 24,358 |
5 to 9 minutes | 39,112 |
10 to 14 minutes | 62,124 |
15 to 19 minutes | 72,854 |
20 to 24 minutes | 74,386 |
25 to 29 minutes | 30,099 |
30 to 34 minutes | 45,043 |
35 to 39 minutes | 11,169 |
40 to 44 minutes | 8,045 |
45 to 59 minutes | 15,650 |
60 to 89 minutes | 5,451 |
90 or more minutes | 4,895 |
(a) What is the probability a randomly selected resident has a travel time of 90 or more minutes?
There are a total of 24,358 + 39,112 + … + 4,895 = 393,186 residents in Hartford County.
The probability a randomly selected resident will have a commute time of “90 or more minutes” is…
(b) Compute the probability that a randomly selected resident of Hartford County, CT will have a commute time less than 90 minutes.
P(less than 90 minutes) = 1 − P(90 minutes or more)
= 1 − 0.012 = 0.988