4 Colligative Properties

1. Osmotic pressure

2. Lowering of vapor pressure

3. Depression of freezing point

4. Elevation of boiling point

Freezing Point Depression

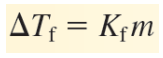
• ΔT = difference between the initial freezing point of the pure solvent and the final freezing point

• Kf = freezing point depression constant for the solvent (°C/m)

• m = concentration (mol solute/kg of solvent) of the solution in molality

Molarity (M) & Molality (m)

• Molarity = (moles of solute)/(liters of solution)

• Molality = (moles of solute)/(mass of solvent in kg)

• Molality is the number of moles of solute dissolved in 1 kg (1000g) of solvent

What advantage does Molarity have over Molality?

• Molarity is great for measuring exact volumes

What advantage does Molality have over Molarity?

• Molality is temperature independent (i.e. concentration does not change with temp.)

Freezing Point Depression Non-Electrolytes

• Non-electrolytes do not dissociate into “pieces” of the formula units.

• Ex: Sugar (a non-electrolyte) molecules will dissolve in water but will not come apart into many pieces in water. Therefore, one mole of sugar molecules in a solution will yield one mole of dissolved sugar molecules.

Van’t Hoff Factor (i)

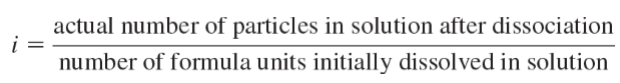Electrolyte Solutions

Using the van’t Hoff factor in the calculation accounts for the multiple moles of ions that go into solution when ionic compounds dissociate into their constituent cations and anions

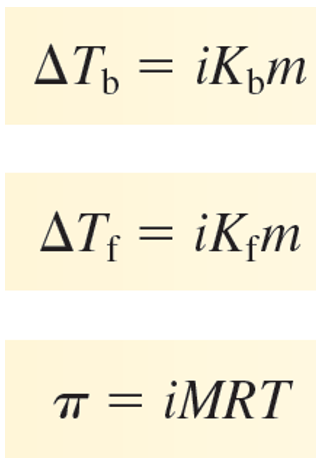
Effect of Adding a Solute

1. Decrease the solvent’s freezing point.

2. Increase the solvent’s boiling point

The degree of freezing point depression is related to the identify of the solvent, the molar mass of the solute, and the mass of the solution. This relationship is expressed as: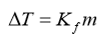

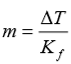
1. ΔT = difference between the initial freezing point of the pure solvent and the final freezing point

2. Kf = freezing point depression constant for the solvent (-1.86°C/m)

3. m = molal concentration (mol solute/kg of solvent) of the solution

2nd formula allows the determination of the number of moles of solute present

Molar mass = number of grams of solid initially weighed / number of moles of solute determined in the experiment