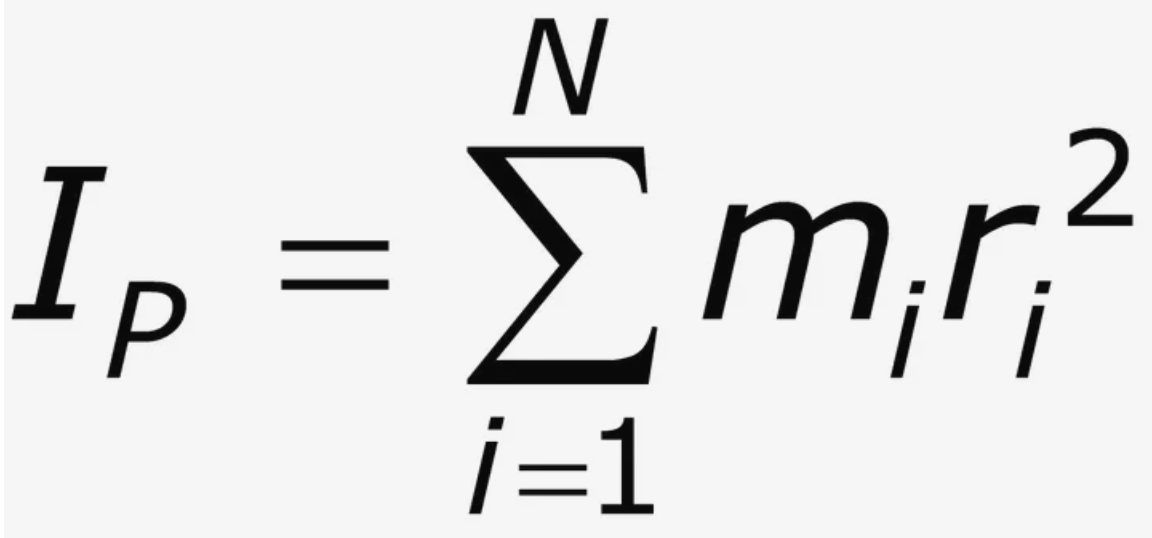Center of mass - average position of all the parts of a system

• using coordinates

  • 

• Position vector for center of mass

  • 

  • where m is the mass of the object, M is total mass of system, and r is the position vector

  • Units: distance units (m, cm, etc.)

• Velocity of center of mass

  • find by dividing total momentum by total mass of system

Rotational Kinematics

• Angular displacement - the angle in radians through which a point has been rotated

  • 

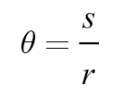
  • Units: radians

• Angular velocity - how fast an object rotates

  • angular velocity (w) = change in theta/change in time

  • 

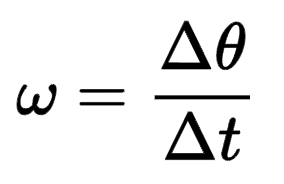
  • Units: rad/sec or revolutions

  • If angular velocity is negative, then rotation is clockwise

  • If angular velocity is positive, then rotation is counter clockwise

• Average Angular acceleration - change in angular velocity of a rotating object

  • also called rotational acceleration

  • angular acceleration = change in angular velocity/change in time

  • 

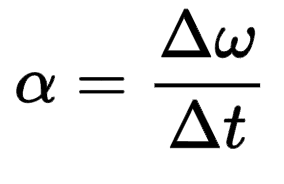
  • Units: rad/s²

  • Instantaneous angular acceleration is the derivative of angular velocity with respect to t, (dw/dt)

• Tangential velocity - linear speed of a rotating object

  • at every point while the object is rotating, it has a velocity tangential to the path of rotation at that point

  • 

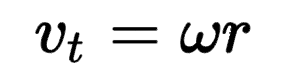
  • Units: m/s

• Tangential acceleration - rate of change of tangential velocity of a rotating object

  • 

  • Units: rad/s²

• Radial acceleration - the acceleration of a rotating object to the center of the circle

  • 

  • Units: rad/s²

• Rotation with constant acceleration equations

  

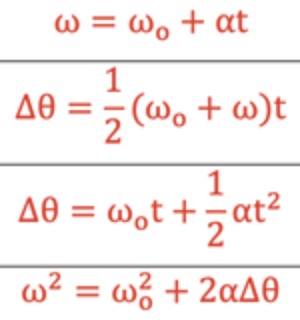
• Rotational Kinetic Energy - kinetic energy due to the rotation of an object

  • 

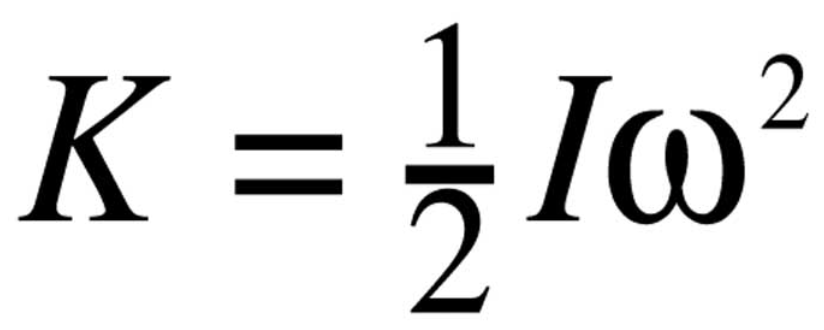
  • where (I) is the moment of inertia of the object above its axis of rotation

  • Units: J

Moment of Inertia - the torque required to change an object’s angular acceleration

• general formula

  • 

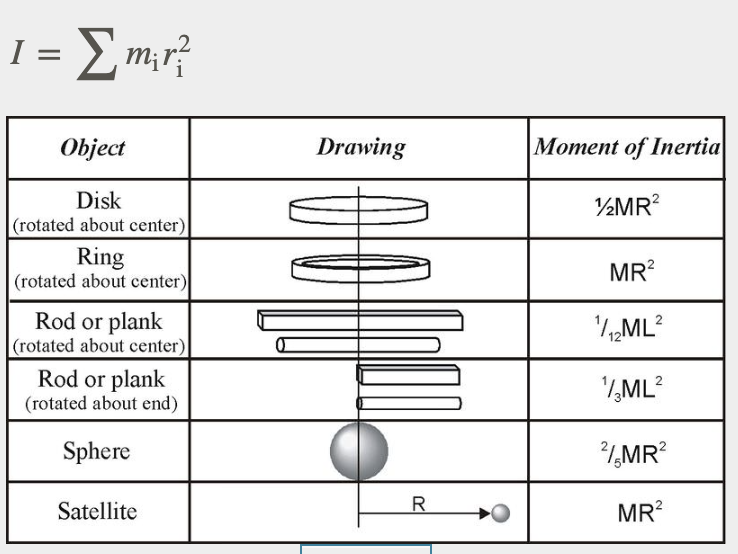
• an object has a larger moment of inertia if it has more mass, or more mass distributed further away from the axis of rotation (its easier to rotate)

• an object has a smaller moment of inertia if it has less mass, or it mass is distributed closer to the axis of rotation (its harder to rotate)

• Units: kg·m²

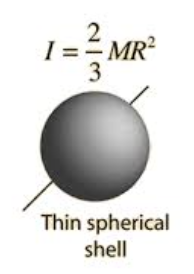
Moment of inertia of objects with mass

Torque - tendency of rotation. the rotational equivalent of a force

• torque = (Force) · (lever arm)

• torque = I (a)

  

• lever arm is the perpendicular distance from the axis of rotation to the force’s line of action

• if the lever arm is at an angle then the perpendicular distance can be found with the formula in the image above

• Unit: N·m

• vector so it has both magnitude and direction

• torque is positive (+) if rotation is counter-clockwise

• torque is negative (-) if rotation is clockwise

Simple Harmonic Motion

• An object moves with SHM if its acceleration is proportional to its displacement but points in the opposite direction

• Period - the time for one complete oscillation

  • 

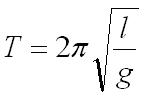
  • Units: seconds (s)

• Frequency - the number of oscillations per second

  • 

  • Units: Hz

• Amplitude - the maximum distance the object is from equilibrium

  • 

  • 

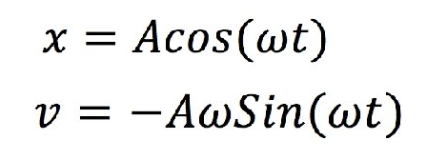
  • w = sqrt(k/m)

  • where k is the spring constant and m is the mass