Lecture 2 Financial Mathmatics 1

FINC2011 Topic Two: Financial Mathematics

Aim of financial mathematics

  • Aim of Financial Mathematics

    • Convert cash flows to a single value.

    • Represents the value of cash flows from an asset or liability.

    • Used for:

      • Making rational choices between options.

      • Determining intrinsic value of an asset.

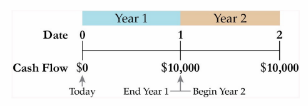
Cashflows Timeline

  • Drawing a Timeline

    • Linear representation of cash flow timing.

    • Inflows (+) and outflows (-).

Three Rules of Time Travel

  • Rule 1: Compare values only at the same time.

  • Rule 2: Compound to move cash flows forward in time.

  • Rule 3: Discount to move cash flows backward in time.

Rule 1: Comparing Values

  • Cash flows must be at the same point in time for comparison.

  • Future value FV measures the value of cash flows at the end of a specific period, representing at time N.

  • Present value PV measures the value of future cash flows at the beginning of a specific period, representing at time0.

Rule 2: Compounding Cash Flows

  • Compounding to find Future Value:

Rule 3: Discounting Cash Flows

  • Discounting to find Present Value:

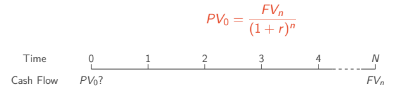
    Higher n, the less it is worth in present time. Higher r, lower present value.

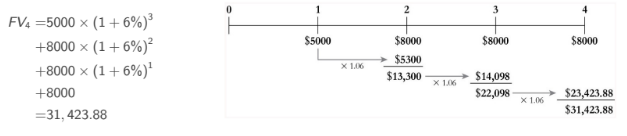
Stream of multiple cash flows

  • Valuing a Stream of Cash Flows

    • Apply single cash flow formulas to multiple cash flows.

    • Present Value of a Cash Flow Stream formula.

    • same thing can be achieved for FV.

Why is there constant payments over time?

  • A company must make a stream of constant payments on a bank loan for a period.

  • Individual investors may make constant payment on a home or car loans or invest a fixed amount year after year saving for retirement.

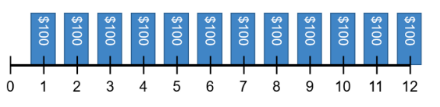
Annuities

If there is a series of cash flows that satisfy these conditions, there is an annuity:

  • Finite life, regular intervals, constant payment amounts.

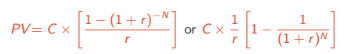
Ordinary Annuity vs. Annuity Due

Ordinary annuity: cash flows at the end of each period.

Annuity due: cash flows at the beginning of each period.

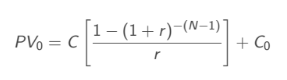
Annuity due formula

FV Annuities

  • FV of Annuities

    • Future value calculations for savings or investments.

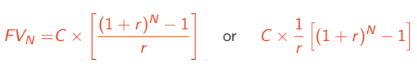
Note: the FV will give the value at the time of the lasat payment, there is a cash flow at time N, but none at time 0.

Perpetuity

  • Perpetuities

    • A stream of constant cash flows that foes on forever.

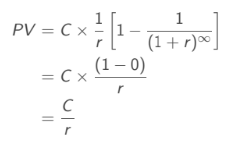
Using the same conditions from annuity, the only differences is the timeline:

  1. Infinite life

  2. Regular payment intervals

  3. Constant dollar value of payment

Growing perpetuity

  • Growing Perpetuities

    • Present value formula for growing perpetuities.

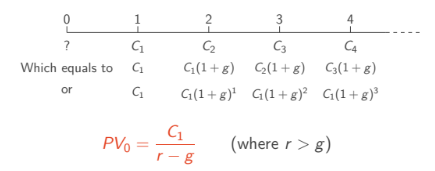
Growing Annuity

  • PV of Growing Annuities

    • Present value formula for growing annuities.

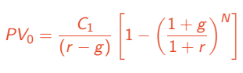
Deferred annuity

  • Deferred Annuity

    • Basically cash flows with delays, apply all the above theory to use for calculating this.

      can calculate PV then discount it.

How does managers make invest decisions?

By using net present value NPV, accept those investment with positive NPV: