PY 131 Chapter 19: Vibrations and Waves

Harmonic Motion

Yet another form of motion is called harmonic or periodic motion

• a.k.a. an oscillation or vibration.

An object moves over the same path repeatedly. Examples of harmonic motion include:

• a pendulum
• mass on a spring
• floating bob

Consider a mass attached to a compressed spring.

• a) Equilibrium position is at x = 0. Velocity is not zero.
• c) Velocity has changed sign.
• d) At x = +A or -A the velocity is zero.

The maximum distance from the equilibrium position, here it is A, is called the amplitude.

In SHM the displacement, the velocity, and the acceleration all follow sine curves.

The Period and Frequency

• The period is the amount of time it takes the system to cycle through one oscillation.
• The frequency f is the inverse of the period.
  • f =1/T
• The SI unit of frequency is hertz, the symbol is Hz.

The Pendulum

• Small oscillations of a pendulum are another case of SHM.

• The longer the pendulum the longer the period.

  

  

EXAMPLE 1:

A pendulum has period T on Earth. If the same pendulum were moved to the Moon, how does the new period compare to the old period?

• Since the gravity is smaller on the Moon, it will take a ==longer period.==

EXAMPLE 2:

Two pendula have the same length, but different masses attached to the string. How do their periods compare?

• ==They are the same.== The period only depends on length and acceleration to to gravity (g). We see this in the equation 2(pi) x sqrt(L/g).

Waves

• The general description of a wave is that it is a moving disturbance of some quantity around its equilibrium.
• Waves and harmonic motion are closely related: both involve oscillations around an equilibrium.
  • In some cases a wave can be modeled as a large number of coupled oscillators – one oscillator affects the next.
• While a classical wave can be localized i.e. confined to a region in space, they are not ‘objects’ - they do not have a mass.
• However, a wave transfers energy and momentum (and sometimes angular momentum) without transport of mass.
• Examples of waves include:
  • surface water waves (water height),
  • earthquakes – sound waves in a solid
  • waves on a spring or string (string height, spring compression),
  • sound (air pressure),
  • light (E and B fields),
  • gravitational waves (spacetime deformations),
• Except for a few cases, waves need a medium – a material substance in stable equilibrium which can be distorted.
  • Such waves are called mechanical waves.
  • The medium itself does not undergo translational motion – the medium oscillates around its stable equilibrium.
  • in some cases - e.g. water waves, the medium does move, but the velocity
    of the medium is much slower than the velocity of the wave.

Types of Waves

• Waves can be divided into two types called transverse and longitudinal.

  • there are some waves which are mixtures of both e.g. water waves.

• For transverse waves, the disturbance is perpendicular – transverse – to the wave motion.

• For longitudinal waves the disturbance is in the same direction as the wave motion.

• Some media can support both types of wave.

• 

• Waves are also divided into wave pulses (or pulse waves) which are disturbances localized in space, and periodic waves (harmonic waves) where the disturbance is spread out in space.

  • There is a gray (grey) area in between when waves are sometimes called wavepackets.

  

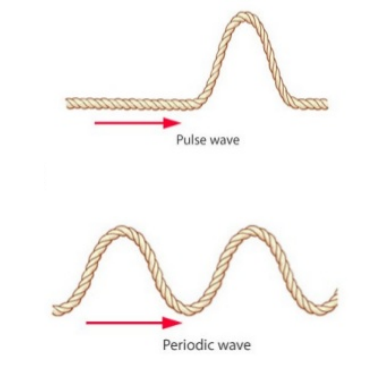
Harmonic Waves

• A harmonic wave is one that repeats in space and time.

• At a fixed point in space, the disturbance in the medium will also oscillate with the same period as the wave passes by. A

• t a fixed time, the disturbance will be periodic in space.

• At a fixed time, the disturbance as a function of distance from the source, will look something like

  

• The amplitude A is the 'height' of the wave – the maximum deviation from the equilibrium.

• The distance between successive identical points on the wave – e.g. between adjacent crests – is called the wavelength λ.

• At a fixed point in space, the disturbance as a function of time will also look something like:

  

• The period T is the amount of time it takes to cycle through one oscillation.

• The frequency f is the number of oscillation cycles per unit time which pass by a fixed point

  • f =1/T

• The wave velocity is the ratio of the distance traveled by a feature on the wave, e.g. a crest, and the time elapsed.

  

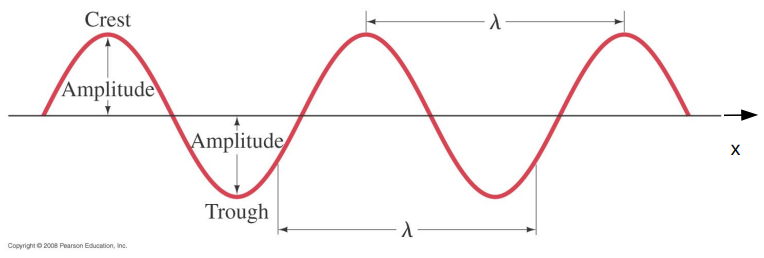
• It takes one period T for the wave to move one wavelength λ.

• The wave velocity (phase velocity) is v=λ/T=λ f

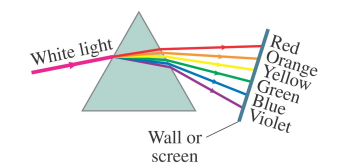
• In some cases the wave speed does depend upon the frequency. This effect is called dispersion. This effect is used by a prism to 'split' white light: the speed of light in the glass is different for each color.

• 

• In the ocean, long wavelengths travel faster than short wavelengths.

• The velocity of the wave is different from the velocity of the medium.

• 

Wave Creation

• Waves are generated by vibrating objects. If the source oscillator has a period T then it produces a wave with a period T.

EXAMPLE 1:

Does a longitudinal wave, such as a sound wave, have an amplitude?

• Yes. Every wave has an amplitude.

EXAMPLE 2:

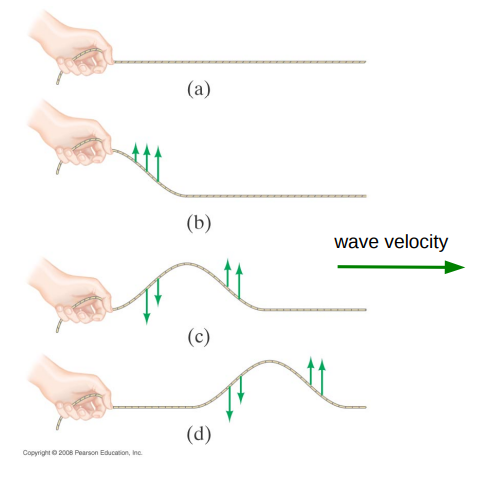
Consider a wave on a string moving to the right. What is the motion of point A?

• 
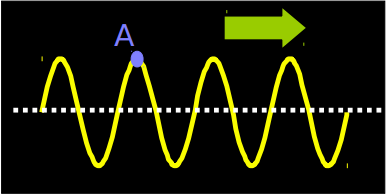
• ==Up and down== (not left and right)

EXAMPLE 3:

Consider point B on the string What is the velocity of point B? B

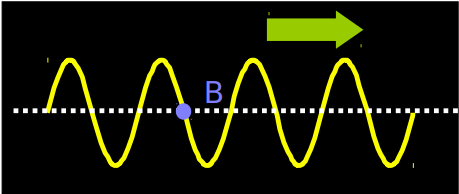
• It’s moving in the positive direction, so to the ==right.==

2D and 3D Waves

• In 2D and 3D we can have more kinds of waves.

  • the kind which is most similar to waves in 1D are called plane waves.
  • in 2D and 3D there also exist circular waves and spherical waves.

• Wavefront – lines in 2D or 3D which connect the same feature on the wave e.g. a crest.

• Ray – a line in the direction of wave motion and perpendicular to the wavefronts.

  

• The amplitude of circular and spherical waves decreases with distance from the source.

• The reason a wave in 2D and 3D attenuates is because of conservation of energy.

• All waves transport energy at a rate which varies as the square of the amplitude.

• The energy passing through a circle (2D) or sphere (3D) surrounding the source must be constant.

  • in 2D we must have 2π r A^2= constant
  • and in 3D we must have 4π r^2 A^2 = constant

• In 2D the amplitude must vary as A ∝1/√r.

• In 3D the amplitude must vary as A ∝1/r.

  

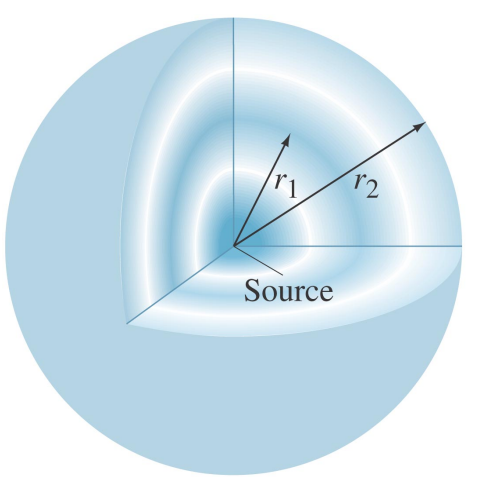
A1 r1=A2 r2

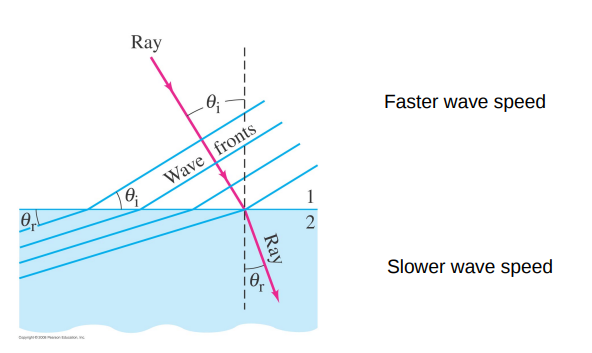
Reflection and Transmission

• When a wave reaches a boundary with a medium that has a different wave speed, some of the wave is reflected and some is transmitted.

  • Exactly what happens depends upon whether the wave speed increases or decreases.

  

• For a wave in 1D the reflected wave simply propagates in the reverse direction.

• In 2D and 3D the direction the reflected wave propagates depends upon the angle at which it hit the boundary.

• At every point upon a boundary we can draw a line perpendicular to the surface called the normal.

• The angle between the incoming ray and the normal – called the angle of incidence – is equal to the angle between the reflected ray and the normal – the angle of reflection.

• This relationship is called the Law of Reflection.

  \n

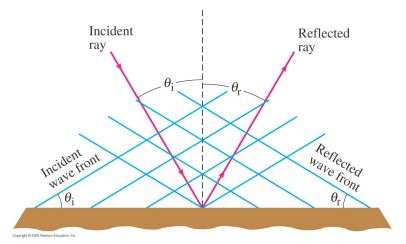
• That part of the wave which is not reflected is transmitted.

• In 1D the transmitted wave continues in the same direction as the incident wave.

• In 2D and 3D the direction the transmitted wave propagates depends upon the angle at which is strikes the surface.

• This effect is called refraction.

  

  

Diffraction

• If a wavefront is partially blocked by an obstacle, the unblocked part of the wavefront spreads into the shadow region behind the obstacle. This effect is called diffraction.
  • Diffraction is the reason you can hear a source around a corner

EXAMPLE 1:

A wave travels faster in a thin rope than in a thick rope (if the tension is the same in both). A wave traveling along a thin rope meets and enters a thick section of rope. Which property of the wave in the thick rope is the same as in the thin rope?

• ==Same frequency and period.==
  • The frequency of the wave remains the same since it is determined by the source of the wave. The wavelength of the wave may change, depending on the change in the wave speed and the frequency. Since the tension is the same in both the thin and thick ropes, the wave speed is primarily determined by the linear mass density of the rope (μ). Therefore, when the wave enters the thick section of the rope, its speed decreases due to the increase in the linear mass density of the rope.

The Principle of Superposition

• Unlike objects, two or more waves can exist at the same point in space at the same time. The net disturbance at a given point in space is the sum of the disturbances of the individual waves.

  • This is called the principle of superposition.

  

Interference

• When two waves pass through each other, the net disturbance at some point in space follows the principle of superposition.

• The two waves are said to interfere.

• If the net disturbance is greater than the disturbance of either wave separately the interference is constructive.

• If the net disturbance is less than the maximum disturbance of the two waves, the interference is destructive.

  

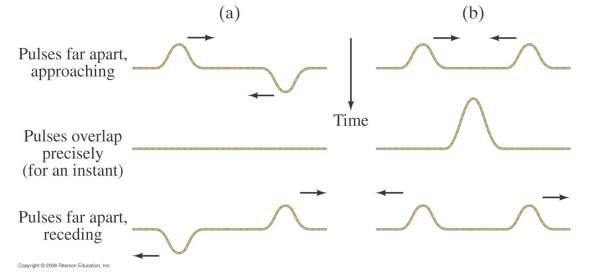
• More generally, for waves in 1D we have three situations:

  

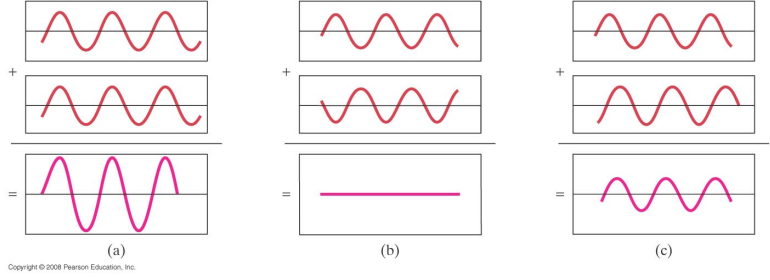
• Synonymously we use in phase to mean constructive interference and out of phase to mean destructive

• In 2D and 3D the interference between two circular/spherical waves depends upon the distance from the sources.

  

• Consider two coherent sources of sound waves with the same frequency. The net sound wave at a given location depends upon the distance from that point to the sources.

  

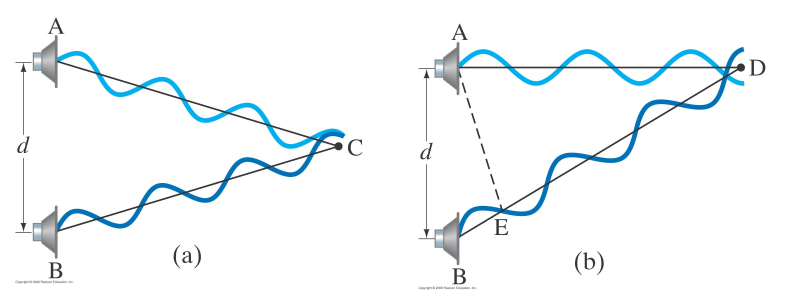
• If the difference in distance to the sources is an integer number of wavelengths then the waves constructively interfere.

• If the difference in distance to the sources is half-integral then the two waves destructively interfere.

Standing Waves

• It is possible to set up a vibrating medium where the wave appears to be standing still.

  • i.e. a crest does not move left or right, its velocity is zero.

• The system can be decomposed into two waves traveling in opposite directions which interfere

  • Typically one of the waves is a reflection of the other.

• At some places the two waves constructively interfere, at other they destructively interfere.

• At special frequencies of the two waves the locations of destructive and constructive interference are fixed.

• These locations are called nodes and antinodes respectively.

  • Since the nodes and antinodes do not move, the net wave appears to be stationary.
  • The sounds made by musical instruments can be understood in terms of standing waves.

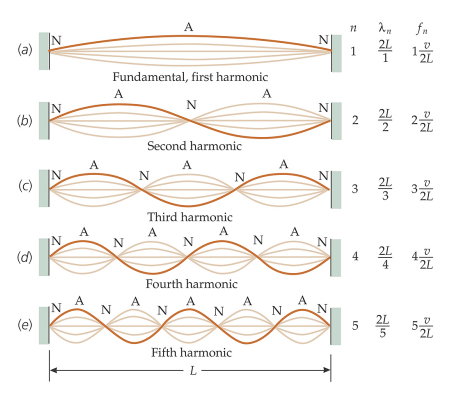
• The most common example of this phenomenon is a taut string.

  

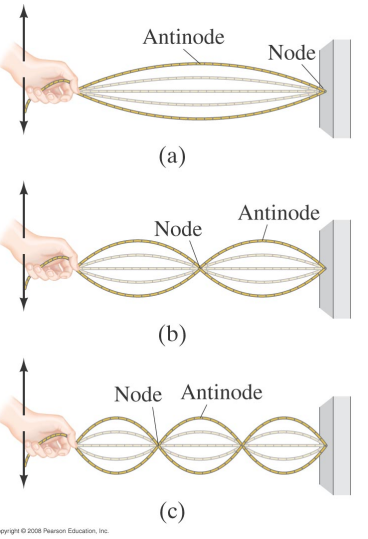
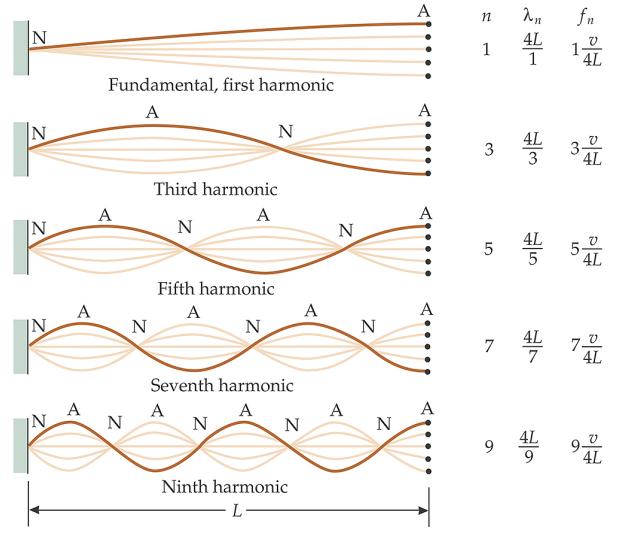
• For a string of fixed length, only certain wavelengths can produce standing waves.

  

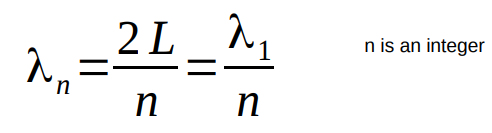
• Knowing the wave velocity, the frequencies can be found

  

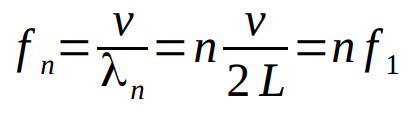
• The lowest frequency, f1, is called the fundamental.

• The higher allowed frequencies are called overtones.

• When the overtones are multiples of the fundamental, the overtones are also called harmonics.

  

• Now let's consider a taut string of length L which is fixed only at one end while the other end at is able to move. The fixed end point corresponds to the location of a node: the free end is an antinode. Again, only certain wavelengths of the standing wave can fulfill this condition.

  

Doppler Effect

• If a source is moving with respect to an observer, the frequency is perceived to be different than when there is no relative motion.

• If the source is moving towards an observer the frequency appears to be higher than when the source and observer are at rest.

• If the source is moving away from an observer the frequency of the sound wave appears to be lower.

  

• This change in perceived frequency is called the Doppler Effect.

Moving Source, Stationary Director

• The change in frequency depends upon whether the source or receiver is stationary with respect to the medium.

• Consider a source located one wavelength from a receiver.

  

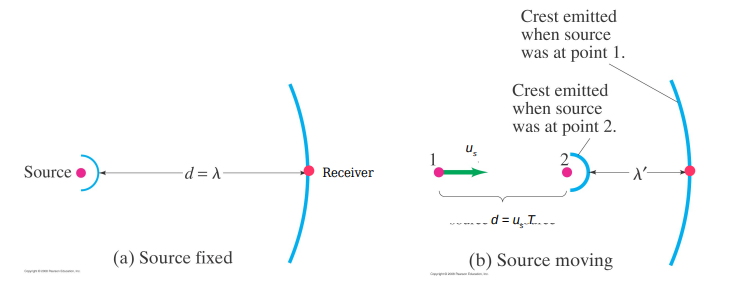
• When the source moves toward the receiver the wavelength of the wave in that direction shrinks.

  

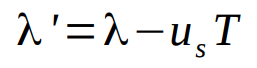
Stationary Source, Moving Detector

• The Doppler effect also occurs when the source is stationary and the detector moves.

• If the detector moves towards the source the receiver perceives a shorter time period T' for the wave.

  

  

Double Doppler Shifts

• Consider the case where a stationary source emits a wave towards an object moving toward the source.

  

• The object perceives the wave to have a higher frequency because it is moving towards the source.

• The object reflects a wave (i.e. it becomes a source) with the same (higher) perceived frequency.

• The original source perceives the reflected wave to have an even higher frequency because the object is moving toward it.

• The Doppler Effect also occurs for light. Astronomers use the Doppler Effect to measure the speed of an object towards or away from Earth.