Understanding Functions

3.1: Graphing Relationships

• Vocabulary:

  • Continuous graph- represent real-world situations that are drawn without any interruptions made up of connected lines or curves.

  • Discrete graphs: are made up of distinct, unconnected points.

Continuous vs. Discrete with Examples

• Domain: Represents all the x values

• Range: Represents all the y values

  • Range depends on Domain

Video Explanation: Graphing Relationships and Interpreting Graphs

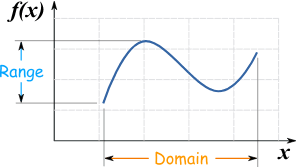
3.2: Understanding Relations and Functions

• Vocabulary

  • Relation: a set of ordered pairs (x, y) where x is the input value and y is the output value.

  • Function: type of relationship in which there is only one output value for each input value

  • Vertical line test: a relation is a function if a vertical line does not pass through more than one point on the graph of the relation

  • Domain: Represents all inputs

  • Range: Represents all outputs

    • Range depends on Domain

    • Y depends on x

3.3: Modeling Functions

• Vocabulary

  • Independent Variable: The input of a function (Domain)

  • Dependent variable: The output of a function (Range)

  • Function notation: If x is the independent variable and y is the dependent variable, then you can use function notation to write y = ƒ(x), which is read “y equals ƒunction of x,” where ƒ names the function

  • Function Rule: An algebraic expression that defines a function

3.4: Graphing Functions
There are a few different ways to write the equation of a line. One of the most common ways is called the "slope-intercept" form.  It's called this because it clearly identifies theslope and the y-intercept in the equation.  The slope is the number written before the x.  The y-intercept is the constant written at the end.

How To Graph a Line in Slope-Intercept Form

• Step 1: Identify and plot the y-intercept.

  • The constant written at the end is the y-intercept of the graph.  This tells you where to begin your graph.

• Step 2: Identify the slope and use it to plot the 2nd point.

  • The slope is the number in front of the x.  Remember, the slope is rise/run.

    • If it's positive, go up and to the right.  If it's negative, go down and to the right.