Demonstrate understanding of mechanical systems - External, 6 credits

Translational Motion

A Vector quantity has a magnitude and a direction, while a Scalar quantity only has a magnitude.

Vector components are drawn as arrows. We add vectors head-to-tail. At Level 3, three vector quantities will form a right-angled triangle which we can then solve for each component and its angle. The hypotenuse of this triangle is the resultant vector. Trigonometry (SOH CAH TOA) or Pythagoras’ Theorem can be used to find these values.

Momentum (p) is a quantity that all moving objects have. The greater the momentum, the more impact the object will have when it collides with another object. In a collision, momentum must be conserved. This means that:

$p_{in}=p_{out}$

Momentum can be found using:

$p=mv$ , and it is measured in $kg\space{ms^{-1}}$

Momentum is a vector quantity, in the same direction as the velocity. An external net force acting on an object will change its momentum. The formula for this is:

$\Delta{p}=p_f-p_i$

As with other vector quantities, momentum components can be added as a right-angled triangle to see the result of a collision or explosion.

Newton’s Three Laws of Motion:

1. When the resultant force on an object is zero, there is no acceleration. The object will either be stationary or moving in a straight line at a constant speed. This is known as inertia.

2. When an unbalanced force acts on an object, it causes acceleration. The acceleration is proportional to the size of the force and inversely proportional to the mass of the object. This gives us:

   $F=ma$

3. For every action there is an equal and opposite reaction. E.g. when a tennis player hits a ball with their racquet, a force is applied to the ball, while a force of equal magnitude in the opposite direction will act on the racquet.

The Centre of Mass of an object is where the mass acts from. In a uniform object (e.g. a planet), the centre of mass will be in the middle. In a non-uniform object (e.g. a broom), the centre of mass will be the point where the mass on each side exerts an equal torque on the object. A system of objects also has a centre of mass. The centre of mass of a system of two or more objects can be found using:

$x_{COM}=\frac{x_1m_1+x_2m_2}{m_1+m_2}$

For a system of objects that are spread over a plane, the x and y co-ordinates of their positions can be calculated using the same formula, then added together as co-ordinates (x, y). The distance between the objects can be found using trigonometry.

When objects in a system are moving, momentum is conserved. As there is no change in mass, there will also be no change in overall velocity. This means that the centre of mass of the system will remain unchanged.

Circular Motion and Gravitation

In Circular Motion, an object moving at a constant speed will be accelerating (changing velocity), due to its changing direction. This is own as centripetal acceleration, or acceleration towards the centre of the circle. The centripetal acceleration can be found using $a_c=\frac{v²}{r}$. This can be substituted into $F=ma$, giving $F_c=\frac{mv²}{r}$ - the centripetal force acting on the object.

In a conical pendulum setup, an object is swung on the end of a string in a circle. If there is no friction, the speed and radius of its motion will be constant. A free-body force diagram gives the following quantities:

• Weight force = $mg$

• Vertical component: $mg=T\cos(\theta)$

• Horizontal component ($F_c$): $\frac{mv²}{r}=T\sin(\theta)$

Where $T$ is the tension force provided by the string.

When an object is travelling around a banked corner, the centripetal force is increased, which helps to travel safely around the corner at a high speed. Assuming the banked corner is frictionless, the centripetal force must equal the horizontal component of the reaction force. The speed when this occurs is called the critical speed. The following quantities can be obtained from a free-body force diagram：

• Weight force = $mg$

• Normal force: $F_N=\frac{mg}{\cos(\theta)}$

• Horizontal reaction force: $F_R=F_N\sin(\theta)=mg\tan(\theta)$

The normal force acts at $90^o$ to the angle of banking ($\theta$).

These equations can be combined to find the critical speed:

$\frac{mv²}{r}=mg\tan(\theta)\\v=\sqrt{gr\tan(\theta)}$

If travelling too fast around a banked corner, the object has a higher velocity so the radius of its turning circle will increase (moves to the outside of the corner). If travelling too slow around a banked corner, the object has a lower velocity so the radius of its turning circle will decrease (moves to the inside of the corner). However, the normal force will still act at $90^o$ to the surface.

Vertical Circular Motion describes the motion of objects under the influence of both a tension force and gravity, which add to give a centripetal force that varies based on the position of the object in its circular path. At the top of the path, the centripetal force is smallest, as the tension force is zero, so $F_c=F_g$. At the bottom of the circle, the centripetal force is the largest, and tension force is more than double the weight force (F_T>2F_g).

When an object is travelling over a rise, $F_{net}=F_g-F_R$. At slow speeds, the reaction force is slightly less than the weight force acting on the object. The higher the speed, the less reaction force acts upon the object. At the maximum speed, the reaction force is zero, and $mg=\frac{mv²}{r}$. When travelling faster than the maximum speed, the object will act as weightless, as there is not enough weight force to maintain the circular path. The maximum speed can be found using:

$mg=\frac{mv²}{r}\\v=\sqrt{\frac{g}{r}}$

As the object completes one rotation, it undergoes some energy transformations.

Gravitation describes how large bodies (such as planets) affect one another. The equation for gravitation is:

$F=\frac{Gm_1m_2}{r²}$ , where $F$ is the force, $m_1$ and $m_2$ are the two masses, $r$ is the radius of the system, and $G$ is the gravitational constant, $6.67×10^{-11}\space\frac{Nm²}{kg²}$

For a satellite, the gravitational force is the centripetal force holding it in orbit. From this we can derive:
$\frac{mv²}{r}=\frac{Gm_1m_2}{r²}$

$v=\sqrt\frac{Gm_2}{r}$, where $m_1$ is the mass of the satellite (which cancels out)and $m_2$ is the mass of the planet.

Rotational Motion

Pure Rotational Motion is created when an object spins around its centre of mass, due to two equal forces acting on opposite sides of the object.

Angular Displacement ($\theta$) is the angle that the object has rotated through. The translational distance travelled is found using $d=r\theta$, where $r$ is the radius. Note that $\theta$ is measured in radians.

Angular Velocity ($\omega$) is found using $\omega=\frac{\Delta\theta}{\Delta{t}}$ , and is measured in radians per second ($rad s^{-1}$). The translational velocity of the object can be found using $v=\omega{r}$.

Angular Acceleration ($\alpha$) is the rate of change of angular velocity, found using $\alpha=\frac{\Delta\omega}{\Delta{t}}$. The translational acceleration can be found using $a=\alpha{r}$. When the angular acceleration is constant, the four equations of motion for rotating systems can be derived:

$\omega_f=\omega_i+\alpha{t}$

$\theta=\frac{1}{2}(\omega_f-\omega_i)t$

$\omega_f²=\omega_i²+2\alpha\theta$

$\theta=\omega_i{t}+\frac{1}{2}\alpha{t}²$

The Moment of Inertia or Rotational Inertia of an object describes its resistance to change in motion. It varies based on the mass of the object, the radius of the object, and how the mass is distributed throughout the object. An object with mass concentrated in the centre will have a low moment of inertia while an object with mass concentrated along the edges will have a high moment of inertia.

Torque ($\tau$) is a force that causes an object to rotate. A torque applied to a body causing it to rotate can be found using $\tau=Fr$. Torque is measured in Newton metres ($Nm$). In translational motion, the force and acceleration are linked by $F=ma$, while in rotational motion they are linked by $\tau=I\alpha$.

Newton’s Laws of Motion can also be applied to rotating systems:

1. The Law of Inertia: An object in motion maintains constant angular velocity unless acted on by an external net torque.

2. $\tau_{net}=I\alpha$ links the moment of inertia and the acceleration of an object in rotational motion.

3. When an object exerts torque on another object, the object will simultaneously exert a torque of equal size and opposite direction to the torque acting on it.

Rotational Kinetic Energy can be found using $E_{K(Rot)}=\frac{1}{2}I\omega²$. A rotating system may have both rotational and translational kinetic energy, in which case the equations can be combined:

$E_{K(Tot)}=\frac{1}{2}mv²+\frac{1}{2}I\omega²$

As energy is conserved, assuming no losses due to friction, the gravitational potential energy that an object has will be converted entirely into kinetic energy. The ratio of rotational to translational kinetic energy depends on the radius of the object, as mass cancels out in the equation:

$mg\Delta{h}=\frac{1}{2}mv²+\frac{1}{2}I\omega²$ (as $I$ is made of the mass and radius of the object).

An object rolling down a ramp has both rotational and translational kinetic energy. The time taken to reach the bottom of the ramp depends on the translational acceleration of the object. Therefore, if more kinetic energy is translational than rotational, the object will accelerate faster, thereby reaching the bottom of the ramp faster. As an object with a higher moment of inertia will have more mass distributed further away from its centre of mass, it will accelerate more slowly, as more of its potential energy is converted to rotational than translational kinetic energy.

Angular Momentum (L) can be found using $L=I\omega$, and is measured in $kgm²s^{-1}$. Translational and rotational kinetic energy can be linked using $L=mvr$, or $I\omega=mvr$. Angular momentum must be conserved. In order to increase the angular velocity of a rotating system, the moment of inertia must be decreased. During rotational collisions or explosions, energy must be conserved. If the energy before the collision or explosion is not the same as the energy after, then work must have been done to remove energy from or add energy to the system.

Simple Harmonic Motion

Simple Harmonic Motion (SHM) is oscillatory motion where there is a changing acceleration. Motion is proportional to displacement. A restoring force causes acceleration towards the equilibrium point, meaning that it is in the opposite direction to the displacement.

There are three main types of SHM:

1. Pendulum on a string → side-to-side movement

2. Particle in longitudinal wave (e.g. ocean waves) → up and down movement

3. Mass on a spring → up and down movement

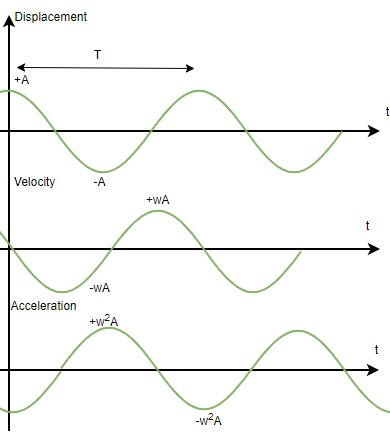
The Equilibrium Point (EP) is the point where displacement is zero, and there is maximum velocity and no acceleration

The Amplitude (A) is the distance furthest from the equilibrium point. This is where there is maximum displacement and acceleration and velocity is zero.

The Time Period (T) is the amount of time taken to travel from one amplitude, to the other, and back to the first. It is found using $T=\frac{1}{f}$, where frequency is measured in $s^{-1}$ or $Hz$.

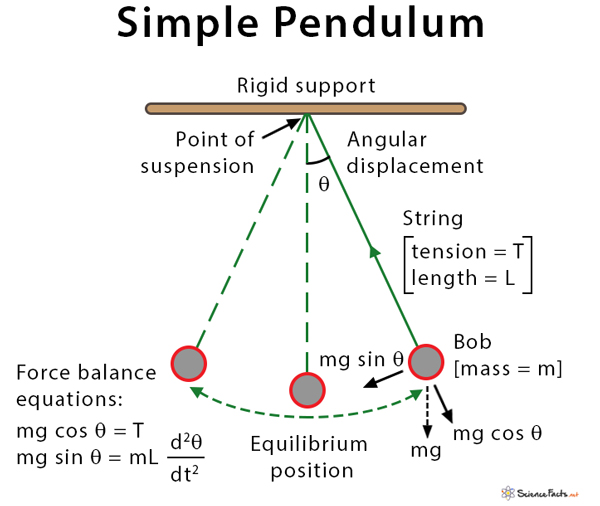
A simple pendulum contains a mass suspended at the end of a string of negligible mass. When pulled back, the mass will undergo SHM. The time period is dependent only on the length of the string:

$T=2\pi\sqrt{\frac{l}{g}}$ , where $l$ is the length of the string and $g$ is gravity.

The mass will experience a number of forces:

• Gravity, acting straight down. The force of gravity is constant throughout the motion of the mass.

• Tension force, along the string. The tension force can be found using $F_T=mg\cos(\theta)$ , where $\theta$ is the instantaneous angle that the string is at. Because the angle is constantly changing throughout the motion, the value of the tension force will also constantly change.

• Restoring force, pulling the mass towards the equilibrium point. The restoring force can be found using $F_R=mg\sin(\theta)$, where $\theta$ is the instantaneous angle that the string is at. Because the angle is constantly changing throughout the motion, the value of the restoring force will also constantly change. The restoring force is always in the opposite direction to the motion of the mass.

A mass bouncing on a spring will also experience SHM, as long as the spring does not fully close, or the mass travels beyond the spring’s limit. The period is dependent on the mass on the spring and the spring constant:

$T=2\pi\sqrt\frac{m}{k}$

A very large spring constant represents a heavy spring, while a small spring constant represents a light spring. The spring constant is measured in $N m^{-1}$. The restoring force on a spring can be found using $F=-kx$, and the elastic energy stored in a spring is found using $E=\frac{1}{2}kx²$.

When two identical springs in parallel have a mass attached undergoing SHM, the weight force will be distributed over the two springs so there will be less extension. As $F=-kx$, the spring constant of the system is increased. When two identical springs in series have a mass attached undergoing SHM, the weight force will act fully on each spring, resulting in a larger extension. This means that the spring constant of the system is decreased. Spring constants in parallel are added $k_{total}=k_1+k_2…$ while spring constants in series are added $\frac{1}{k_{total}}=\frac{1}{k_1}+\frac{1}{k_2}…$. In relation to one $25Nm^{-1}$ spring, two identical springs in parallel will have double the spring constant $(50Nm^{-1})$ and half the extension, while two identical springs in series would have half the spring constant $(12.5Nm^{-1})$and double the extension. As the time period for oscillation is dependent only on the mass and period, not the extension, identical springs in parallel will have the shortest period and two springs in series will have the greatest period.

When an object undergoes SHM, its displacement will resemble a sine wave, its velocity will resemble a cosine wave, and its acceleration will resemble a negative sine wave. This is due to kinematics, as the function is differentiated each time:

$d=Asin(\omega{t})\\v=\omega{A}cos(\omega{t})\\a=-\omega²{A}sin(\omega{t})$ where $d$ is displacement, $v$ is velocity and $a$ is acceleration. These are graphed: