Chapter 9: Rotational Dynamics

9.1: The Action of Forces and Torques on Rigid Objects

• Pure translational motion: all points on an object move in parallel paths.

• General motion: combination of translation and rotation.

• Torque: a turning force causing angular acceleration. Mag of force x lever arm

  • Equation: \tau =Fl

  • SI unit: N\cdot m

• Torque amount depends on:

  • Where and in what direction the force is applied.

  • Axis of rotation.

• Maximum turning occurs farthest from the axis of rotation.

• Counterclockwise rotation = positive torque

• Bigger the lever arm, bigger the torque

• Lever arm: the distance from the axis of rotation to the line of action of the force.

• Line of action: runs through force vector that is creating the torque. Extends in both directions

9.2: Rigid Objects in Equilibrium

• Rigid body equilibrium:

  • Zero translational acceleration.

  • Zero angular acceleration.

• Equilibrium conditions:

  • Sum of externally applied forces is zero.

    • \Sigma F_{x}=0

    • \Sigma F_{y}=0

  • Sum of externally applied torques is zero.

    • \Sigma \tau =0

• Reasoning Strategy

  • Choose the object for equilibrium analysis.

  • Draw a free body diagram showing all external forces.

  • Select suitable x, y axes and break forces into components along these axes.

  • Apply equilibrium equations: Set net forces in x and y directions to zero.

  • Choose a convenient axis of rotation. Set sum of torques about this axis to zero.

  • Solve equations for desired unknowns.

Static Equilibrium (exam written response)

• Stillness and Balance: Static equilibrium means something isn't moving and is balanced. It's like when you're sitting perfectly still in a chair without tipping over.

• Force and Torque Balance: To stay still, everything pushing or pulling on the object must balance out. This includes both forces (like pushing or pulling) and torques (like twisting forces).

• Three Conditions: For static equilibrium, three things must be true:

  • All the forces on the object add up to zero.

  • All the twisting forces on the object add up to zero.

  • The object doesn't start moving or rotating on its own.

• Real-Life Examples: Static equilibrium is important in designing stable buildings, bridges, and other structures. It helps engineers make sure things don't collapse or fall over.

• Stability: Objects can be stably balanced (like a bowl sitting still), unstably balanced (like a pencil standing on its tip), or neutrally balanced (like a ball sitting in a bowl).

9.3: Center of Gravity

• Center of gravity: point where an object's weight effectively acts when calculating torque.

• If an object is symmetrical shape and uniform, the center of gravity lies at its geometrical center.

• Equation: x_{cg}=\dfrac{W_{1}x_{1}+W_{2}x_{2}}{W_{1}+W_{2}}

  • More can be added on ff more weights are presents.

9.4: Newton’s 2nd Law for Rotational Motion About a Fixed Axis

Tangential Forces

• Tangential force: F_{T}=ma_{T}

• With substitution for F_{T} and a_{T}

  • \tau =\left( mr^{2}\right) \alpha

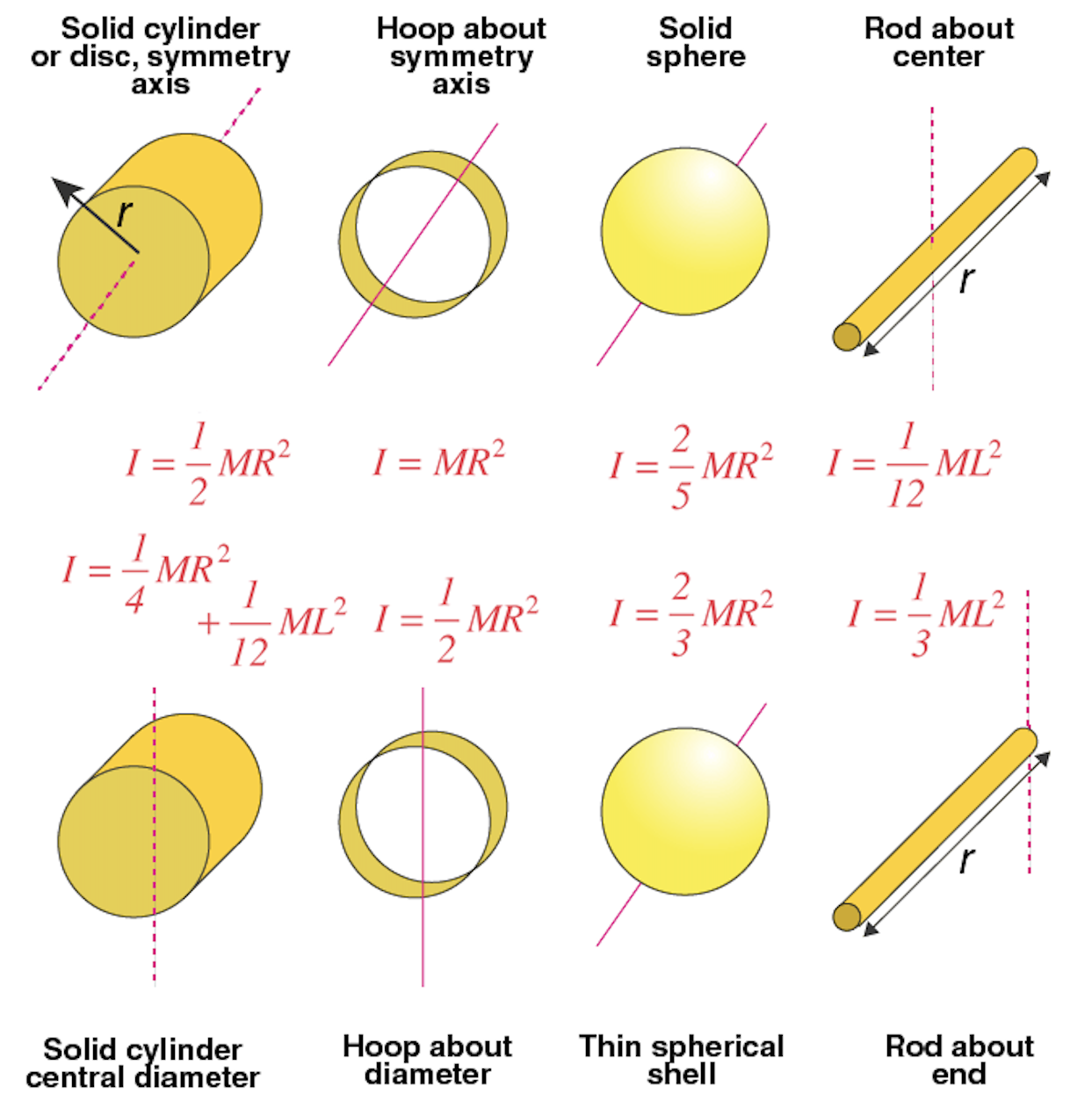
Moment of Inertia

• Inertia: the tendency of an object to resist changes in its motion.

• Moment of inertia for a single point mass:

  • Equation: I=mr^{2}

  • Inertia can only be zero or positive

• Greater moment of inertia corresponds to increased resistance for an object's motion.

• If you have a weird shape being spun around an axis, the moment of inertia of that axis is going to be basically the sum of the moments of inertia of all the point masses that make up that object.

  • Equation: \Sigma \tau=\sum \left( mr^{2}\right) \alpha

    • \tau _{1}+\tau _{2}+\tau _{3}

Rotational Analog

• Net external torque = (Moment of inertia)x(Angular acceleration)

• Equation: \Sigma \tau =I\alpha

• SI unit: kg\cdot m^{2}

• Requirement: Angular acceleration must be expressed in radians/s²

Moment of Inertia - Shapes

9.5: Rotational Work and Energy

• Rotational work: the energy transformation that occurs when rotating objects experience torque over a distance (results in change in rotational KE).

  • Equation: W_{R}=\tau \theta

    • \theta =\dfrac{s}{r}

  • SI unit: J

  • Scalar quantity

  • Requirement: The angle must be expressed in radians

• Rotational kinetic energy: the energy a rigid object has due to its rotation.

  • Equation: KE_{R}=\dfrac{1}{2}I\omega ^{2}

  • SI unit: J

  • Scalar quantity

• Total kinetic energy = KE_{tota1}=\dfrac{1}{2}I\omega ^{2}+\dfrac{1}{2}mv_{T}^{2}

• Mechanical energy of a rotating object: E=\dfrac{1}{2}mv^{2}+\dfrac{1}{2}I\omega ^{2}+mgh

  • Transitional KE + Rotational KE + PE

• Energy Conservation:

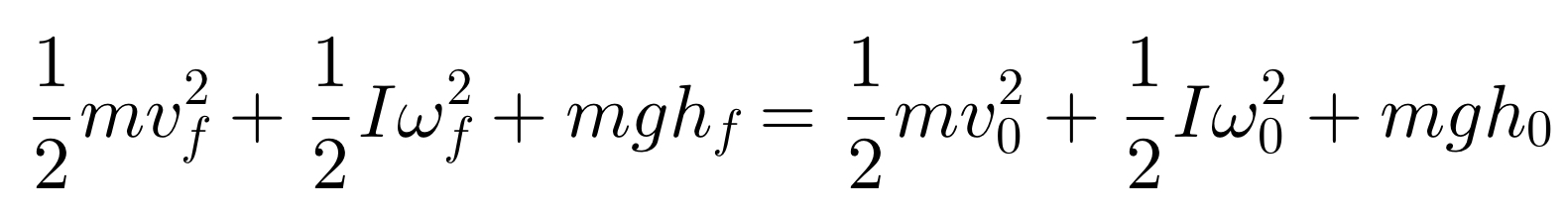
9.6: Angular Momentum

• Angular momentum: the product of an object's moment of inertia and its angular velocity around the same axis.

• Equation: L=I\omega

• SI unit: kg\cdot m^{2}/s

• Requirement: The angular speed must be expressed in rad/s

• Principle of Conservation of Angular Momentum:

  • The angular momentum of a spinning system remains constant (is conserved) if the net external torque acting on the system is zero.

  • Example: Ice skater spinning