🎀Unit 2 AP Calculus AB Review Guide🎀

Secant Lines and Average Rate of Change

• Example problem: What is the slope of the secant line that intersects the the graph of 4x+1 at x=0 and x=6?

• The first step in solving these types of problems is to plug in the provided x-values into this equation.

• 4(0)+1=1

• 4(6)+1 = 35

• The second step of this problem is to set up the equation by plugging it into the equation we use to find average rate of change. f(6)-f(0)/6-0 = 35 - 1/6-0 = around 5.67. Therefore, the final answer is 5.67.

Derivative as a slope of a curve

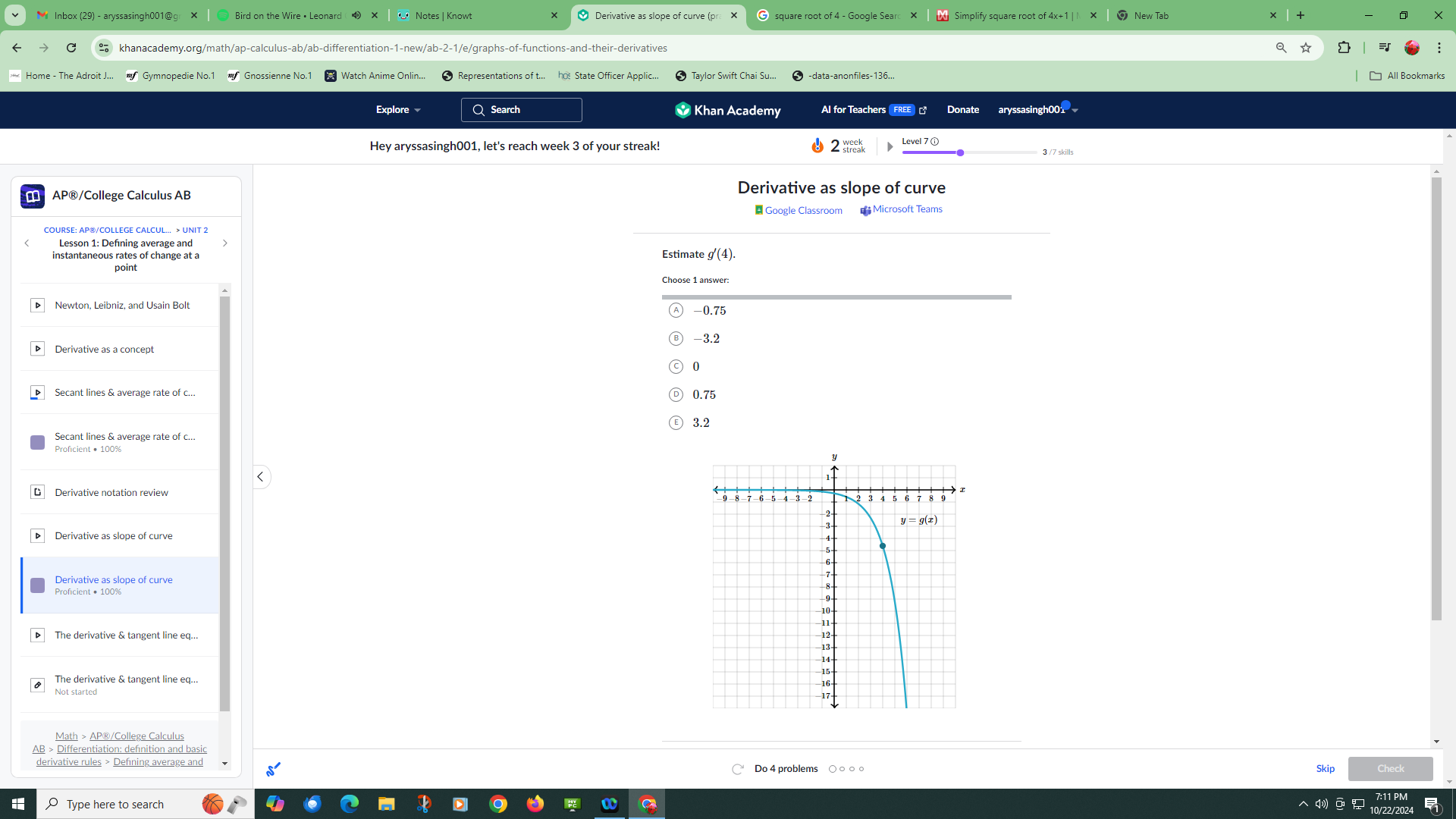
To see the image more clearly, just open it up in a new tab . To find the derivative using a graph, look at the direction of the graph at that point. This will already help us eliminate some answers, as we can see that at that point at the graph, the direction is pointing downwards, which means we can eliminate the positive answers. Then, imagine a line that touches the graph at g(4) only. This line has a negative slope thats close to three, which is why -3.2 is the correct answer to this question.

The derivative and the tangent line:

-Example problem: the tangent line to the graph of the function at the point (1,5) passes through the point (3,4). Find g’(1)

-All you have to do is find the slope using the formula y2-y1/x2-x1!

4-5/3-1= -1/2: this is our final answer

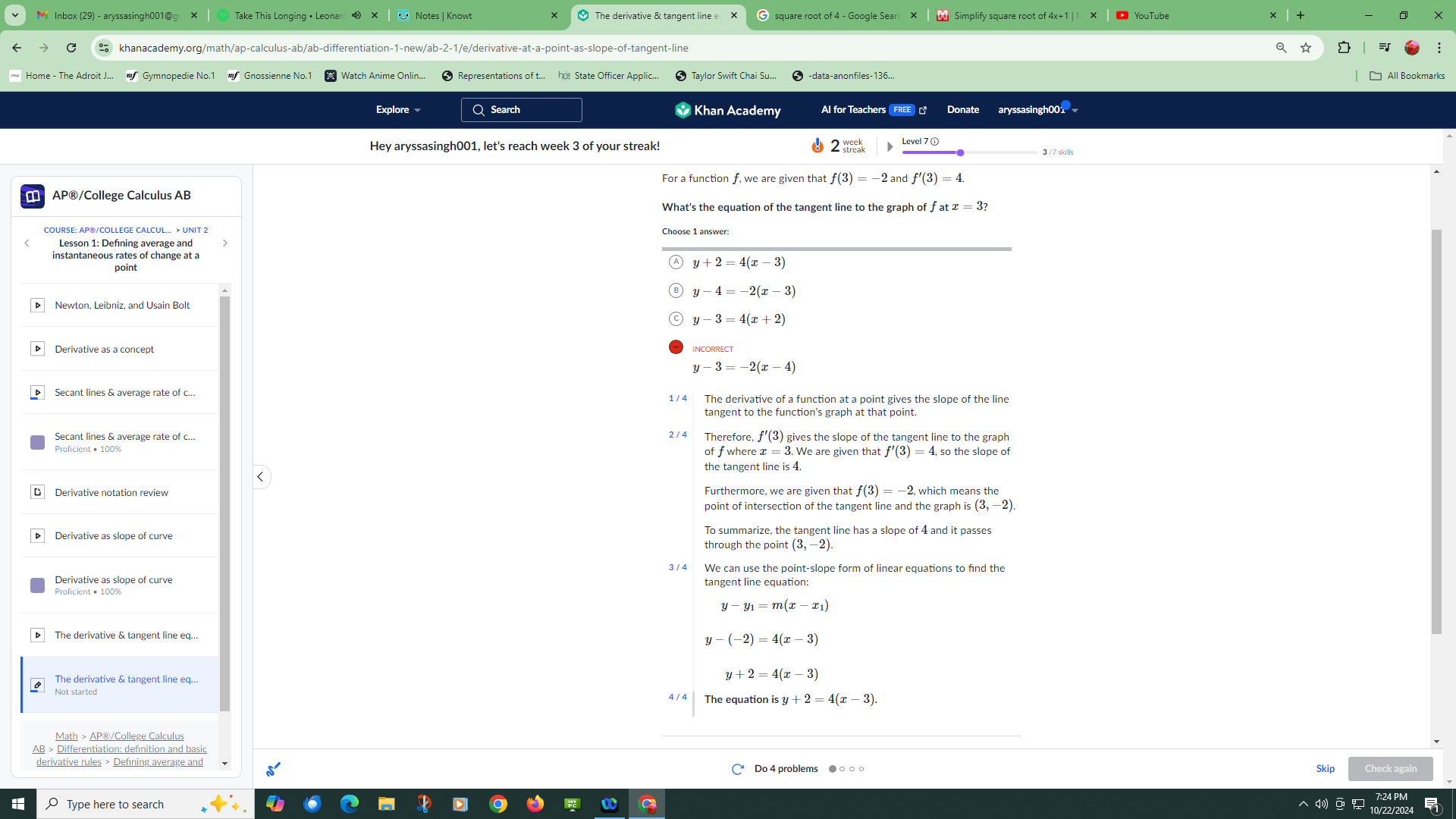
-For some problems you might have to make an equation in point slope form. You will do this by creating an x y table and using the point slope formula to work it out. An example of this type of problem is shown below.

Find derivatives using limits

Example problem: f(x)=3x²+12

-The equation wel’ll use is as the limit of h approaches zero f(x+h)-f(x)/h if the limit exists. This means that f’(x) = lim as h approaches zero. This means that you will plug in the numbers in this equation by putting in (x+h) anywhere there is an x.

This will give you 3(x+h)²+12 - (3x²+12)/h = 6x when simplified completely. The h’s always cancel out. If they don’t cancel out you didn’t do this correctly.

Estimating Derviatives

to do this, pick two numbers-one larger than the number and one smaller, but they still have to be close to the derivative. then plug those in to the average rate of change formula we used for the first example problem in this guide.