Hydrology Notes

INFILTRATION

• Infiltration is the process of water penetrating into the soil.

Factors Affecting Infiltration Rate

1. Condition of the soil surface

2. Vegetative cover

3. Soil properties

   • Porosity

   • Hydraulic conductivity

   • Moisture content

Unsaturated and Saturated Flow

• Unsaturated flow: Flow through a porous medium when some voids are occupied by air.

• Saturated flow: Occurs when voids are filled with water.

Water Table

• Interface between saturated and unsaturated flow.

• Atmospheric pressure prevails at the water table.

• Saturated flow occurs below the water table, and unsaturated flow occurs above it.

Control Volume Analysis

• Consider a control volume with sides of lengthsdx, dy, and dz, having a volume of dxdydz.

• The volume of water contained is \theta dxdydz. Where \theta is not defined in the document.

Darcy Flux

• Darcy flux - Flowthrough the control volume

• Defined as q = \frac{Q}{A}where Q is the volumetric flow rate and A is the soil area.

Darcy's Law

• Relates Darcy flux (q) to the rate of head loss per unit length of medium.

• For vertical flow, the head loss per unit length is the change in total head (\delta h) over a distance (\delta z), i.e., \frac{\delta h}{\delta z}.

• Expressed as q = -K \frac{\delta h}{\delta z}, where K is hydraulic conductivity.

Unsaturated Flow Characteristics

• Void spaces are partially filled with water.

• Water is attracted to particle surfaces through electrostatic forces.

• Suction head (\psi) - is the energy due to soil suction forces. (use average)

• Total head (h) - is the sum of suction and gravity heads: h = \psi + z.

• Darcy's law for unsaturated flow:

  q = -K \frac{\partial(\psi + z)}{\partial z}.

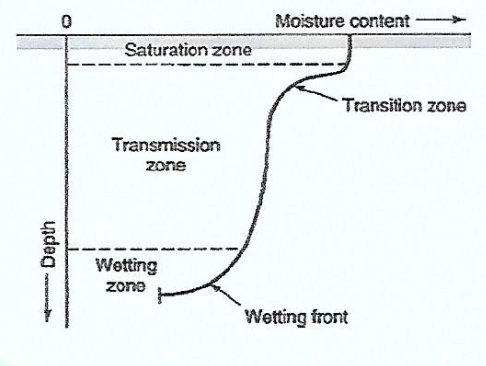
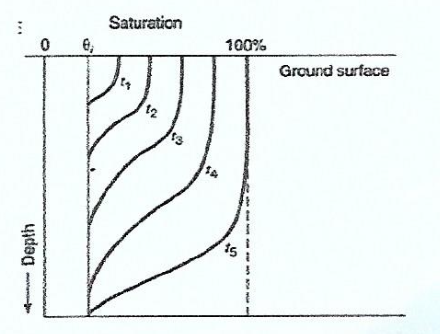
Green Ampt Method

• Describes soil moisture distribution during downward movement.

Moisture Zones

Infiltration Rate

• f: Rate at which water enters the soil surface (in/hr or cm/hr).

• Potential infiltration rate: Rate when water is ponded; actual rate is less if no ponding.

Cumulative Infiltration

• F: Accumulated depth of water infiltrated.

• Expressed as F(t) = \int_{0}^{t} f(x) dx.

• Infiltration rate: f\left(t\right)=\frac{dF\left(t\right)}{dt} .

Rainfall Hyetograph

• Illustrates rainfall pattern as a function of time.

• Increase in cumulative infiltration from time t to t + \Delta t is F(t + \Delta t) - F(t).

• Rainfall excess: Rainfall that is neither retained nor infiltrated.

Green and Ampt Model

• Simplified infiltration model.

• Wetting front: Sharp boundary dividing soil with moisture content \theta_i below and saturated soil with porosity n above.

• Wetting front has penetrated to depth L in time t.

• Water is ponded to a small depth h_0 on the surface.

Vertical Column of Soil

• Consider a unit horizontal cross-sectional area.

• Moisture content increases from \theta_i to n as the wetting front passes.

• Increase in water stored: L(n - \thetai) = L\Delta\theta = F, where \Delta\theta = n - \thetai.

• Cumulative infiltration: F(t) = L(n - \theta_i) = L\Delta\theta (Equation 7.4.17).

Darcy's Law Application

• Expressed as q = -K \frac{\Delta h}{\Delta z} (Equation 7.4.18).

• q = -f because q is positive upward and f is positive downward.

Boundary Conditions

• Point 1 at the surface: h1 = h0.

• Point 2 at the wetting front: h_2 = -\psi - L.

• Darcy's law: f = K \frac{h_0 - (-\psi - L)}{L} (Equation 7.4.20a).

• Assuming h_0 is negligible: f = K \frac{\psi + L}{L} (Equation 7.4.20b).

Wetting Front Depth

• From Equation 7.4.17: L = \frac{F}{\Delta\theta}.

• Substituting into Equation 7.4.20: f = K \frac{\psi \Delta\theta + F}{F} (Equation 7.4.21).

Differential Equation

• Since f = \frac{dF}{dt}, Equation 7.4.21 becomes: \frac{dF}{dt} = K \frac{\psi \Delta\theta + F}{F}.

Solving for F

• \frac{F}{\psi \Delta\theta + F} dF = K dt.

• \int \frac{F + \psi \Delta\theta - \psi \Delta\theta}{\psi \Delta\theta + F} dF = \int K dt.

• F(t) - \psi \Delta\theta { \ln[F(t) + \psi \Delta\theta] - \ln(\psi \Delta\theta) } = Kt (Equation 7.4.22a).

• F(t) - \psi \Delta\theta \ln \left( 1 + \frac{F(t)}{\psi \Delta\theta} \right) = Kt (Equation 7.4.22b).

Green-Ampt Equation

• Equation 7.4.22: Cumulative infiltration.

• Infiltration rate: f = K \left[ \frac{\psi \Delta\theta}{F(t)} + 1 \right] (Equation 7.4.23).

• If h0 is not negligible, substitute \psi + h0 for \psi in Equations 7.4.22 and 7.4.23.

Successive Substitution

• Rearranging Equation 7.4.22: F(t) = Kt + \psi \Delta\theta \ln \left( 1 + \frac{F(t)}{\psi \Delta\theta} \right) (Equation 7.4.24).

Green-Ampt Parameters

• n: Porosity

• \theta_e: Effective porosity

• \psi: Wetting front soil suction head (cm)

• K: Hydraulic conductivity (cm/h)

• \Delta\theta = (1 - S_e)n.

• S_e: Effective saturation

• \Delta\theta in terms of initial saturation Si: \Delta\theta = n - \thetai = (1 - S_i)n (Equation 7.4.26).

Sample Problem: Green-Ampt Method

• Silty clay soil.

• Time increments: 0.1 hr up to 6 hr.

• Initial effective saturation: 20%.

• Continuous ponding.

Ponding Time

• Elapsed time between rainfall start and ponding.

• Using Green-Ampt equation with constant rainfall intensity i.

• Substituting F = it_p into Equation 7.4.23: i = K \left( \frac{\psi \Delta\theta}{F} + 1 \right).

• Solving for tp: tp = \frac{K \psi \Delta\theta}{i(i - K)}.

Other Infiltration Methods

Ф-index Method

• Constant abstraction rate.

Horton's Equation

• Empirical relation: f = fc + (f0 - f_c)e^{-kt} (Equation 7.4.28).

• Cumulative infiltration: Ft = fc t + \frac{(f0 - fc)}{k} (1 - e^{-kt}) (Equation 7.4.29).

Richard's Equation

• Solved by Philip (1957, 1969).

• Cumulative infiltration: F = St^{1/2} + Kt (Equation 7.4.30).

• Infiltration rate: f(t) = \frac{1}{2}St^{-1/2} (Equation 7.4.31).

• S: Sorptivity.

• As t \to \infty, f(t) \to K.

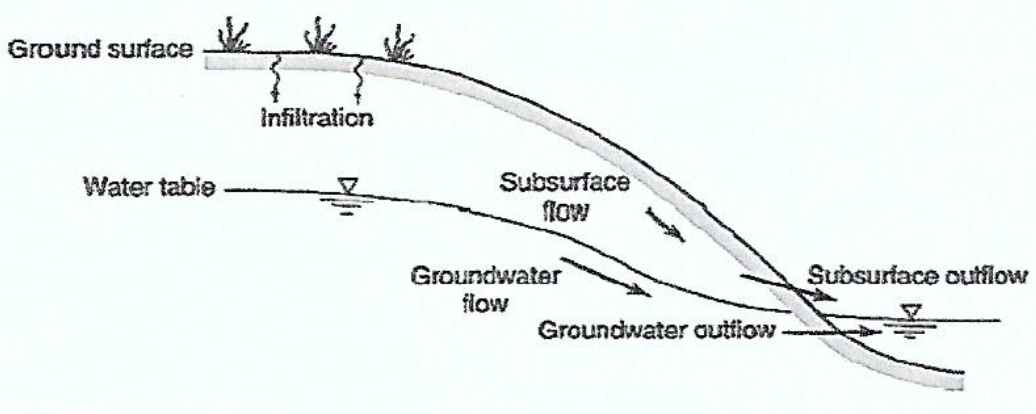
SUBSURFACE FLOW

Groundwater

• Rocks below a certain depth are saturated.

• Water flows towards lower elevation at equal pressure.

• Water flows towards lower pressure at equal elevation.

• Flow varies with material; larger holes mean faster flow.

Advantages of Groundwater

• Less seasonal variation than surface water.

• High biological purity due to slow movement.

• Constant temperature.

• Available virtually everywhere if deep enough.

Groundwater Properties

• All water beneath the surface.

• Occupies pores.

• Porous media contains numerous small pores.

• Pores contain fluids (water and air).

• Pores act as fluid conduits.

• Rock types and pore arrangement affect storage and flow.

Important Processes

• Infiltration creates soil moisture.

• Subsurface flow through soil.

• Groundwater flow.

Soil Zones

• Zone of aeration: Pores contain water & air.

  • Soil water zone: Water moves down (up) during infiltration (evaporation).

  • Vadose zone: Water held by capillary forces; near field capacity.

  • Capillary zone: Saturated at base, near field capacity at top; water pulled up from the water table.

Energy of Water in Soil

• Cohesion: Water molecules attract each other.

• Adhesion: Attraction between soil particles and water.

• Meniscus: Curved air-water interface as water drains.

• Determined by:

  • Pressure potential.

  • Gravity potential.

  • Osmotic potential: Water moves from low to high solute concentration.

Factors Affecting Water Movement

• Soil texture (particle size).

• Pore space.

• Soil moisture content.

• Slope of soil/rock layer.

Rates of Flow

• Typical groundwater flow: 0.01 m/yr to 100 m/yr.

• Permeability varies greatly; clean sandstone may have K = 0.1 m/s, while clay can have K = 1E-10 m/s.

Aquifers and Aquitards

• Aquifer: Yields sufficient water.

• Aquitard: Does not yield enough water.

• Unconfined aquifer.

• Confined aquifer.

Water Table

• Intersects the land surface at lakes, ponds, and streams.

• Streams can gain water from or lose water to the groundwater system.

• Water table is closest to the surface at streams.

• Perched water table.

Groundwater Use

• Drawdown: Depression of piezometric surface due to pumping.

• Cone of depression: Lowering of piezometric surface around a well.

• Shape depends on hydraulic conductivity, storativity, and layer thickness.

Geologic Action by Groundwater

• Weathering and cementation.

• Karst: Erosion by groundwater, forms caves and sinkholes that collapses.

Types of Aquifers

• Aquifer: Stores and transmits water.

  • Unconsolidated deposits: sand and gravel, sandstones etc.

• Aquiclude: impermeable boundaries of aquifers; stores, doesn't transmit.

  • Clays and less shale

• Aquitard: transmit don't store.

  • Shales and less clay

  • Leaky confining layers of aquifers

• Confined aquifer: Bounded by impervious layers.

• Unconfined aquifer:Bounded by a water table.

Groundwater Contamination

• Plumes: Created when contaminants enter the aquifer.

• Processes affecting plume movement:

  • Advection

  • Dispersion

  • Retardation

  • Chemical precipitation

  • Biotransformation

Plume Movement Processes

• Advection: water carries substance

• Dispersion: Spreading caused by advection

• Retardation: Contaminants held to aquifer solids temporarily

• Chemical Precipitation: heavy metals react with soils to precipitate in solid form.

• Biotransformation: Chemicals change form or are destroyed

RUNOFF AND STREAMFLOW

Surface Runoff

• Water that travels over the ground surface to a channel.

Peak Runoff Estimation by Rational Method

• Q_p = CIA

  • C is runoff coefficient, i is rainfall intensity (m/s), A is watershed area (m²) and Q_p is peak runoff (cms)

• Important for sizing storm water conveyance structures.

Limitations of Rational Method

• Runoff coefficient isn't dependent Rainfall rate and antecedent moisture conditions

• Rainfall is not uniform over the catchment area; Limit application to areas smaller than 80 has. (ASCE)

• Higher coefficients should be used for less frequent storms as smaller percentage of rainfall abstraction

Streamflow

• Measure of water volume transported by a stream.

Stream Parameters

• A stream begins at its headwaters, often in the mountains, fed by an underground spring or the runoff from rain and snow melt

• Measured by determining the cubic feet per second or gallons per hour.

Factors Influencing Flow Velocity

• Depth of stream channel

• Width of stream channel

• Roughness of stream bottom

• Slope or incline of surrounding terrain

Factors Influencing Stream Volume

• Weather or climate

• Seasonal changes

• Merging tributaries

• Human impact

Measurement

• Discharge: volume of water that flows past a point during a specific time, Usually reported as the number of cubic feet of water passing a point each second (cfs)

• Stillings wells are used to measure a streamflow

Watershed

• Area of draining to a stream

• Streamflow generated by water entering surface channels

• Affected by Physical, vegetative, and climatic features and Geologic considerations

• Annual Hydrographs and Storm Hydrographs

Baseflow Separation Techniques

• Straight line method

• Fixed base method

• Variable slope method

DIRECT RUNOFF AND EXCESS RAINFALL

• Excess (effective) rainfall

• Rainfall that is not retained or infiltrated

• Becomes direct runoff

• Excess rainfall hyetograph(excess rainfall vs time)

Abstraction (losses)

• Phi Index

• Difference between total and excess rainfall hyetographs

• Constant rate of abstraction yielding excess rainfall hyetograph with depth equal to depth of direct runoff

• a = \sum{m=1}^{M} (Rm - A_t)

Water Runoff Coefficients

• Ratio of the peak rate of direct runoff to the average intensity of rainfall in a storm

• Ratio of runoff to rainfall over a given time period

• \frac{\sum Rd}{\sum Rm}