Macromolecules- Large molecules built up by small molecules (monomers), that are covalently linked

Examples:

Biological polymers:

• Polysaccharides such as starch, cellulose etc.
  • Sugar monomers
• Lignin
  • Phenolic monomers

Proteins: Not strictly polymers

• Amino acid monomers

Synthetic polymers:

• Polyethylene (PE)
• Polyethylene glycol (PEG)
• Polyvinylalcohol (PVA)
• Polystyrene (PS)
• Polyacrylamide etc.

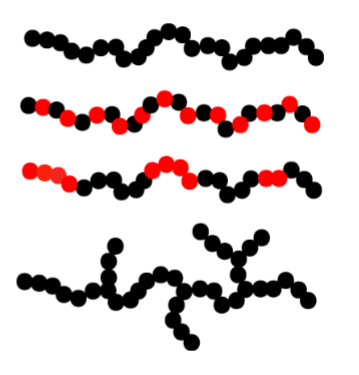
Homopolymer- same type of monomer

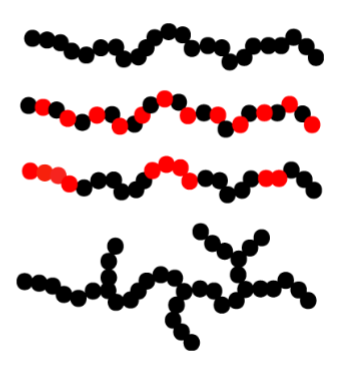
Copolymer- alternating monomer

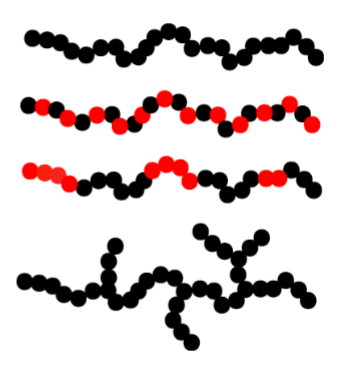
Block copolymer- alternating in block→ making them surface-active

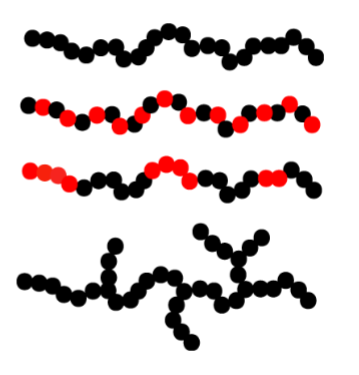
Branched homopolymer- branching can occur for others

Average molecular weight

• Molecular weight (molar mass) is given by:

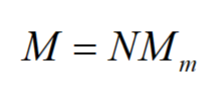
• Biopolymers and most synthetic polymers are polydisperse (different chain length).

– Average molar mass (molecular weight).

– Average molar mass depends on the method used to determine it.

Polymer size - Hydrodynamic radius

Hydrodynamic radius is obtained from the Stokes-Einstein equation. It describes how diffusion of a particle or polymeric structure depends on its radius.

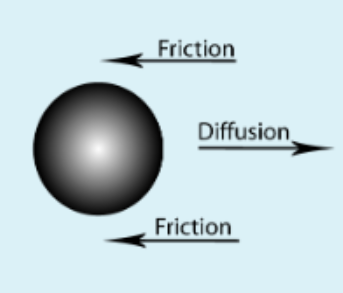
Stokes-Einstein

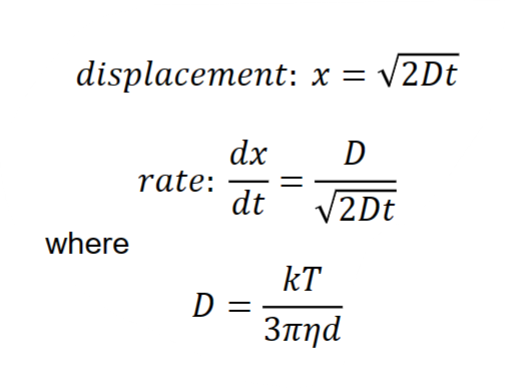
D= diffusion coefficient [m²/s]

k= Boltzmann constant (J/K)=1.38×10⁻²³ J/K

T= temperature (K)

η=dynamic viscosity of continuous phase [Pa•s]

d=hydrodynamic diameter of particle [m]

Polymer size - Radius of gyration

Based on the distance of each monomer unit to the polymer’s center of mass. Used for random coil polymer

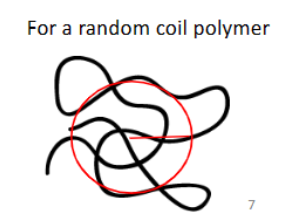
Debey’s definition of radius of gyration- It is most common one. Distance of every mass to the center of mass. The average distance is r_g

r_g=average distance

M_i=molar mass

r_i=distance to the center of mass

Polymer conformation in dilute solutions

Conformation in solutions depends on:

• Interactions with solvent molecules
• pH
• Salt
• Temperature
• Interactions with other polymer molecules

Really likes solvent: polymer swell

Doesn’t like it as much: polymer minimise

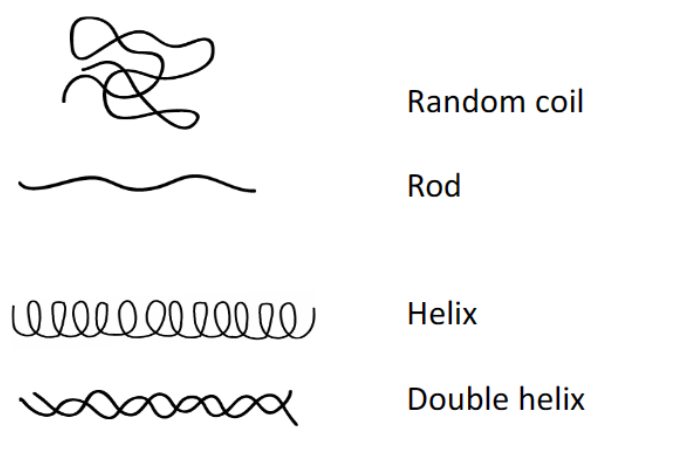
Conformation in dilute solutions

Rod: stiff

Double helix: two molecules

Flory-Huggins theory- Describes solubility of a polymer and thermodynamics of macromolecular solutions.

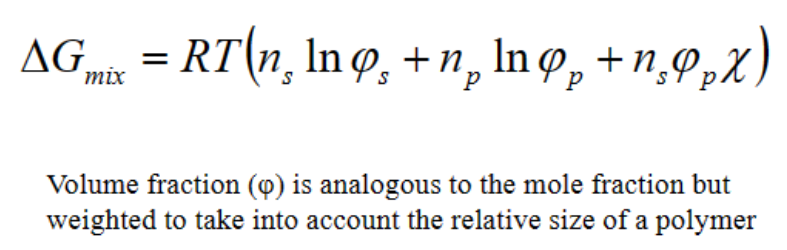
Volume fraction (φ) is analogous to the mole fraction but weighted to take into account the relative size of a polymer

The last sum: interaction between polymer and solvent

• The Flory-Huggins parameter (χ)

– 0.1< χ<0.5 ”Good” solvent (molecule swell)

– χ ≈ 0.5 ”θ-solvent” (transition between good and poor solvents) (reduce it bellow to precipitate, increase to allow it dissolve)

– χ > 0.5 ”Poor” solvent (molecule shrink)

– χ >> 0.5 Insoluble

• χ can change with temperature, pH, ionic strength etc.

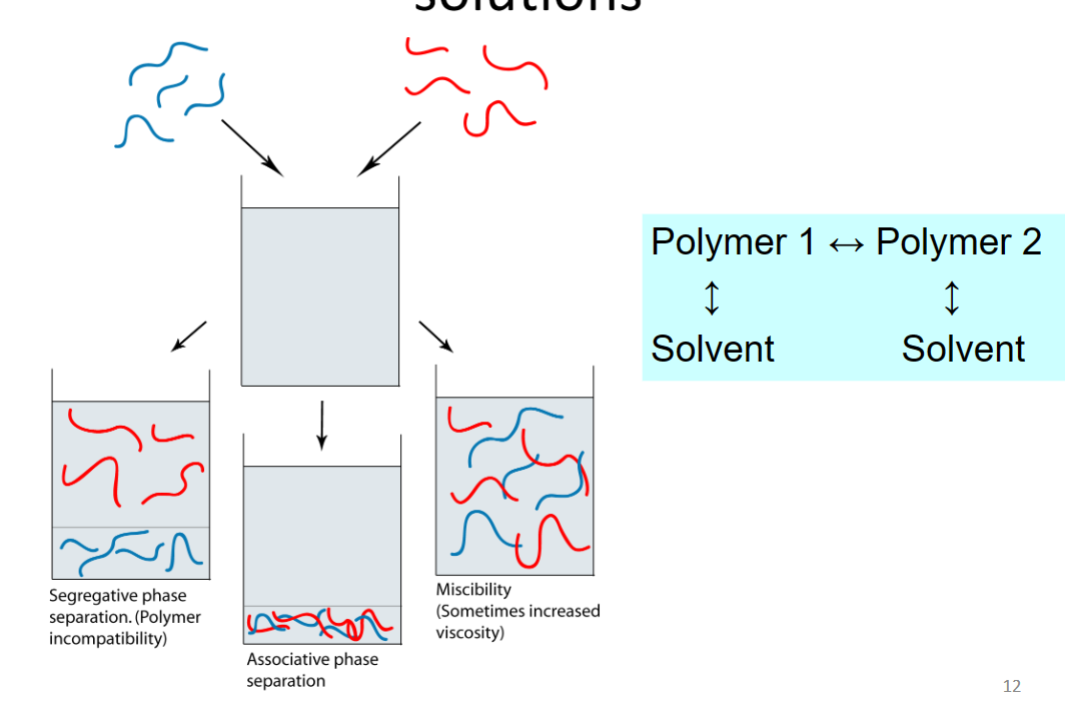
Phase behaviour of macromolecule solutions

Polymer 1 and polymer 2 are chemically different

Miscibility: polymers like the solvent, don’t care about each other

Segregative phase separation: Polymers don’t like each other but like solvent

• The rule for mixtures of non-ionic polymers

Associated phase separation: Polymers like each other better than solvents (e.g polymer could have opposite charges)

• Polyelectrolytes of opposite charge, proteins-polysaccharides

Phase behaviour of macromolecule solutions

• Cooling and heating can cause phase separation.

• θ-temperature.

• Example of phase diagram - Polyethylenoxide

Horizontal axis is concentration

The highest molecular weight is most sensitive high temperature

Interactions between water molecules decreases at that temperature, molecules becomes soluble again

Surface active macromolecules

• Proteins and polymers can be surface active
• Hydrophobic domains are excluded from a polar phase
• Hydrophilic domains ensure the solubility of the molecule
• May associate and form aggregates in the solution

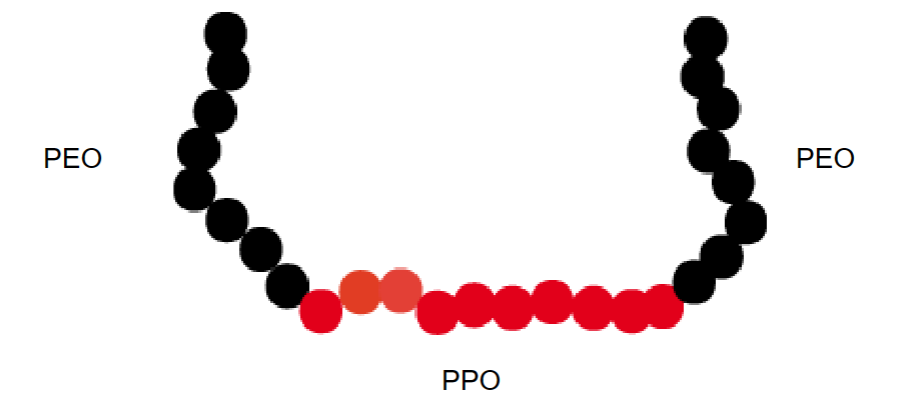
Example: Block co-polymers (Pluronic).

PEO=hydrophilic

PPO=hydrophobic

Applications of macromolecules

• Thickening to increasing viscosity to preferred value and flow properties in liquid formulations. Example: Pharmaceutics, Foods and Paints and coatings

• Stabilization of dispersions

Rheology - Rheology is the study of the flow and deformation of matter, including liquids, solids, and soft materials, under applied forces or stresses.

Shear stress- Shear stress is the external force applied parallel to the surface, which causes deformation.

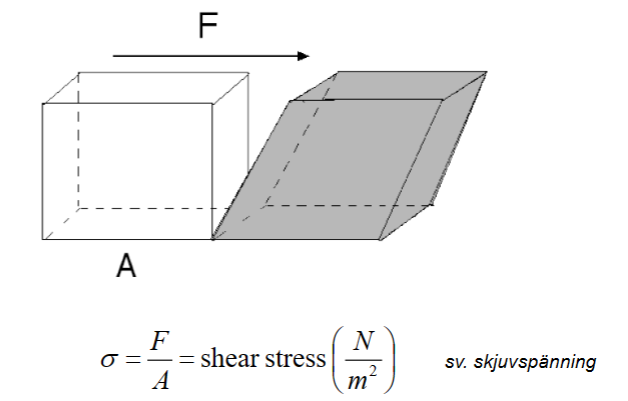
σ=shear stress [Pa]

F=applied external force [N]

A=cross-sectional area [m²]

Shear rate- Shear rate 𝛾 is the rate at which strain changes over time, which is the rate of deformation.

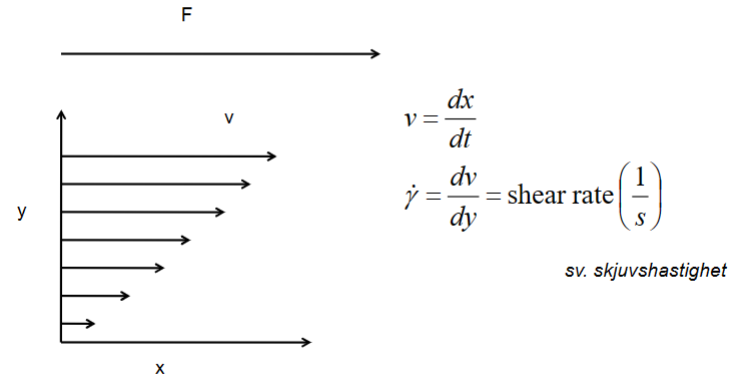
γ=shear rate [1/s]

v=velocity [m/s]

y=distance between moving plates [m]

Viscosity

In a pure liquid: friction between molecules

In a solution of polymers: resistance to a deforming flow compared to pure solvent → increase in viscosity

Normally for polymer: Shear-thinning behaviour arises from orientation of polymer chains

Dynamic viscosity-

γ=shear rate [1/s]

σ=shear stress [Pa]

η=dynamic viscosity [Pa・s=N・s/m²]

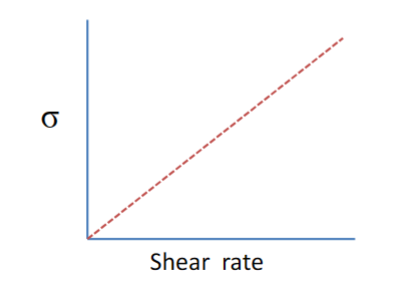
Newtonian flow

• Shear stress proportional to shear rate → viscosity independent of shear rate.

• Low molar mass liquids (water, organic solvent etc.).

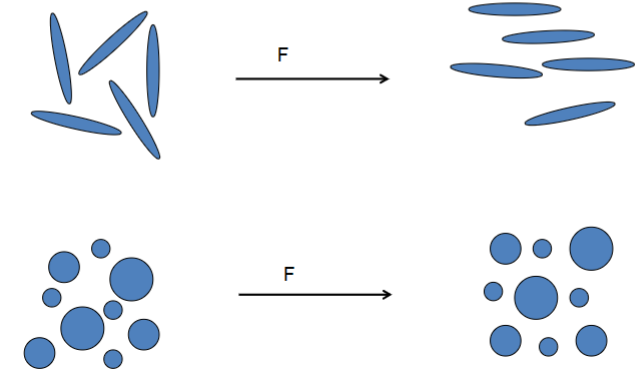
Viscosity increase in dispersions arises from disturbances in the flow field

Orientation of particles in the flow

What happens to the viscosity? The particles align themselves with the flow

Non-Newtonian flow

• The viscosity is shear rate dependant.

• Pseudo-plastic flow: The viscosity decreases with increasing shear rate (as known as shear-thinning). For example paint

• Dilatent flow: The viscosity increases with increasing shear rate. For example wet sand (particle volume fraction increase locally)

• Apparent viscosity

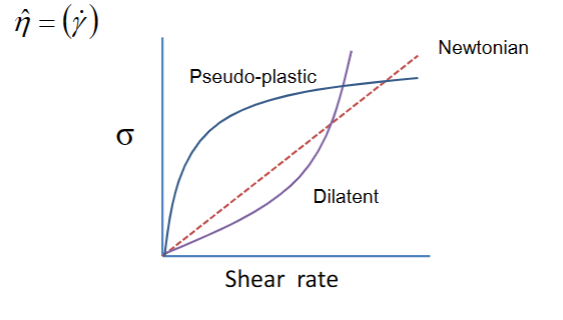
Non-newtonian behaviour arises from disturbances in the flow pattern caused by sample components

• The power law can be used to describe non-newtonian flow

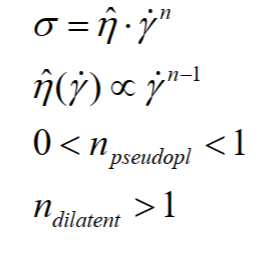
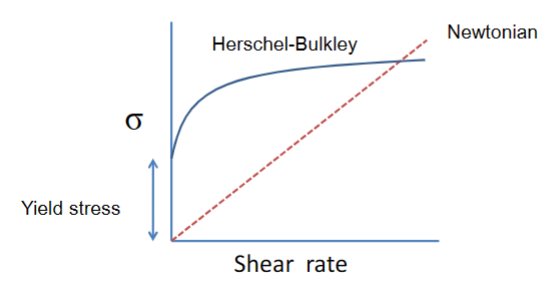
Yield stress

• Above the yield stress the system starts to flow.

• Below the yield stress the system appears solid (i.e. gel)

Herschel-Bulkley: Tooth paste, tomate ketchup

Viscosity of macromolecule solutions

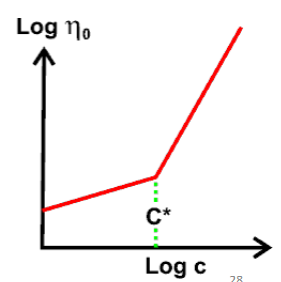
• The overlap concentration (c*) is the point where solution viscosity increases sharply

with polymer concentration

• c* depends on the volume occupied by polymer in the solution.

– Large volume → lower c*

– Small volume → higher c*

• Note that the volume is 3D!

– i.e. rod-like conformation occupies a large volume

Viscosity of macromolecule solutions

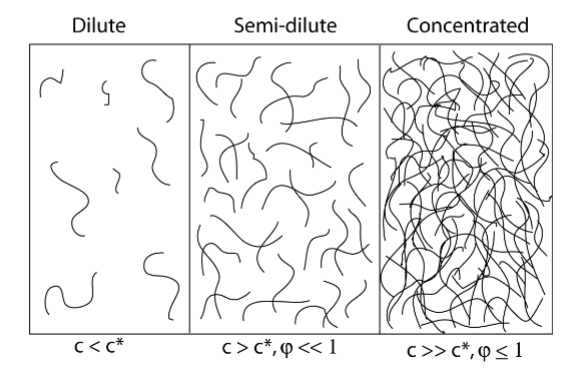
• Concentration regimes

Thixotropy- Thixotropic fluids are a type of non-Newtonian liquids that exhibit shear thinning during increased shear rate and a slow recovery to the original viscosity after the shear rate is removed.

• Time-dependent viscosity decrease during constant shear

• Obtained with associative thickeners – dissociation and orientation give a decrease in viscosity

• The viscosity is recovered when shearing/deformation stops

• Example: Important for controlling paint viscosity and application

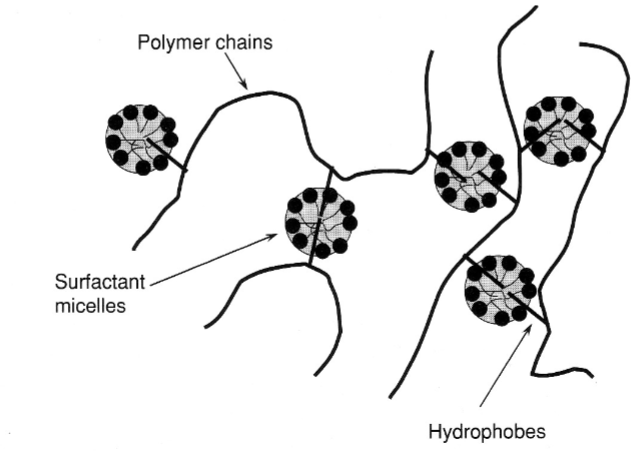
Associative thickeners

Hydrophobic interaction can play a role in polymer network formation

Surfactant micelles can associate with hydrophobic groups