7.2 Applications of the Normal Distribution


Learning Objectives

1. Find and interpret the area under a normal curve

2. Find the value of a normal random variable

Standardizing a Normal Random Variable

• Equation:

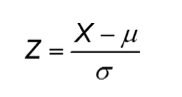
• What does this mean?

  • If a random variable X is normally distributed with a Mean μ and Standard Deviation σ, then the random variable is normally distributed with a Mean (μ) of 0 and a SD (σ) of 1. The random variable Z is said to have the standard normal distribution.

Standard Normal Curve

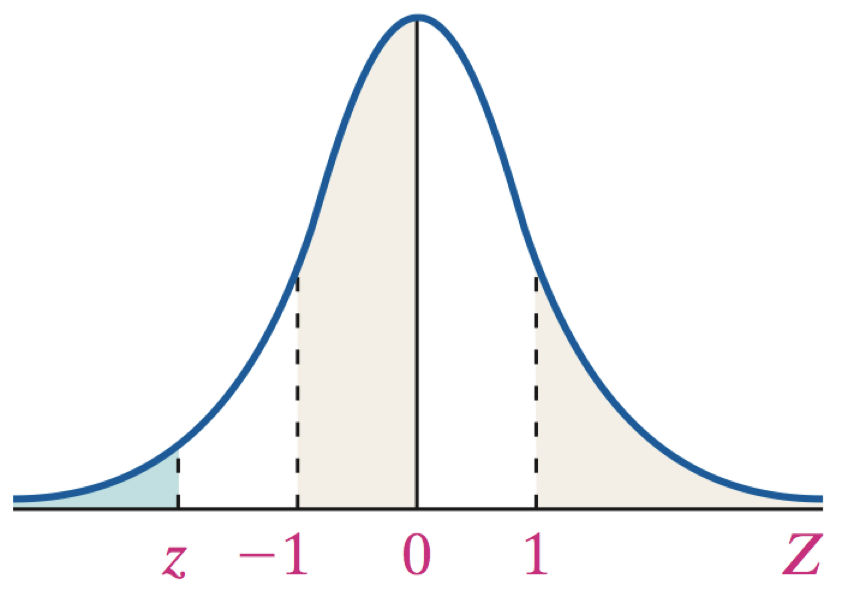
Area under the standard normal curve are values to the left of a specified Z-score, z, as shown in the figure.

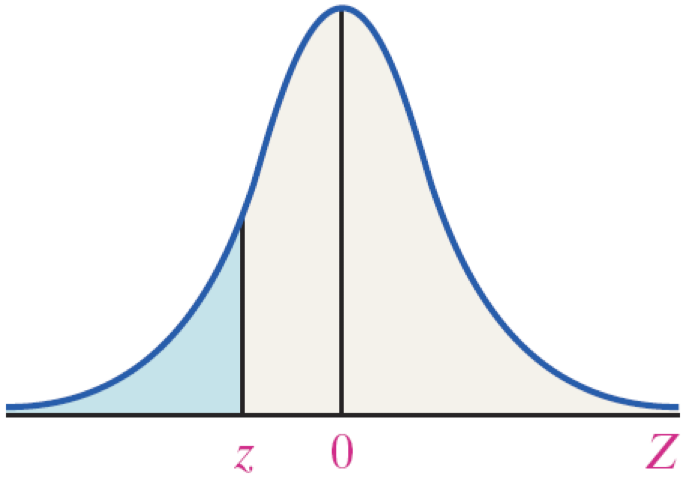
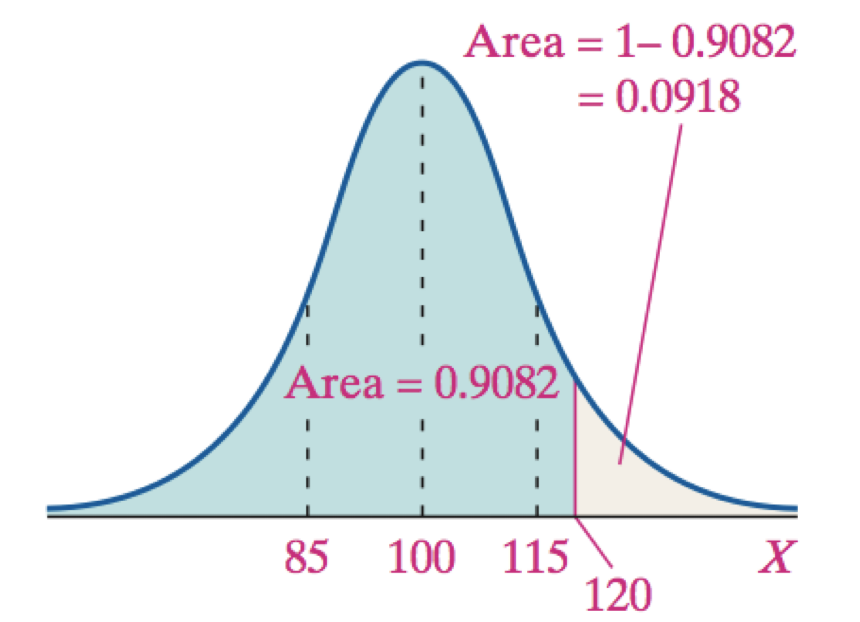
EXAMPLE IQ scores can be modeled by a normal distribution with μ = 100 and σ = 15.

How many standard deviations is an individual with an IQ score of 120 above the mean?

• 

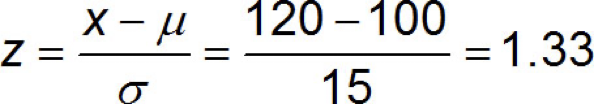
  • An individual whose IQ score is 120 is 1.33 SDs above the mean.

How do you find area under standard normal curve to the left of a z = 1.33

• You use this chart:

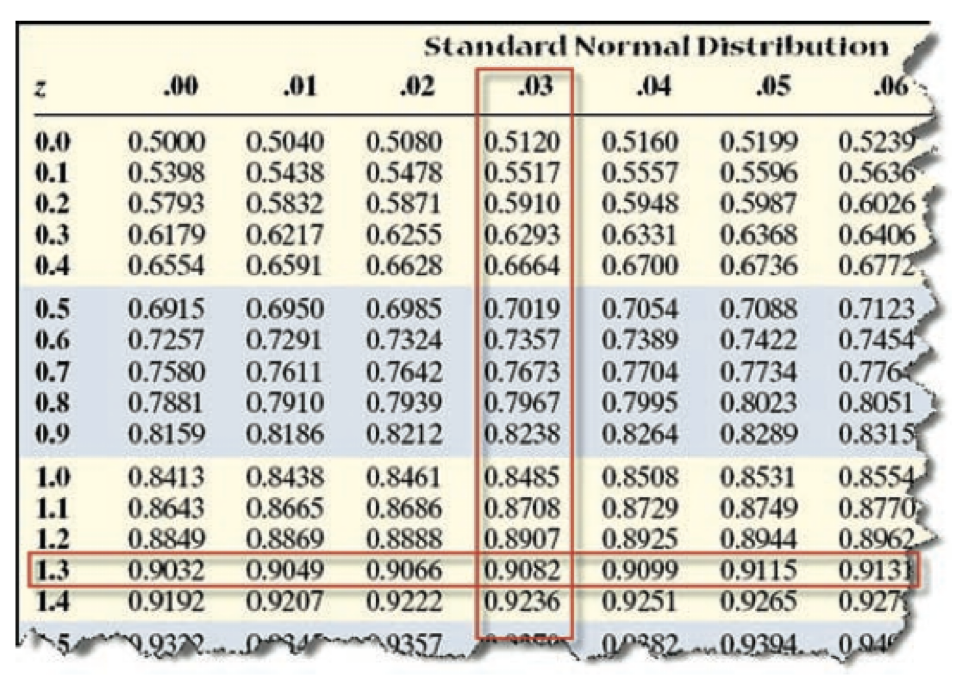
• The area under the standard normal curve to the left of z = 1.33 is 0.9082.

  • “the probability that a person has an IQ less than or equal to 120 is 90.82%”

    • alternative way to say: “the probability that a person with an IQ of 120 is at about the 91^st percentile.”

WARNINGS?? (IN GUIDED NOTES)

Use the Complement Rule to find the area to the right of z = 1.33.

Areas Under the Standard Normal Curve

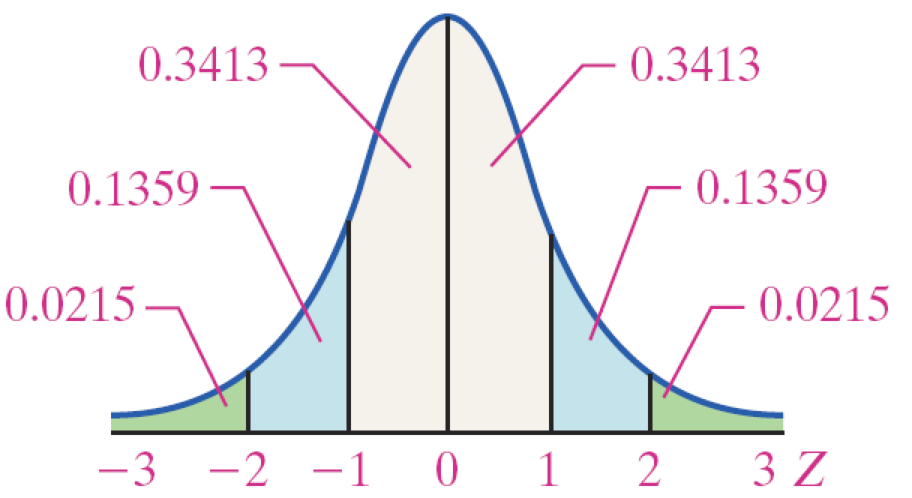
EXAMPLE Finding the Area Under the Standard Normal Curve to the Left of Z

(a) Find the area under the standard normal curve to the left of z = −0.38.

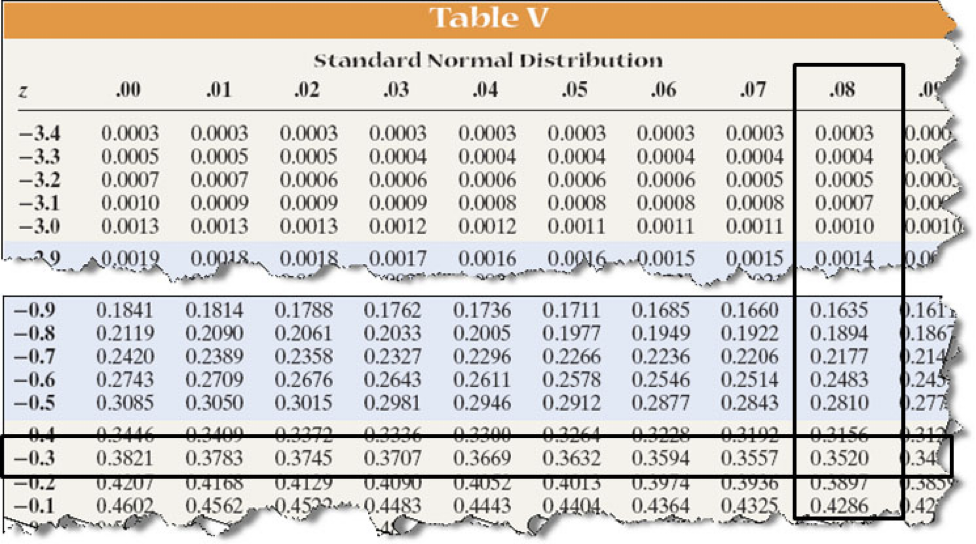
(a) area to left of a z = -0.38 is 0.3520

EXAMPLE Finding the Area Under the Standard Normal Curve to the Right of Z

(a) Find the area under the standard normal curve to the right of z = 1.25.

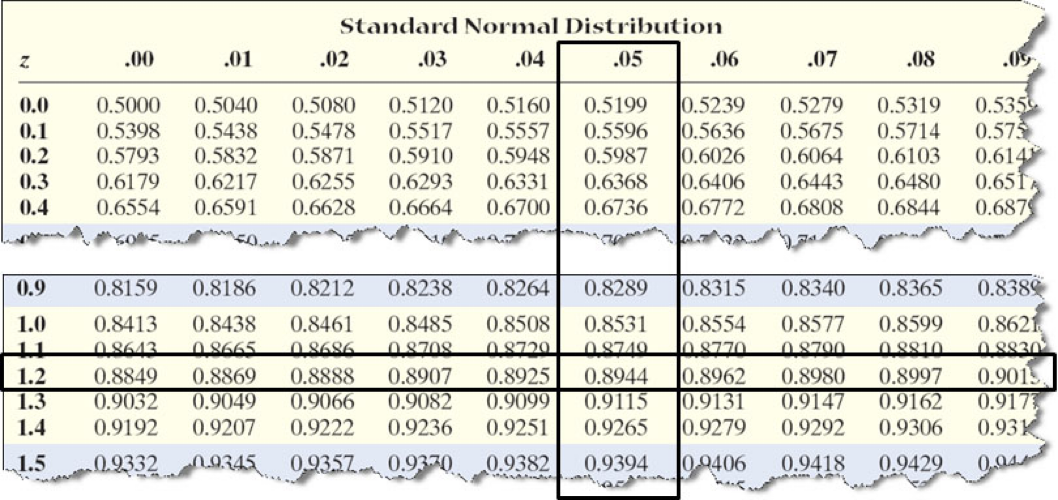
The area under the normal curve to the right of z is found by 1 − Area to the left of z_.

• 1 - area to left of 1.25

• 1 - 0.8944 = 0.1056

(a) Area to right of z = 1.25 is 0.1056

EXAMPLE Finding the Area Under the Standard Normal Curve

• Find the area under the standard normal curve between z = −1.02 and z = 2.94.

  • Area between −1.02 and 2.94 is equal to…

    • (Area left of z = 2.94) − (area left of z = −1.02)

• so that is 0.9984 − 0.1539 = 0.8445

Solution:

• Convert the value of x to a z-score (z= x-Mew/SD). Use Table V to find the row and column that correspond to z. The area to the left of x is the value where the row and column intersect.

• Use technology to find the area.

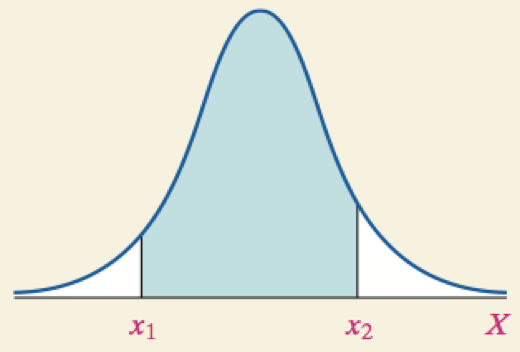
Solution:

• Convert the values of x to a z-scores. Use Table V to find the area to the left of z₁ and to the left of z₂. The area between z₁ and z₂ is (area to the left of z₂) − (area to the left of z₁).

• Use technology to find the area.

Using Minitab:

Graph > Probability Distribution Plot > View Probability

Default should be “Normal” Mean: 0.0 Standard Dev: 1.0

Options > a specified x value and select picture

Z-score(s) in X value blank

Click okay until picture comes up

Finding the Value of a Normal Random Variable 

Procedure for Finding the Value of a Normal Random Variable

Step 1: Draw a normal curve and shade the area corresponding to the proportion, probability, or percentile.

Step 2: Use Table V to find the z-score that corresponds to the shaded area.

Step 3: Obtain the normal value from the formula x = μ + zσ.

EXAMPLE 1 Finding the Value of a Normal Random Variable

The combined (verbal + quantitative reasoning) score on the GRE is normally distributed with mean 1049 and standard deviation 189. 

• What is the score of a student whose percentile rank is at the 85^th percentile?

  • The z-score that corresponds to the 85^th percentile is the z-score such that the area under the standard normal curve to the left is 0.85. This z-score is 1.04.

     x = µ + zσ

    x = 1049 + 1.04(189)

    x = 1246

    Interpretation: A person who scores 1246 on the GRE would rank in the 85^th percentile.

EXAMPLE 2 Finding the Value of a Normal Random Variable

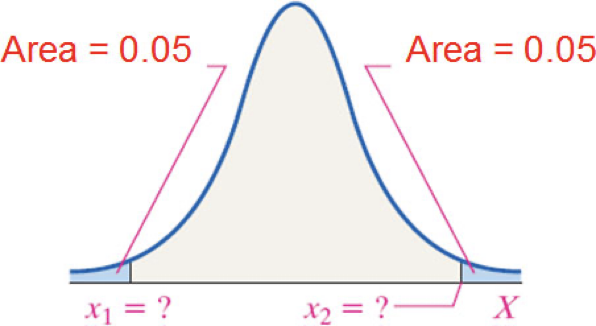
It is known that the length of a certain steel rod is normally distributed with a mean of 100 cm and a standard deviation of 0.45 cm. Suppose the manufacturer wants to accept 90% of all rods manufactured.

• Determine the length of rods that make up the middle 90% of all steel rods manufactured.

  • 

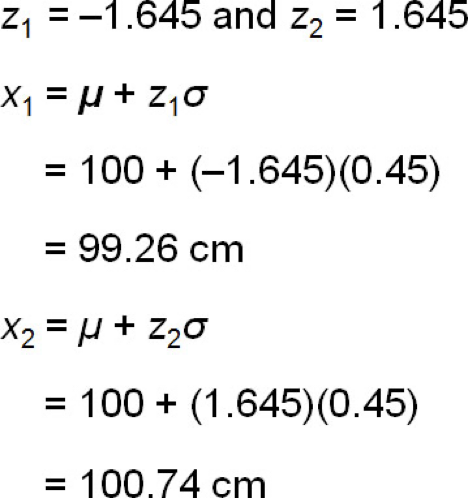
Interpretation: The length of steel rods that make up the middle 90% of all steel rods manufactured would have lengths between 99.26 cm and 100.74 cm.

The notation z_α

• (pronounced “z sub alpha”)

• is the z-score such that the area under the standard normal curve to the right of z_α is α.