Chapter 2 - Linear Relations and Functions

%%Vocabulary%%

==Special Notes==

^^Formulas^^

2.1 - Functions and Domain and Range

%%Domain:%% All possible x-values (input)

%%Range:%% All possible y-values (output)

%%Relation:%% The relationship between the inputs and outputs

%%Function:%% Each input only has one output

==Vertical Test:== to determine a function

^^Function Notation:^^ An equation represents a function can be written as f(x)

^^Standard Form:^^ Ax + Bx = C

^^Rate of Change = Slope^^

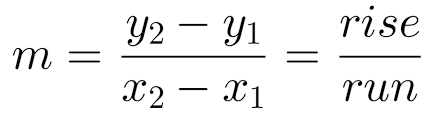Do not press delete

%%Parallel Lines:%% Same Slope

%%Perpendicular Lines:%% Slope 1 x slope 2 = -1 (reciprocal) Flip and opposite sign

%%Piece-defined Function:%% A function that is written in two or more expressions

==Closed dot = Include the point==

==Open dot = Do not include the point==

%%Parent Function (PF):%% The simplest function of each kind of function

==Constant Function:== @@PF: f(x) = a@@

==Identity Function (Linear Function):== @@PF: f(x) = x@@

==Absolute Value Function:== @@PF: f(x) = |x|@@

==Quadratic Function==: @@PF: f(x) = x^2@@

%%Transformations:%% Translation, flip over x or y axis, stretched or compressed.

%%Translations:%% Move up, down, left or right

==f(x) + k = up; f(x) - k = down; f(x + k) = left; f(x - k) = right==

%%Reflection%%:

%%Dilation%%: A dilation shrinks or enlarges a figure

%%Vertical:%%

==Compressed Vertically==	==Stretched Vertically==
a x f(x)	a x f(x)
0 < \|a\| < 1	\|a\| > 1

%%Linear Inequality%%: Resembles a linear equation but with an inequality sign

%%Boundary%%: A solid or dashed line that separates the shaded region and non-shaded region

==Sequence the steps for graphing a linear inequality:==