MVT, 1st & 2nd Deriv Test

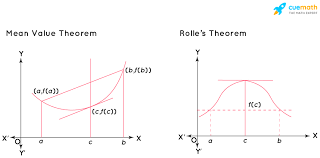
Mean Value Theorem:

• Conditions: f is continuous on [a,b] and differentiable on (a,b)

• MVT guarantees one value c on (a,b) where slope of tangent line = slope of secant line

  • f’(c) = (f(b)-f(a))/b-a *slope formula

• Rolle’s Theorem

  • if f(a)=f(b) then you can say there is a value c where f’(c)=0

Increasing or decreasing?

• if f’(x)>0 for (a,b), then f is increasing on [a,b]

• if f’(x)<0 for (a,b), then f is decreasing on [a,b]

• if f’(x)=0 for (a,b), then f is constant on [a,b]

1st Derivative Test

• if f’(x) changes from + to - at x=c, then (c,f(c)) is a relative max for f

• if f’(x) changes from - to + at x=c, then (c,f(c)) is a relative min for f

Concave up or down?

• if f’’(x)>0 for (a,b), then f is concave up on (a,b)

• if f’’(x)<0 for (a,b), then f is concave down on (a,b)

• Inflection points occur when:

  • f’’(x)=0 or undefined

  • f’’(x) changes signs (+ to - or - to +)

  • f’(x) changes from inc to dec or dec to inc

2nd Derivative Test

• if f’(c)=0 and f’’(x)>0 (concave up), then f has a local MIN at x=c

• if f’(c)=0 and f’’(x)<0 (concave down), then f has a local MAX at x=c