Rational Zero Theorem

Remainder Theorem

If a polynomial P(x) is divided by x-c, where c is a real number, then the remainder is P( c ).

• Finds the value of the remainder.

Factor Theorem

A polynomial P(x) has a factor x-c, where c is a real number, if and only if is P( c )=0

• Finds if the binomial is a factor of the polynomial.

Rational Theorem

Suppose that the polynomial function P(x)=XXXXXXX has integral coefficients.

If p/q is a rational zero of the polynomial function in lowest terms, where p is a factor of the constant coefficient and q is a factor of leading coefficient.

Factoring Polynomial

It is the inverse process of multiplying polynomials.

Descartes’ Rule of Signs

Rene Descartes

• 1596-1650

• French Mathematician

• To determine the number of real zeros of a polynomial function, Descartes’ Rule of Signs can be used.

Descartes’ Rule of Signs

Let P(x) be a polynomial function written in descending powers of x with real coefficients.

1. The number of positive real zeros of P(x) is either equal to the number of variations in sign in P(x), or is less than that number by a positive even integer.

2. The number of negative real zeros of P(x) is either equal to the number of variations in sign in P(-x), or it is less than that number by a positive even integer

A polynomial is said to have a variation in sign if two consecutive terms have opposite signs.

Upper and Lower Bound Theorem

Let P(x) be a polynomial with real coefficients and a positive leading coefficient. Suppose P(x) is divided by x-c using synthetic division.

1. If c>0 and each number in the third row is either positive or zero, then c is an upper bound for the real zeros of P(x).

2. If c<0 and the numbers in the third row are alternately nonpositive or zero and nonnegative, then c is a lower bound for the real zeroes of P(x)

Lower Bound has negative divisor = + - + - +

Upper Bound has positive divisor = + + + + +

Graphs of Polynomial Functions

Turning Point

• A turning point is a curve that is higher or lower than all points located nearby.

• This occurs when the function changes from sloping upwards to sloping downwards or vice versa.

Number of Turning Points

• The graph of a polynomial function of degree n has at most n-1 turning points.

If the symbols are “>” or “<“, used parenthesis () in the interval , in graphing used open circle.

• () - not included

If the symbols are “≥” or “≤”, used brackets in [] the interval, and graphing used shaded circles

• [] - included

If the symbols are “>” or “≥”, the solution set are the positive result from the product of signs.

If the symbols are “<“ or “≤”, the solution set are the negative result from the product signs.

Identifying the Graph

Even Degree & Positive Leading Coefficient

• The graph of a polynomial function comes down from the left and goes up to the right .

• If n is even and an>0.

  

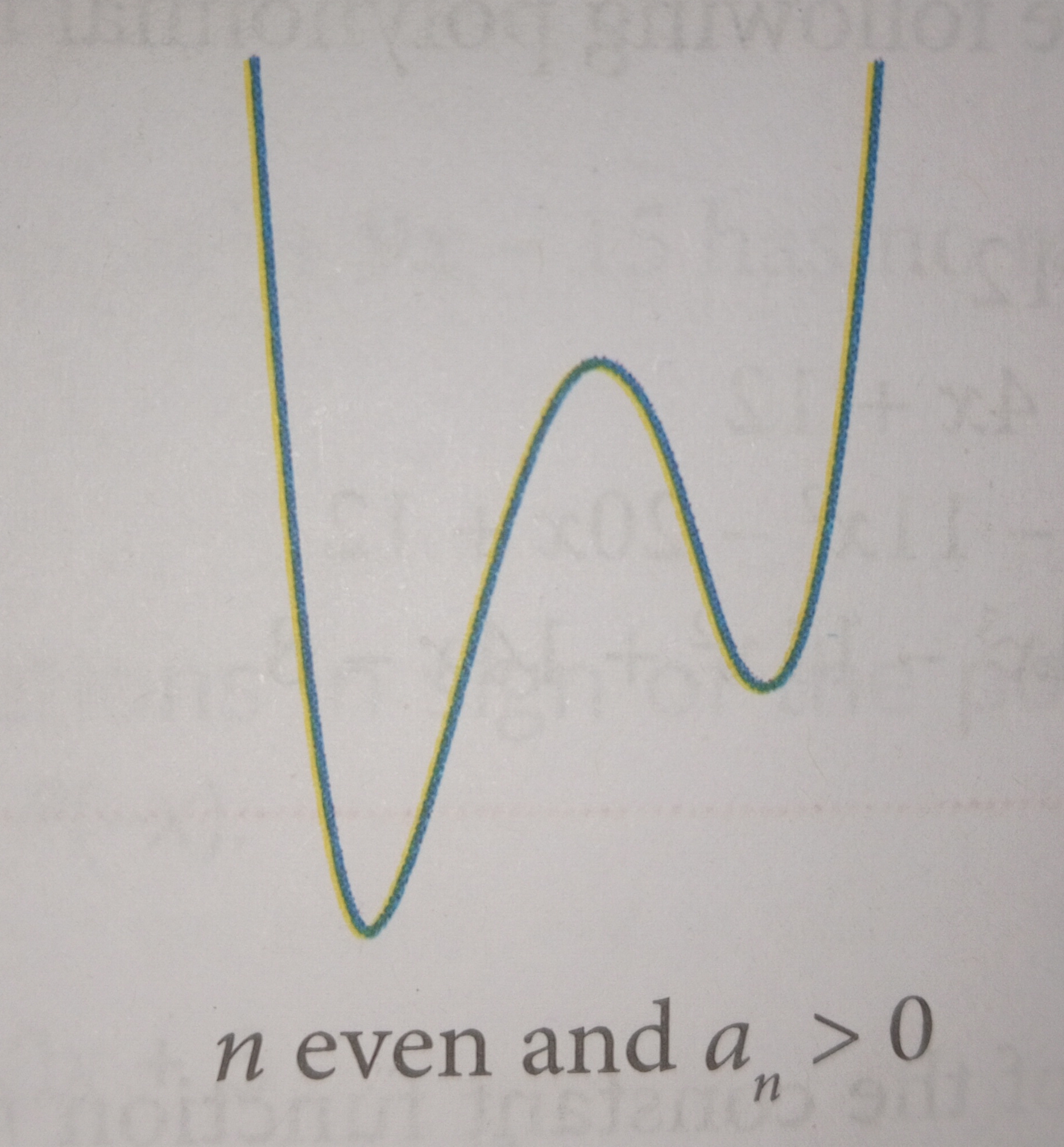
Odd Degree & Positive Leading Coefficient

• The graph of a polynomial function comes up from the left and goes up to the right.

• If n is odd and an>0.

  

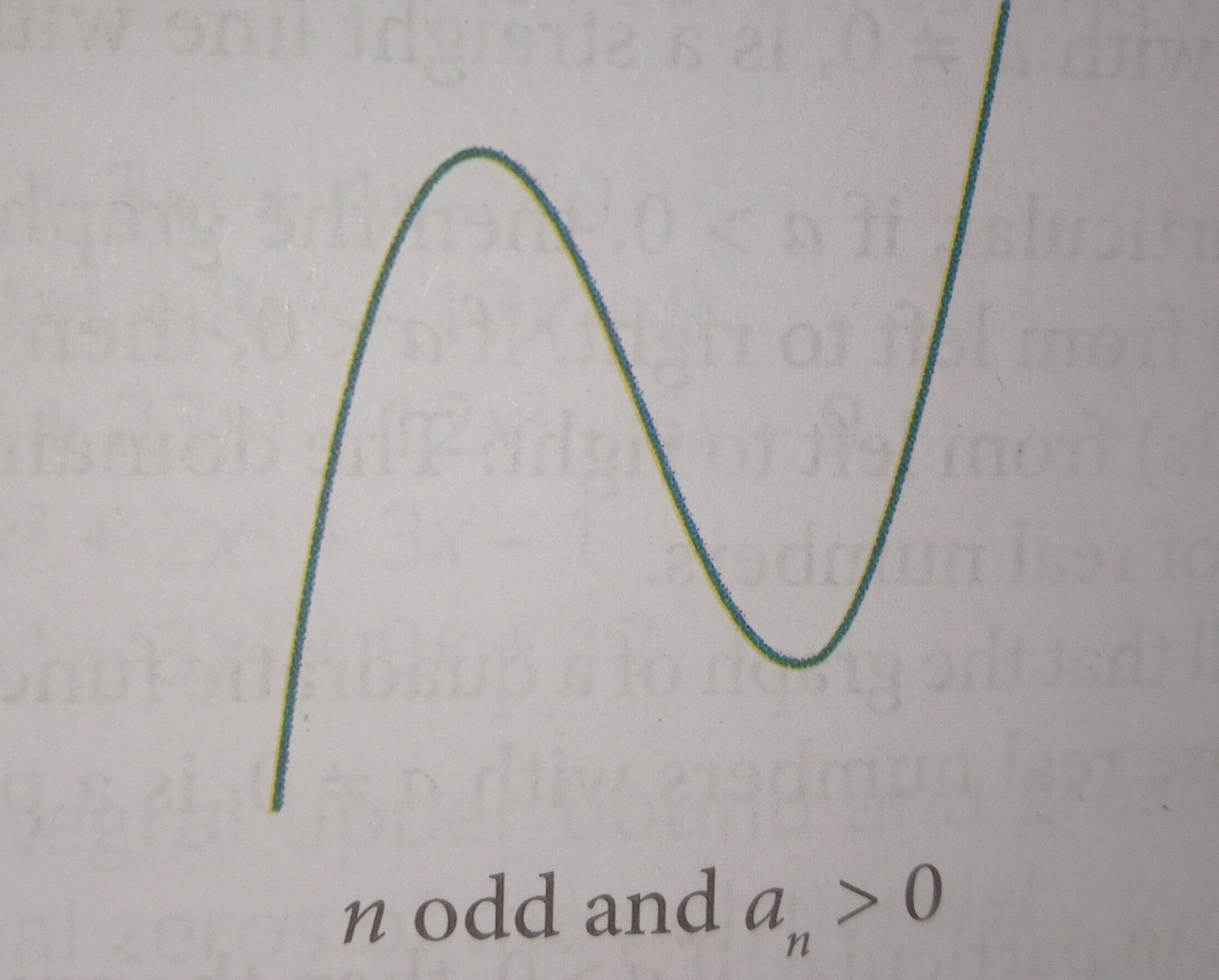
Even Degree & Negative Leading Coefficient

• The graph of a polynomial function comes up from the left and goes down to the right.

• If n is even and an<0.

  

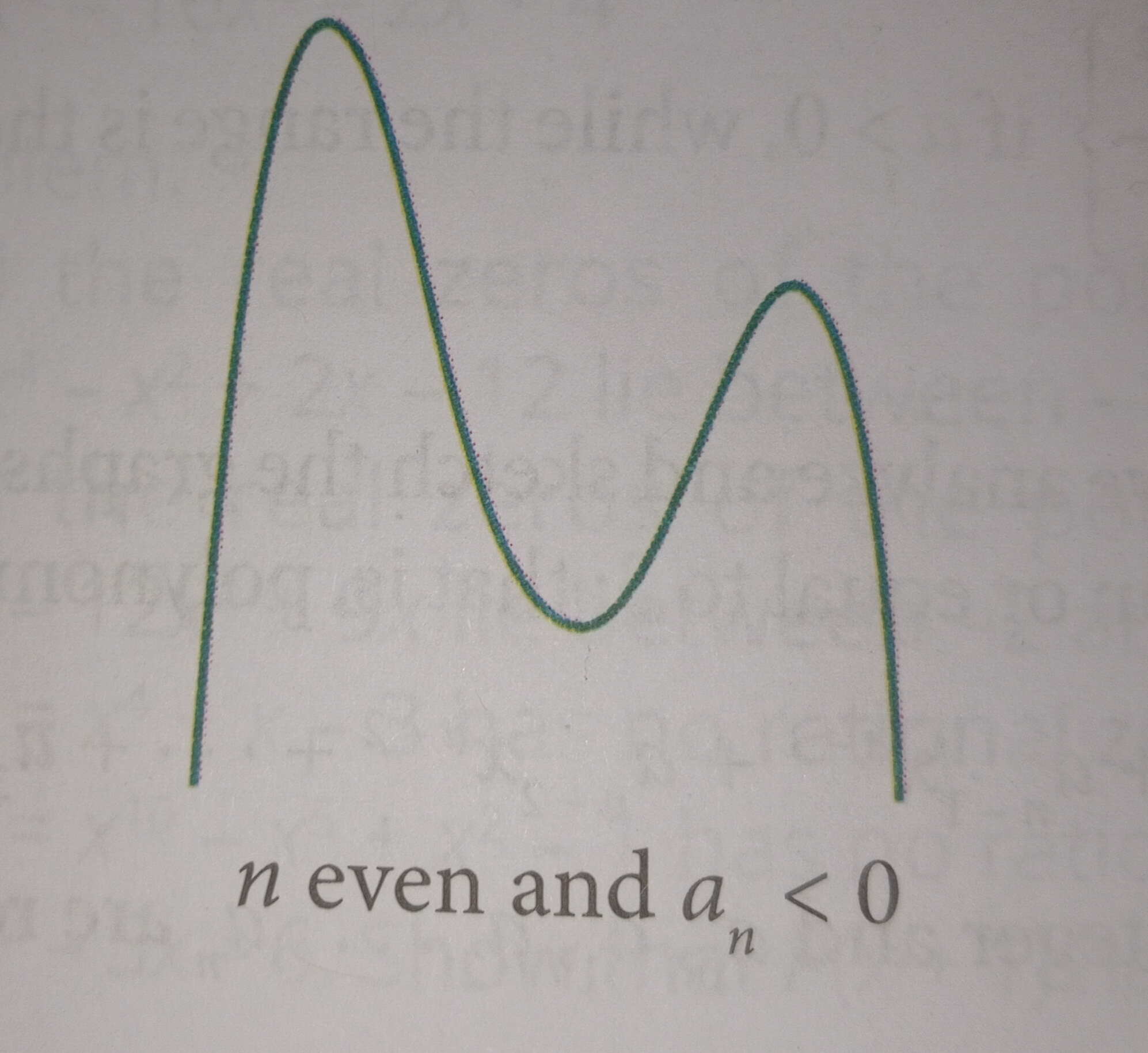
Odd Degree & Negative Leading Coefficient

• The graph of a polynomial function comes down from thee left and goes down to the right.

• If n is odd and an<0.

  

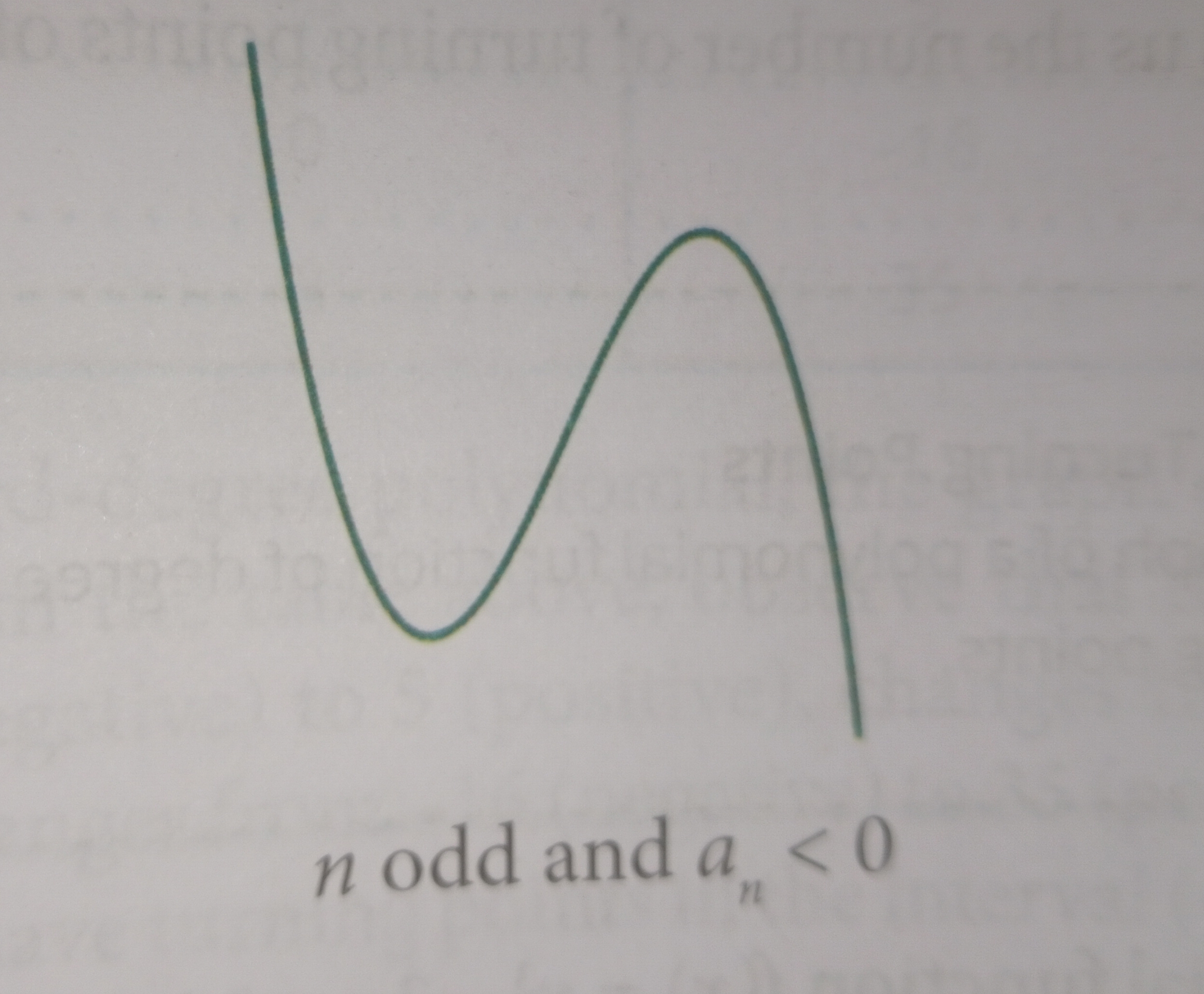
Circles and Related Terms Defined

Circle

• A circle is the set of all points having the same distance from a fixed point

• The fixed point is at the center

Radius

Radius is a segment having its endpoint the center and a point on the circle

Chord

Chord is a segment whose endpoints lie on the circle

Diameter

Diameter is a chord which passes through a center, and it is the longest chord, and its length is twice the radius

Angle

Central Angle

Central angle is an angle whose vertex is at the center of a circle

Arc

An arc is an unbroken part of a circle

An arc consists of all points on a circle between (and including) two giver points

An arc is denoted by the symbol “rainbow” placed above the endpoints that form the arc

Semicircle

Semicircle is an arc with measure 180 degrees whose endpoints are the endpoints of a diameter

A semicircle is named using three points

The Entire Circle

The entire circle is then the arc intercepted by one complete revolution

The entire circle’s measure is 360 degrees

Minor Arc

A minor arc is an arc which is smaller than a semicircle. ITs measure (and that of its central angle) is less than 180 degrees

A minor arc is named by using only two points, which are the two endpoints of the arc.

Major Arc

A major arc is an arc which is bigger than a semicircle. Its measure (and that of its central angle) is greater than 180 degrees

A major arc is named by using 3 points (sometimes by using only two points) in the same way that we name a semicircle

Arc Addition Postulate

Congruent circles are the circles with congruent radii

Congruent arcs are arc of a circle or of congruent circles that have equal measures

Theorem 3.1.1

In the same circle or two congruent circles, two arc are congruent if and only if their central angles are congruent

Theorem 3.1.2

In the same circle or two congruent circles, two minor arcs are congruent if and only if their chords are congruent

Theorem 3.1.3

A line through the center of a circle bisects a chord if and only if it is perpendicular to the chord

Theorem 3.1.4

In a circle, two chords are congruent if and only if they have the same distance from the center

Inscribed Angle and Intercepted Arc

Inscribed Angle

Inscribed angle is an angle whose vertex lies on the circle and whose sides are determined by two chords

Intercepted Arc

Intercepted arc is an arc that lies in the interior of an inscribed angle

Inscribed Angle Theorem

In a circle, an inscribed angle is half the measure of the central angle intercepting the same arc

Corollary 3.2.1

In a circle, an inscribed angle is half the measure of the intercepted arc

Corollary 3.2.2

In a circle, an inscribed angles intercepting the same arc are congruent

Corollary 3.2.3

An angle inscribe in a semicircle is a right triangle

Corollary 3.2.4

If a quadrilateral is inscribed in a circle, any two opposite angles are supplementary, angle inscribe in a semicircle is a right triangle