Chapter 3: Probability Topic

3.1 Terminology

• Experiment: is a planned operation carried out under the controlled condition

• Outcome: Result of an experiment

• Sample space: a set of all possible outcomes

• Event: any combination of outcomes that are usually represented by the letters A and B.

• Equally Likely: Each outcome of an experiment has the same probability.

• Probability: the chance of the outcome of an event

• “OR” Event: an outcome is in the event A OR B if the outcome is in A or is in B or is in both A and B.

• "AND" Event: an outcome is in the event A AND B if the outcome is in both A and B at the same time.

• Conditional probability: A given B is written P(A|B). P(A|B) is the probability that event A will occur given that event B has already occurred

• Complement: A given B is written P(A|B’)

  

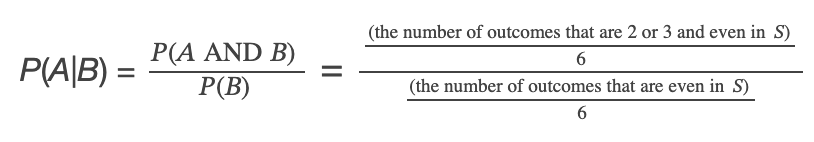
3.2 Independent and Mutually Exclusive Events

• Independent: One event occurring does not affect the chance that the other event occurs.
• Sampling with replacement: then events are considered to be independent, meaning the result of the first pick will not change the probabilities for the second pick.
• Sampling without replacement: the probabilities for the second pick are affected by the result of the first pick. The events are considered to be dependent or not independent.
• The events are independent if this is true:
  • P(A|B) = P(A)
  • P(B|A) = P(B)
  • P(A AND B) = P(A)P(B)
• Mutually exclusive: If events occur at the same time
  • P(A and B) = 0

3.3 Two Basic Rules of Probability

• Multiplication Rule: If A and B are two events defined on a sample space, then: P(A AND B) = P(B)P(A|B). A and B are independent, then P(A|B) = P(A). Then P(A AND B) = P(A|B)P(B) becomes P(A AND B) = P(A)P(B)
  • P(A|B) = 𝑃(𝐴 AND 𝐵) / 𝑃(𝐵)
• Addition Rule: If A and B are defined on a sample space, then: P(A OR B) = P(A) + P(B) - P(A AND B). If A and B are mutually exclusive, then P(A AND B) = 0. Then P(A OR B) = P(A) + P(B) - P(A AND B) becomes P(A OR B) = P(A) + P(B)

3.4 Contingency Tables

• Contingency table: provides a way of portraying data that can facilitate calculating probabilities.

3.5 Tree and Venn Diagrams

• Tree diagrams: used to determine the outcomes of an experiment. It consists of "branches" that are labeled with either frequencies or probabilities.
• Venn diagrams: a picture that represents the outcomes of an experiment. It generally consists of a box that represents the sample space S together with circles or ovals. The circles or ovals represent events.

\