Ch02 Hydrogen-like Atomic Orbitals — Quick Notes

Overview

• Hydrogen-like atomic orbitals described by the Schrödinger equation; energy levels depend on the principal quantum number n.

• Bohr model relation (precursor): discrete energy levels and discrete radii; spectral series names include Lyman, Balmer, Paschen, Pfund, etc.

• Energy for hydrogen-like levels:

  

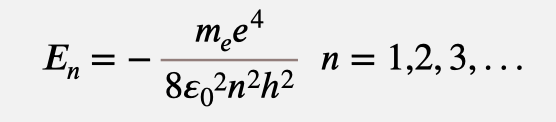
• Wavefunctions are indexed by quantum numbers $n, \ell, m$ (and spin $ms$): $\psi</em>{n\ell m m<em>s}(\mathbf{r}) = R</em>{n\ell}(r)\,Y<em>\ell^{m}(\theta,\phi)\,\chi</em>{m_s}$, with radial and angular parts.

Schrödinger Equation and Wave Functions

• The Schrödinger equation describes orbitals as spatial probability densities $|\psi|^2$ (always nonnegative).

• Solutions separate into radial part $R<em>{n\ell}(r)$ and angular part $Y</em>{\ell}^{m}(\theta,\phi)$ in spherical coordinates.

• Orbitals are labeled by four quantum numbers: $n, \ell, m, m_s$.

Quantum Numbers

• Principal quantum number: $n = 1,2,3,\ldots$ defines energy level.

• Angular momentum quantum number: $\ell = 0,1,2,\ldots,(n-1)$ defines orbital shape.

• Magnetic quantum number: $m = -\ell, -\ell+1, \ldots, +\ell$ defines orientation.

• Spin quantum number: $m_s = +\tfrac{1}{2}, -\tfrac{1}{2}$ (spin of electron; not an orbital quantum number).

• Degenerate set: for a given $n$, there are $n^2$ orbitals in total.

• For each $n$, there exists an $s$ orbital ($\ell=0$).

Orbital Types (by $\ell$)

• s orbital: $\ell=0,\; m=0$; 1s, 2s, 3s, …; spherical electron density.

• p orbitals: $\ell=1,\; m=-1,0,+1$; 2p, 3p, 4p, …; oriented along axes (px, py, pz).

• d orbitals: $\ell=2,\; m=-2,-1,0,+1,+2$; 3d, 4d, 5d, …; five distinct shapes.

• f orbitals: $\ell=3,\; m=-3,-2,-1,0,+1,+2,+3$; seven distinct shapes.

Node Structure and Radial Probability

• Radial nodes: $n_r = n - \ell - 1\,.$

• Total nodes: $\text{nodes} = n - 1$ for any orbital.

• For fixed $n$, increasing $\ell$ changes the radial distribution and angular nodal structure.

• Radial probability density (4πr^2|ψ|^2) shows where an electron is likely to be found on a sphere of radius r.

• Higher $n$ → larger average radius and more radial nodes.

• Nuclear penetration: density near the nucleus; s orbitals have greater near-nucleus density (penetration) than higher-ℓ orbitals.

Shapes, Orientation, and Key Concepts

• s: spherical symmetry; one orbital per $n$ (for each $n$ there is 1s, 2s, 3s, …).

• p: three lobes along axes; $m= -1,0,+1$ correspond to orientations along x, y, z (px, py, pz).

• d: five shapes; more complex angular distributions.

• f: seven shapes; even more complex.

• For each type, increasing $n$ enlarges the orbital and adds radial nodes (e.g., 2s, 3s, 4s; 2p, 3p, 4p; 3d, 4d, 5d).

• Energy ordering: within a given $n$, different $\ell$ states have different energies due to fine structure and penetration effects (conceptual; actual ordering depends on perturbations beyond the basic hydrogen model).

Quick Takeaways for Exam (Most Important Points)

• Quantum numbers: $n$, $\ell$, $m$, $ms$ with definitions above; orbitals are labeled $\psi</em>{n\ell m m<em>s}$ and can be written as $\psi</em>{n\ell m m<em>s}(\mathbf{r}) = R</em>{n\ell}(r)\,Y<em>\ell^{m}(\theta,\phi)\,\chi</em>{m_s}$.

• Energy levels depend only on $n$ in the hydrogenic model: $E<em>n = -\dfrac{R</em>H}{n^2}$.

• For each $n$: $\ell = 0,1,2,…,n-1$; number of orbitals total for that $n$ is $n^2$.

• Nodes: radial nodes $n_r = n - \ell - 1$; total nodes $n - 1$.

• Orbital shapes: s (spherical), p (two-lobed/dumbbell along axes), d (clover/other complex shapes), f (more complex shapes).

• Electron density is given by $|\psi|^2$; density near nucleus is called penetration, with s orbitals penetrating more than higher-$\ell$.

• For each $n$, there exists an s orbital ($\ell=0$); as $n$ increases, orbitals grow in size and acquire more radial nodes.