physics unit 10

Parts of the Atom

Matter is anything that has mass and takes up space. All matter is made of particles called atoms, the smallest units of an element that display the characteristic properties of that element.

Atoms have a very small, dense nucleus forming their central core made of positively charged protons and neutrally charged neutrons. They also have a much larger cloud of negatively charged electrons that orbit the nucleus.

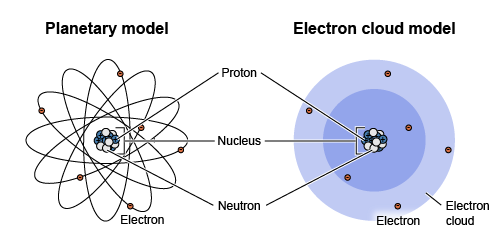
Note that while atoms are often drawn with the electrons orbiting like planets, as in the first image above, they actually exist in a cloud, as in the second image above.

• Protons are positive and in the nucleus

• Neutrons are neutral and in the nucleus

• Electrons are negative and in the cloud

In the ground state, the electrons in the atom are arranged so the atom has its lowest possible energy.

Atomic Models

Throughout history, scientists have tried to determine the shape and layout of an atom. It began when John Dalton theorized that atoms were spheres. Then J.J. Thompson created the Plum Pudding Theory where the atom was similar to plum pudding in that it was spherical, but the protons, neutrons and electrons were floating in the sphere like the fruits in the pudding. Then Rutherford identified the nucleus and the nuclear model was created. Niels Bohr modified Rutherford's theory to include fixed electron orbitals. This model is most commonly used for drawing atoms. The Quantum Model by Schrodinger is the accepted model by scientists today as electrons move in waves around the nucleus rather than fixed orbitals.

Protons and neutrons are made up of even smaller particles—quarks.

Protons and neutrons are composed of even smaller particles called quarks which are a type of fundamental particle called a fermion. Quarks interact through the strong nuclear force (which holds the nucleus together) and also carry electric charges. Although there are six types of quarks, we will only discuss two types here:

• Up quarks are particles with a +2/3 charge.

• Down quarks are particles with a −1/3 charge.

Protons are made of two up quarks and one down quark 

Neutrons are made of one up quark and two down quarks

Because protons and neutrons are made of quarks, each is a composite particle called a hadron.

What holds the nucleus together?

• First, neutrons create a buffer that separate the protons a little, reducing the repelling electric force between the protons.

• Second, a stronger attractive force inside the nucleus called the strong nuclear force provides an attractive force that holds the protons together.

Attraction between quarks makes up the strong force.

Attraction between quarks holds protons together. This force of attraction is called the strong nuclear force. The strong nuclear force is so strong that it actually goes beyond a single proton and pulls on quarks inside other protons, called residual strong interaction. The residual strong interaction holds the atomic nucleus together so powerfully because quarks in one proton pull on quarks in another proton, binding the protons firmly together.

The strong nuclear force is the strongest force in nature (approximately 100 times greater than electromagnetism and  times stronger than gravity). However, it acts over a short distance (about 1 femtometer or  m).

The weak nuclear force is responsible for radioactivity.

Physicists discern the atomic structure from the pieces left after a collision.

Scientists inject charged particles into a particle accelerator. The accelerator speeds the particles up to high energies and near relativistic speeds. The high-energy particles smash into the nuclei of target atoms. The high energy is required to overcome any forces within the nucleus.

The collision breaks apart the nucleus, producing new elements (with smaller nuclei), radiation, energy, and subatomic particles, all of which are detected with various types of detectors in the collision chamber.

Mass Number Calculations

An isotope is an atom with a different number of neutrons in the nucleus than other atoms of that same element.

There are three key components to atomic symbols of isotopes:

• The chemical symbol identifies the element.

• The mass number shows how many protons and neutrons are in the nucleus.

• The atomic number shows how many protons are in the nucleus.

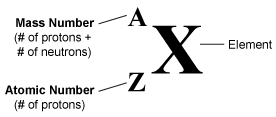
The number of protons shows which element is present. If you know the number of protons, you can identify the element using the periodic table.

However, the number of neutrons may differ, depending on the isotope of the element. By subtracting the atomic number from the mass number, you can find the number of neutrons.

mass number - atomic number = # of neutrons

Isotopes

All atoms have one or more isotopes, also known as radioisotopes. Isotopes are atoms with the same number of protons but different numbers of neutrons in the nucleus. Since neutrons have mass, two isotopes of the same element have different atomic masses. The atomic mass listed in the periodic table is the weighted average mass of the isotopes of that element.

Nuclear Chemistry - Isotope Stability

Stable isotopes have a nucleus that does not decay over time. Different elements have different numbers of stable isotopes. For example, tin (50 protons) has 10 stable isotopes, and carbon (6 protons) has 2 stable isotopes. Lead (82 protons) is the heaviest element with naturally occurring stable isotopes.

• Heavy stable isotopes have more neutrons than protons, 01​n>11​p

• Light stable isotopes have fewer neutrons than protons, 01​n<11​p

Unstable isotopes, or radioisotopes, have a nucleus that breaks down over time in the process of radioactive decay. In heavy elements, the electrostatic repulsion forces between positively charged protons are stronger than the strong nuclear forces (attractions) between protons and neutrons in the nucleus. Since the strong nuclear force acts only over very short distances, heavier elements are more likely to undergo radioactive decay.

Particle accelerators found antimatter.

More peculiar particles were also found to be released by atoms during radioactive decay and during collisions in particle accelerators. One particle, called a positron, has the same mass as an electron but a positive charge; because of its mass and charge, it is also called an antielectron. Physicists also found antiprotons (with the same mass as a proton, but a −1 charge). These antiparticles were combined in a particle accelerator at CERN in the mid-1990s to make an atom of antihydrogen. Atoms composed of positrons and antiprotons are called antimatter.

Uses for Radioactivity

Stable and unstable isotopes have applications across different fields, including but not limited to medicine, archeology, geology, and paleontology.

Carbon dating uses half-lives to determine the approximate age of fossils. Carbon-14 which is an unstable isotope of carbon has a half-life of about 5,000 years. When fossils are found, they compare the amount of Carbon-14 in the fossil to the amount of Carbon-14 in a living tissue. If the fossil has 100 carbon-14 nuclei and the living tissue has 400 carbon-14 nuclei, they can determine the fossil is about 10,000 years old. (200 nuclei would mean 5,000 years old as this is half of 400. 100 is half of 200 so it has gone through the process twice meaning 10,000 years).

There is a common misconception that carbon dating is used to date rocks, but this method can only be used for living organisms. The living organisms take in carbon and use it so the body retains what is left after death. It also has a short half-life of approximately 70,000 years so it cannot be used for dinosaur fossils.

Radioactivity is also used in medicine, most commonly to fight cancer. Gamma rays can be aimed at tumors and used to kill the cells, reducing the tumor's size. It is also used in x-rays and CT scans to obtain a detailed view of the interior of the body.

Decay times for radioactive isotopes are measured by their half-life. The half-life is the amount of time it takes for half of the isotopes in a sample to change. This can occur quickly for some elements and take billions of years for others. It is not possible to predict exactly when each change will occur, but scientists can make reasonable estimates for the amount of time until change. If a scientist has 40kg of a radioactive isotope with a half-life of 30 min and she goes to lunch for 30 minutes, 20kg will remain when she returns. In another 30 minutes, there will be 10kg, and 30 minutes after that there will be 5kg. Half of the sample decays every 30 minutes.

Nuclear Chemistry - Half-life Calculations

Below is the equation relating half-life to initial chemical amount, final chemical amount, and time.

N(t)=N0​(21​)t1/2​t​

Where

• N(t) = final amount

• N0​ = initial amount

• t = time elapsed

• t1/2​ = half-life

All terms must be in the same unit (ex: grams and years). The following examples show how to calculate half-life as the mass of an element changes over time.

Example 1: Potassium-40 has a half-life of 1.25 billion years, which makes it useful for dating ancient rocks. What percentage of potassium-40 is remaining in a meteorite that is 2.45 billion years old?

The problem provided the half-life and time (age in billion years) and is looking for the final amount percentage. We can assume an initial amount of 100%.

N(t)=N0​(21​)t1/2​t​

N(t)=100(21​)1.252.45​

N(t)=100(21​)1.96

N(t)=25.7

After 2.45 billion years, there will be 25.7% of the original potassium-40 in the meteorite.

Example 2: A 10,000-year-old fossilized leaf is found to contain 87 g of carbon-14. Given that the half-life of carbon-14 is 5,730 years, how much carbon-14 did the leaf contain when it was alive?

The problem provided the half-life, final amount, and time (age in years) and is looking for the initial amount (N0​).

N0​=N(t)/(21​)t1/2​t​

N0​=87/(21​)573010000​

N0​=87/(21​)1.7452

N0​=291.66

The leaf originally contained 292 g carbon-14.

Example 3: Nitrogen-13 is a useful radiotracer in medical imaging because it has a half-life of about 10 minutes. How long does it take for a sample of 5 g of N-13 to decay to 25% of the original mass?

The problem provided the half-life and the change in chemical mass over time and is looking for the amount of time elapsed.

The first half-life of N-13 reduces the mass by 50% in 10 minutes.

The second half-life of N-13 reduces the mass in half again to 25% in 10 minutes.

t = 20 minutes

Example 4: Uranium-235 has a half-life of 704 million years. How long does it take for a 270 kg sample of U-235 to decay to 105 Kg?

N(t)=N0​(21​)t1/2​t​

Use natural logarithms to solve for time (t).

N0​N(t)​=21​×t1/2​t​

ln(N0​N(t)​)=ln(21​)×t1/2​t​

t=ln(N0​N(t)​)/ln(21​)×t1/2​ 

t=ln(270105​)/ln(21​)×704 

t=959.25 million years

Radioactivity

Radioactivity occurs when an atomic nucleus releases energy, often changing the number of protons in the nucleus. The protons identify each type of atom, so changing the number of protons changes what element it is. The act of changing the subatomic particles releases radiation in the form of particles and energy.

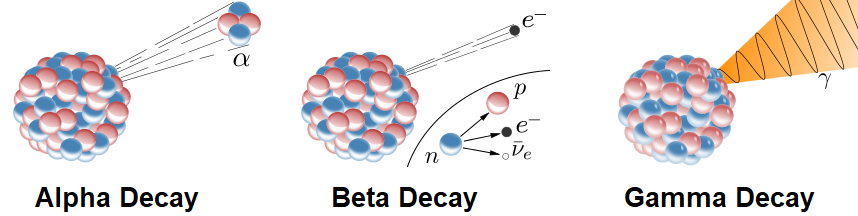
Three types of decay can occur:

• Alpha Decay - The nucleus emits an alpha particle with 2 protons and 2 neutrons, leaving the rest of the nucleus behind. The atomic number of the isotope decreases by 2 and the mass number decreases by 4. The alpha particle carries off energy in the form of kinetic energy.

• Beta Decay - A neutron changes into a proton by emitting an electron and a neutrino from the nucleus. The atomic number of the isotope increases by 1 but the mass number stays the same. The electron and neutrino carry off energy in the form of kinetic energy.

• Gamma Decay - Electromagnetic energy is released from the nucleus in the form of a gamma ray. The atomic number and mass number of the isotope do not change.

Nuclear Energy: Fission

In nuclear fission, heavy elements, like uranium, split apart into lighter elements. In doing so, they release a great deal of energy, which is used in power plants to heat water, turn a turbine, and run a generator. Nuclear reactors operate on nuclear fission and are used worldwide to generate electricity. One concern with nuclear fission power plants is where and how to store the highly radioactive byproducts that last for thousands of years.

Uranium-235 is the principal fuel used in fission reactors. In a fission reaction, a neutron strikes a ²³⁵U nucleus forming an unstable ²³⁶U atom which quickly splits apart into products such as ⁸⁹Kr, ¹⁴⁴Ba, and three neutrons. ²³⁵U and ²³⁶U are isotopes of uranium. The released neutrons strike other uranium nuclei, triggering a chain reaction. The mass of the products is less than the mass of the original ²³⁵U and the missing mass transforms into energy during the reaction.

Nuclear Energy: Fusion

In nuclear fusion, light elements fuse together to create heavier elements. Nuclear fusion requires extreme temperatures and pressures, and currently occurs only in stars, including our sun. Controlled fusion does not occur naturally on earth, although we have been trying to recreate it, as it could be an excellent solution to our future energy needs. Helium, a light gas without any radioactivity, is the byproduct of a hydrogen fusion reaction, making fusion a safer choice than fission.

Fusion powers our sun. In the core of the sun, two isotopes of hydrogen, deuterium (²H) and tritium (³H) fuse, forming energetic helium (⁴He) and neutrons, as shown. As with fission, the mass of the reactants is greater than the mass of the products, with mass transforming to energy during the process.

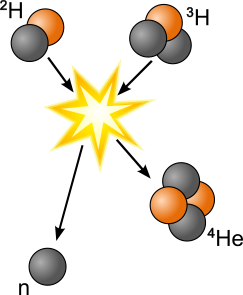
In fission, elements break apart into lighter elements (think "fissure" for cracking apart).

In fusion, lighter elements come together to form heavier elements (think "fuse" for coming together).

Atomic spectra

The specific colors of light absorbed and emitted by an atom due to electron transitions between energy levels.

Absorption spectrum

The range of wavelengths or energies that an atom will absorb from light passing through it, resulting in dark lines in the spectrum.

Emission spectrum

The range of wavelengths or energies that an atom will emit due to electrons falling down in energy levels, resulting in specific lines in the spectrum.

What Are Atomic Spectra?

Everything in the world has a certain color. But how is the color determined? It depends on what's the structure of the things, what is their composition. Learn what the atomic spectra is, how it was discovered, and what its uses are.

Atomic Spectra can be defined as the fingerprints of the different elements of the world. It is an array of lines that are produced by light that is emitted or absorbed because of their chemical composition. All of the objects surrounding us are composed of different elements of the periodic table which have a specific patron. Because these lines are unique the spectra are used to determine the composition of multiple things, even stars!

Special artifacts called spectrometers are needed to appreciate these patterns. They work by measuring the interaction of light with different materials. There are different classifications between spectra. Depending on the energy interaction, it can be divided in emission, seen as a black stripe with colored lines and the absorption spectrum would be a colorful stripe with black lines.

An example of an atomic spectra is a rainbow, when we appreciate one in the sky, we believe that we are seeing a continuous image that goes from purple to red, but the reality is that if we have enough detail of the image, we can observe certain black lines. This happens because the sun does not emit a continuous spectrum, when it gets mixed with the gas forming the clouds - an absorption spectrum!

History of the Absorption and Emission Spectrum

The first concepts of spectroscopy and the spectrums come from Newton who discovered that if you put white light through a glass prism you observe a variety of colors - the same colors observed in the rainbow.

The History of the spectrum as we know it today comes from the mid-1700s when Thomas Melvill noted that burning alcohol changes its color when salt is added. Later, William Hyde Wollaston observed that the Sun has dark lines in its spectrum. These lines were better studied by Joseph von Fraunhofer in 1814 who also observed that different stars had specific black lines in their specter. Fraunhofer also invented the spectroscope changing the glass prism by a diffraction grating. Fraunhofer is considered one of the most important scientists in the spectrometry area. Furthermore, in 1817 Fraunhofer thoroughly observed the Sun spectrum and discovered that it is not continuous, the missing parts are called the Fraunhofer lines.

Then, in 1849 Foucault, realized that the absorption black lines matched the colorful emission lines. The biggest discovery was by Gustav Robert Kirchhoff and Robert von Bunsen in 1860. They discovered that the spectrum is distinctive for each element.

In 1868 Anders Ångström studied the solar spectral lines; this was a key element to the introduction of quantum physics concepts by Max Planck in 1900 that helped to explain the difference between the lines.

Defining Absorption Spectrum

When light goes through a gas or material, a line of colors appears with black lines in between the colors. This is known as the absorption spectrum; it can also be defined as the graphic representation of the amount of energy absorbed by a specific material from an incident white light. The white light is decomposed in the range of visible light that goes from purple, the highest energy, to red - the one with the lowest energy.

Defining Emission Spectrum

An emission spectrum is the complementary part of the absorption spectrum. Instead of having a colorful stripe with black lines, it will have a black stripe with certain color lines. The way to obtain it is heating the gas or material. When this happens, the electrons will absorb energy and change energy levels, but when it cools down, the energy will go down again, and the electrons will lose energy that will be emitted as a light. Contrasting with the absorption spectra occurs when the objects absorb energy from a different source.

An important note is that the color lines appreciated in the emission spectrum have the same energy levels as the black lines observed in the absorption spectrum.

Defining Emission Spectrum

An emission spectrum is the complementary part of the absorption spectrum. Instead of having a colorful stripe with black lines, it will have a black stripe with certain color lines. The way to obtain it is heating the gas or material. When this happens, the electrons will absorb energy and change energy levels, but when it cools down, the energy will go down again, and the electrons will lose energy that will be emitted as a light. Contrasting with the absorption spectra occurs when the objects absorb energy from a different source.

An important note is that the color lines appreciated in the emission spectrum have the same energy levels as the black lines observed in the absorption spectrum.

Energy Levels of Absorption vs. Emission

The basis of atomic spectra is the composition of the elements, which are formed by electrons orbiting at a certain distance away from the nucleus of the atoms. The electrons can only move in certain levels of energy or shells. The shells are named levels K, L, and M according to their energy steps and can be represented as circles or lines, shown in the image below. This distance works similar to steps on stairs. Moving each step requires a fixed amount of energy. When electrons acquire enough energy, they move to a step above (excited state), when they go down a level, they emit energy. It is important to remember that if they do not have enough energy the electrons will not move from their level and if they do not have enough energy to lose, they won't go down a step. In general, when the electrons move from the ground state to excited state, they will absorb energy that will represent as black lines in the emission specter and when the electrons go down a level, they emit colors according to the energy liberated, observed as the color lines in the emission specter.

Defining emission spectrum

An emission spectrum is the complementary part of the absorption spectrum. Instead of having a colorful stripe with black lines, it will have a black stripe with certain color lines.

The way to obtain it is heating the gas or material. When this happens, the electrons will absorb energy and change energy levels, but when it cools down, the energy will go down again, and the electrons will lose energy that will be emitted as a light. Contrasting with the absorption spectra occurs when the objects absorb energy from a different source.

An important note is that the color lines appreciated in the emission spectrum have the same energy levels as the black lines observed in the absorption spectrum.

Uses of Atomic Spectra

Atomic spectroscopy has several uses. Its capacity of determining which elements compose a material is important for areas like metallurgy, determining the pureness of a sample and the quality of the extraction methods. It is also useful in the pharmaceutical industry, helping to assess the impurities that exit in a specific medicine. In addition, is important in areas like astronomy to assess objects in the outer space and determine its composition. This attribute is also useful in mechanical engineering or material science. In the case of environmental sciences and analytical chemistry is important to know if samples are contaminated with an element that can be harmful for the environment or for the experimentation.

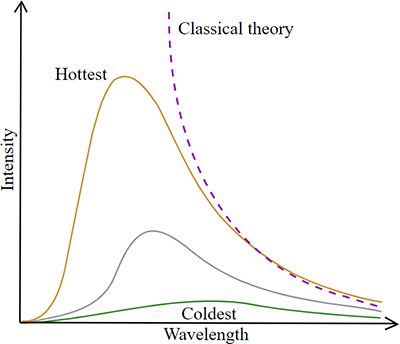
Blackbody Radiation

All objects with a temperature above 0K emit electromagnetic radiation. A blackbody absorbs all energy that falls on it and is called a perfect absorber. The intensity of radiation emitted by a blackbody at different frequencies depends only on the temperature of the blackbody, as shown below. Many real objects are modeled as blackbodies.

Emission Spectra

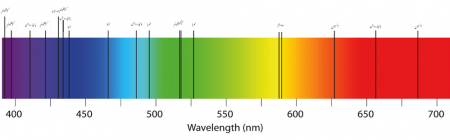
An emission spectrum is produced when a very low-pressure gas is heated. The emission spectrum of an element is a series of colored lines of different wavelengths (or frequencies). The spectrum of each element is unique.

The spectrum appears when electrons in the atom fall from higher energy to lower energy states. For example, the bright red line in the emission spectrum of hydrogen, below, is caused by electron transitions from the 3^rd to the 2^nd energy level in the atom. The blue line is caused by electron transitions from the 4^th to the 2^nd energy level.

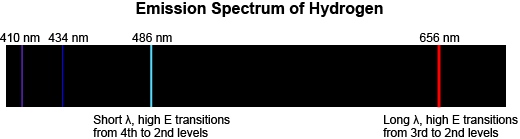
The greater the energy released during an electron transition, the shorter the wavelength of the emitted light.

Absorption Spectra

The spectra of the sun and stars include the entire rainbow of colors because the various atoms in stars are very hot and close together. When the starlight passes through gas clouds in space, or through the outer layer of the sun, electrons in the gas atoms are excited and certain frequencies are absorbed. An absorption spectrum has black lines at these absorbed frequencies.

For example, the absorption spectrum above indicates the light has passed through hydrogen gas. The entire spectrum is visible except at the energies of the electron transitions in hydrogen (compare this with the emission spectrum of hydrogen).

Astronomers use absorption spectra to determine which elements are present in space and in stars.

An emission spectrum has bright lines produced when electrons fall to lower energy levels. An absorption spectrum has dark lines produced when electrons transition to higher energy levels.

The Quantum Model and Matter Waves

The fixed electron orbits of the Bohr model works to explain the spectrum of hydrogen but does not quite work for the other elements. The quantum model of the atom better explains the spectra of other elements.

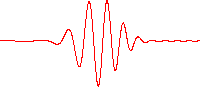
Louis deBroglie hypothesized that since light waves have particle behavior, perhaps particles would have wave behavior. Experiments with electron beams confirmed that electrons diffract like waves.

The deBroglie wavelength relates the wavelength 𝜆 of a particle of matter to its momentum, mv, and Planck's constant, h:

λmatter​=mvh​

All matter demonstrates both wave and particle properties, but since the value of Planck's constant h is very small and the mass of everyday objects is very large, the wavelength of everyday objects is very tiny. Because of this, we experience only their particle nature. When the mass is very small, like that of an atom, quantum effects become important.

In the quantum model of the atom proposed by Erwin Schödinger, electrons are treated as matter waves rather than as particles. The quantum model explains that electrons can exist only in certain orbits because there they form standing waves.

Recall that standing waves occur on a string when the length of the string matches some number of half-wavelengths because of constructive and destructive interference.

In a similar way, an electron wave experiences constructive interference with itself as it travels around the orbit. All other orbital radii produce destructive interference. Some of the allowed quantum electron orbitals are shown with bright colors in the representation of a hydrogen atom, below.

The basis of quantum mechanics is that both light and matter have dual natures: waves and particles. Only very small particles of matter display their wave nature.

About Bohr Model: Introduction

Fire photons to determine the spectrum of a gas. Observe how an absorbed photon changes the orbit of an electron and how a photon is emitted from an excited electron. Calculate the energies of absorbed and emitted photons based on energy level diagrams. The light energy produced by the laser can be modulated, and a lamp can be used to view the entire absorption spectrum at once.

Photoelectric effect

The emission of electrons from a material when light of certain frequencies shines on the surface of the material

Photons

A quantum, or discrete amount, of light energy.

Wavelength

The distance between crests of waves, such as those of the electromagnetic spectrum.

Frequency

How many waves can pass a given point per second, measured in Hertz (Hz)

Photoelectron

The electron that is ejected during the process of photoelectric interaction

Photoemissive

release of electrons from a metal, resulting from the exposure to light or radiation, gives insight to the metals internal structure.

Planck Units

These units are considered fundamental to theoretical physics.

Planck's constant

a number used to calculate the radiant energy (E) absorbed or emitted by a body based on the frequency of radiation

Dual Nature of Light - Early Models

Toward the end of the 1600s, scientists argued whether light is a series of particles or waves. Sir Isaac Newton argued for particles. Christiaan Huygens argued for waves. The observed properties of reflection and refraction of light could be explained with either model.

About 100 years later, Thomas Young devised an experiment (the double slit experiment) that proved that light is a wave. Young shined a light beam through two very small slits onto a screen. Instead of two bright lines, expected if light were a series of particles, Young observed a wave interference pattern on the screen. The series of bright and dark lines that Young observed was the constructive and destructive interference pattern of the light waves that emerged from the slits. Particles do not produce interference patterns, so scientists concluded that light is a wave.

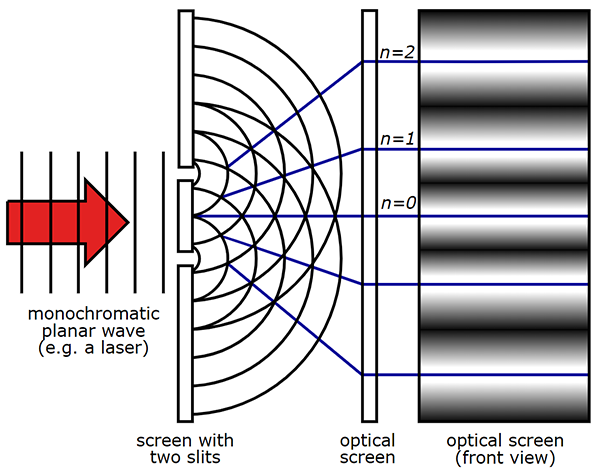
About 100 years after Young's experiment, scientists made some puzzling observations. Max Planck investigated the energy in sunlight and compared it with theoretical values. The wave theory implied that Earth should receive a huge amount of high-frequency ultraviolet light energy from the sun. This was not the case.

Another mystifying experiment of that time was the photoelectric effect. When certain light was shined on metal, electrons escaped from the metal.

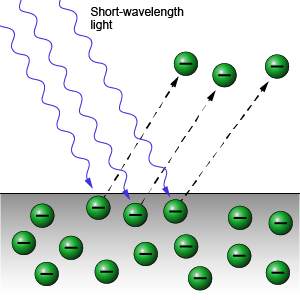
The energy in the light was transferred to the electrons, but this observation did not match the wave theory.

The wave model of light predicted that with a brighter light, electrons would emerge with more energy and that with low-frequency light, the energy would accumulate over time until some electrons were eventually released.

Instead, experiments showed that a brighter light released more electrons, but they were not more energetic. Only higher-frequency light gave the electrons more energy. No electrons were released at all when the light frequency was below a certain value, no matter how long the experiment lasted. These results are summarized in the table.

Dual Nature of Light - The Mystery Explained

In 1905, Albert Einstein proposed an explanation for both mysteries: a particle model of light. He explained that the energy in light is quantized, that is, it comes only in chunks (like particles). Each particle's energy was proportional to the constant h and the frequency, f, of the light.

Eone particle​=hf

The constant, h=6.63×10−34sm2kg​, was later called Planck's constant and each particle or quanta of light was called a photon. Notice that the value of Planck's constant is very small so each chunk of energy is very small.

The photoelectric effect was explained because when light shines on metal, each electron absorbs the energy of one and only one photon. If the frequency of the light, and therefore the photon's energy, is high enough, the electron will escape. The electron can not slowly gain energy from constant low frequency light. The minimum frequency for which electrons are ejected is the threshold frequency of the metal.

In the particle model of light, a photon's energy cannot be shared among electrons, nor can an electron "store up" energy from multiple photons.

The experimental results and the particle nature explanations of the photoelectric effect are detailed in the table below.

Today, we understand that light has a dual nature. It behaves like both a wave and a particle. This is the basis of quantum physics.

Young's double-slit experiment verified the wave nature of light. The photoelectric effect verified the particle nature of light. We now know that light has a dual nature.

The Uncertainty Principle

In 1927, Werner Heisenberg discovered a fundamental property of nature that applies to all wave-like systems, including quantum mechanical waves. This property is the uncertainty principle.

The uncertainty principle can be stated many ways because of how wave properties are related. One of the most common ways of expressing the uncertainty principle is that it is impossible to exactly determine both the position x and the momentum p of a particle at a given time.

To better understand the uncertainty principle, consider the dual nature of an electron in the table below.

The Observer Effect

The observer effect states that no one can make an accurate measurement of the position of an object without disturbing its velocity. For example, when observing a small particle with an electron microscope, the electrons from the microscope will bombard the object and change its position or velocity.

The observer effect is often used to explain the uncertainty principle, but it is important to note that the uncertainty principle is not a function of our technology, but a true property of nature. Very precise instruments, such as gravitational wave detectors, function only because of the uncertainty principle. Very small particles do not obey the laws of classical physics, such as Newton's laws.

The uncertainty principle states that it is impossible to know a particle's state exactly. It is a fundamental fact of nature and not something that will change with better technology.

special relativity

Einstein's radical theory that revolutionized physics in the early 20th century

space-time

Einstein's concept that space and time are not uniquely independent, but that time is truly the 4th dimension of the universe

time dilation

clocks moving relative to an observer are measured by that observer to run more slowly; t2 = y * t1

length contraction

the length of an object is measured shorter when it is moving relative to the observer than when it is at rest; L2 = L1/y

General Relativity

Gravitational attraction between masses is a result of the nearby masses; gravity has wavesTheories of Relativity

Albert Einstein is well known for many of his works, including his  theories of relativity Relativity is the concept that motion, space, and time are relative to each other rather than absolute. For example, motion can affect time, and gravity can affect the speed of light. This is related to the concept of space-time, which views space as four-dimensional rather than three-dimensional, with time being the fourth dimension. Hermann Minkowski proposed space-time in 1908 in response to Einstein's work.

Einstein's two theories of relativity are special relativity (relativity without gravity, which is an attractive force due to the effect of an object on space-time) and general relativity (relativity with gravity). One historical difference between special relativity and general relativity is when they were developed. After scientists proved in the late 1800s that the speed of light does not follow classical mechanical rules, in 1905, Albert Einstein postulated that the speed of light in a vacuum is a universal constant. This is true in special relativity but not in general relativity. Einstein proposed the theory of general relativity in 1916 that generalized his theory to account for the effect of gravity on light.

Theory of Special Relativity

Even though special relativity is a special case of general relativity, Einstein came up with special relativity first. Special relativity is essentially general relativity in the simple case of no gravity. Special relativity is applicable to objects and waves in an inertial reference frame which means a frame of reference that is not accelerating (i.e., the velocity does not change). This idea is connected to Newton's first law (i.e., the law of inertia),which states that a body at rest will remain at rest, and a body in motion will continue to move in a straight line at a constant velocity unless an external force acts upon it. In other words, a body undergoes no acceleration when there is no net force acting upon it. So, there is no effect of gravity on one object or wave relative to another object or wave in an inertial reference frame.

The theory of special relativity accounts for the constant speed of light in this inertial frame of reference. In other words, light travels at a constant rate as long as it moves in a straight line through space with no surrounding mass. The major postulates of special relativity are:

• The principle of relativity: The laws of physics are consistent in all inertial reference frames.

• The invariance of the speed of light: The speed of light is constant in an inertial reference frame, as light in an inertial reference frame is not affected by gravity.

See Figure 2 for a diagram illustrating the principle of relativity. Massive objects warp the fabric of space-time, and gravity distorts the lines of travel of other objects.

Theory of General Relativity

The theory of general relativity is largely concerned with gravity. Gravity, unlike the other fundamental forces is macroscopic. As a result, it is concerned with large-scale phenomena like black holes, planetary motion, and the life cycles of stars. General relativity is fundamentally different from special relativity because it accounts for the effects of gravity. General relativity generalizes both special relativity and Newton's law of gravitation (i.e., gravity is a force due to the bending of space-time). Large, massive objects, like black holes and stars, warp space-time and thereby affect the motion of other objects. See Figure 3 for an image of curved space-time.

Relativity states that motion, space, and time are affected by each other. This may seem counterintuitive or simply false. For example, in classical mechanics, velocities in the same direction can be added. So, if a person is walking at 2 meters per second and they throw a ball forward at 10 meters per second, the ball's initial horizontal velocity would be 12 meters per second. However, relativity has been supported experimentally; A.A Michelson and Edward W. Morley showed that velocity vector addition does not work for light.

Special Relativity vs. General Relativity

Special relativity is applicable if the objects and waves are in the same inertial frame of reference, while general relativity does not have that requirement. Similarly, special relativity assumes a constant speed of light, while general relativity does not. The key difference between special and general relativity is that special relativity ignores the effects of gravity because it has no effect in an inertial reference frame, while general relativity accounts for the effect of gravity on light.

Special Relativity - Time Dilation, Length Contraction

While thinking about light, Albert Einstein realized that our measurements of time, distance, and mass (inertia) are not the fixed quantities we thought they were. According to the theory of special relativity, as an object's speed increases, as measured from the frame of reference of a stationary observer, the object's time t slows down (time dilation), lengths L or distances decrease (length contraction), and mass m, or inertia, increases, all by a factor of gamma (γ). Gamma varies with the object's speed.

These transformations are called the Lorentz transformations and represent the time interval, length, and mass of the object when it is at rest relative to the observer.

Frame of Reference

Special relativity deals with the effects that occur due to the relative motion between an object and an observer. Special relativity refers to measurements that are made from the point of view or frame of reference of an observer who is not moving with the object. The observer is considered to be "at rest" even though this phrase really has no meaning (think about it: we are not even at rest on Earth's surface).

Relativity at Everyday Speeds

These relativistic effects occur at all speeds but are noticeable only when speeds approach the speed of light. 

One of the peculiar aspects of Einstein's theory of special relativity is that the length of objects moving at relativistic speeds undergoes a contraction along the dimension of motion. An observer at rest (relative to the moving object) would observe the moving object to be shorter in length. That is to say, that an object at rest might be measured to be 200 feet long; yet the same object when moving at relativistic speeds relative to the observer/measurer would have a measured length which is less than 200 ft. This phenomenon is not due to actual errors in measurement or faulty observations. The object is actually contracted in length as seen from the stationary reference frame. The amount of contraction of the object is dependent upon the object's speed relative to the observer.

The animations below depict this phenomena of length contraction. In each animation a spaceship is moving past Earth at a high speed. The spaceship would be measured to be 200 feet in length when at rest relative to the observer.

Spaceship Moving at the 10 % the Speed of Light

Spaceship Moving at the 86.5 % the Speed of Light

Spaceship Moving at the 99 % the Speed of Light

Spaceship Moving at the 99.99 % the Speed of Light

Note that the length contraction is only significant when the object is moving at relativistic speeds - i.e., speeds which are a significant fraction of the speed of light. Furthermore, note that the contraction only occurs in the dimension of the object's motion. If the object is moving horizontally, then it is the horizontal dimension which is contracted; there would be no contraction of the height of the object. This information is summarized in the table below.

While special relativity says that no physical object can move faster than light through space-time, general relativity shows that space-time itself can and does move. Furthermore, it places no limit on how fast space-time itself can move.

So, it is theoretically possible for a spaceship to contract the space-time in front of it while expanding the space-time behind it. The result is that the ship would ride a wave of space-time within a bubble of normal space, much as a surfer rides an ocean wave. The wave of space-time could move faster than light, but the ship would not, so it would not experience the consequences of special relativity.

In 1995, physicist Miguel Alcubierre showed that this was theoretically possible within Einstein's theories. This work supported the science fiction concept of faster-than-light travel. The theory remains under examination.

Einstein showed that the laws of physics hold true in any frame of reference, such as rest, constant motion, or acceleration. Special relativity dealt with rest and constant motion. It showed that no object could move faster than the speed of light, and objects approaching the speed of light would experience time dilation, length contraction, mass increase, and momentum increase. It also showed that mass and energy were the same.

In general relativity, Einstein showed that gravity was a distortion of space-time by mass and energy. General relativity predicted that gravity would slow time and bend light. Curving space-time has theoretically allowed for faster-than-light travel through a warp drive because space-time itself moves. Einstein's theories have been confirmed many times.

Applications of Special and General Relativity

When learning about the difference between special and general relativity, it can be helpful to consider some examples of how the theories are applied in real life. Some applications of special and general relativity include:

• GPS relies on ultra-accurate satellite clocks. High-accuracy GPS, which gives information with centimeter-level precision, requires the clocks to be correct to within 20-30 nanoseconds. The effects of relativity, if not accounted for in the engineering of the GPS clocks, would throw off the clocks by thousands of nanoseconds. Thus, the satellite clocks must be synchronized with clocks on Earth, as their positions in space put them much further from the Earth's center of gravity, and they experience time slightly differently than Earth clocks.

• Scientists used the redshift (stretching) of electromagnetic waves to determine the rate at which the universe expands. This is essentially the Doppler effect for light waves as opposed to sound waves. The Doppler effect is the observed change in the frequency of a wave due to the wave's source moving relative to the detector. As the universe expands, electromagnetic waves seem to have longer wavelengths than they actually do, as predicted by special relativity.

• Similarly, radar guns, which are used to detect whether and by how much a car is driving over the speed limit, rely on the Doppler effect. A radar gun emits radio waves, which bounce off of a passing car and detect the returning waves. The faster the car travels, the larger the shift in the frequency of the waves. Thus, the radar gun can calculate the car's speed from the amount of wavelength shift detected.

  photoelectric effect

  The emission of electrons from a material when light of certain frequencies shines on the surface of the material. Showed that the frequency of light determines the energy of the e- released. Led to the rise of quantum theory

  Max Planck

  theorized that light is made up of small, high speed bursts of energy of a specific size, known as quanta(plural) or quantum(singular), which could be measured.

  matter wave theory

  electrons have both wave and particle properties

  wave-particle duality

  electrons and light can behave as both a wave and a particle

  Heisenberg uncertainty principle

  states that it is impossible to determine simultaneously both the position and velocity of an electron or any other particle. The act of measure one value changes the other. Therefore the location of e- is expressed as a probability.

  Quantum Theory is the branch of physics that studies atomic and subatomic particles, and their associated phenomena. It was developed in the early 1900s by Max Plank, and the theory was extended by many physicists including Einstein, Heisenberg, Dirac, and Schrodinger.

  Quantum Theory

  Quantum physics is made up of many different theories collectively called quantum theory. Quantum mechanics, another name for quantum physics, was first proposed by several key founders in the early 1900s. The following are some key developments and concepts by these founders:

  • In 1900, Max Planck published a theory that energy would be grouped into finite portions or quanta. This concept is called quantization. He proposed this idea to explain why observations of black body radiation would not behave in the way predicted by classical laws of physics.

  • In 1905, Albert Einstein postulated that not only energy is quantized but also light and other forms of radiation are quantized into finite packets called photons.

  • In 1913, Niels Bohr theorized that the hydrogen atom (and therefore also other atoms) had energy levels only in discrete values, quantized values. He also proposed that predictions of the quantum realm based on mathematical probabilities does predict reality and that attempting to observe the atomic realm empirically will change or jeopardize quantum interactions.

  • In 1924, Louis de Broglie proposed the principle of  wave -particle duality. This theoretical principle predicts that waves and particles both have properties like each other. At times, particles behave and have properties like waves and waves behave and have properties like particles. Fundamentally, at the subatomic level, matter and waves are the same.

  • In 1927, Werner Heisenberg published what would become known as the Heisenberg uncertainty principle. His theoretical opinion was that both the position and the momentum of a subatomic particle cannot be measured at the same time. If the position is measured then no accurate observation of the momentum can be made and vice versa.

  • In 1935, Erwin Schrodinger created his thought experiment that became known as Schrodinger's Cat In this thought experiment, there is a cat that is locked in a box awaiting the result of a possible subatomic event. The unobserved cat could be in a paradox of being considered both dead and alive at the same time until observed. This shows that the concepts of quantum mechanics does not make sense in the larger scale of the real world. Schrodinger theorized that physical events occur only in terms of probability of the event; there is no definitive certitude to physical events.

    In summation, quantum theory proposes that particles act like waves and can be described in terms of the probability wave functions of their position, velocity, and mass. All properties of matter are, at their foundation, based on probability. According to quantum mechanics, there is a possibility of all kinds of seemingly impossible things, such as that of being able to walk through a wall, but the probability of the matter in the wall vanishing into empty space is so low it would only happen once in many lifetimes of the universe.

    Quantum particles are described by a wavefunction, and when we observe them (that is when we measure them) we can alter their state. Quantum particles can be found in a superposition of states, but we do not know which one until we measure them: this is best exemplified by the hypothetical Schrodinger's cat, a thought experiment consisting of putting a cat on a box with poison, which results in the cat being in a superposition of dead and alive, with the observer not knowing until they open the box.

    Some important principles of Quantum theory include the Heisenberg uncertainty principle, which indicates that we cannot know with perfect accuracy both the position and the velocity of a quantum particle, and the existence of entanglement, a long-range interaction effect that interacting quantum particles can have on one another.

    Quantum Applications

    Although classical physics works when dealing with the huge numbers of atoms in larger objects, only quantum rules can explain what really happens with both everyday objects and tiny particles.

    One application of quantum theory that we experience nearly every day is the red glow of a burner on a stove. Because of quantum principles, we understand that the burner glows in visible light frequencies because of the allowed electron transitions. If quantum physics did not hold, the burner would glow with damaging x-rays or ultraviolet rays.

    Fluorescent lights contain mercury vapor. The light they produce is the emission spectrum of mercury, which is a quantum effect.

    Atomic clocks are based on quantum theory. Time is measured by the frequency of oscillations of electrons as they jump from one energy level to another. Notice the dual nature in the description of what happens. Electrons are thought of as particles, yet they have a wave property, frequency, that constrains them to certain energy levels.

    Photoelectric sensors operate because of the photoelectric effect. The semiconductors used in today's computers operate because of the band of empty space between electron energy levels.

    One eerie effect of quantum properties is entanglement. Entangled particles, even when separated by astronomical distances, somehow share information with each other instantly. Because of this, quantum encryption is now possible (with some practical limitations on distance). Quantum encryption uses polarized photons as a key to the code. Reading the key changes the polarization of the photons. If someone tries to unlock the key, entangled photons will reveal that the polarization has changed.

    Quantum computers are currently under development and will be much quicker than today's binary computers.