pV Graphs

Equation - U = Q - W

The equation ( U = Q - W ) relates internal energy (U), heat added to the system (Q), and work done by the system (W).

Mind Map: pV Graphs and Relevant Information

Main Branches

1. Definition of pV Graphs

• Pressure-Volume (pV) representation

• Visualizes thermodynamic processes

• Relationship between pressure (p) and volume (V)

2. Types of Processes

• Isothermal Process

  • Constant temperature

  • Hyperbolic curve

• Adiabatic Process

  • No heat exchange

  • Steeper curve than isothermal

• Isobaric Process

  • Constant pressure

  • Horizontal line

• Isochoric Process

  • Constant volume

  • Vertical line

3. Area Under the Curve

• Represents work done (W)

• Positive area: work done by the system

• Negative area: work done on the system

4. First Law of Thermodynamics

• Equation: ΔU = Q - W

  • ΔU: Change in internal energy

  • Q: Heat added to the system

  • W: Work done by the system

• Implications of pV graphs on ΔU

  • Work done affects internal energy changes

  • Heat transfer influences system state

5. Key Concepts Deduced from pV Graphs

• Work Calculation

  • Area under the process curve

• Heat Transfer Analysis

  • Relationship between Q and W

• Internal Energy Changes

  • Understanding system behavior during processes

6. Applications of pV Graphs

• Engine cycles (e.g., Carnot, Otto)

• Refrigeration cycles

• Understanding real gases vs. ideal gases

Conclusion

pV graphs are essential tools in thermodynamics, providing insights into work, heat transfer, and internal energy changes during various processes.

Basic analysis of a pV graph:

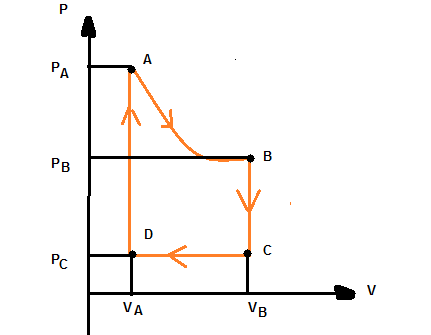
AB: Isometric Process

isometric Process - temperature remains constant.

• Pressure increases

• Volume Decreases

• Temperature is constant

• Transfer of heat in/out system so slow, thermal equilibrium is maintained

• Work done by system

• Since U = 0, W = Q

Effects on U = Q - W:

1. Internal Energy (U): For an ideal gas, internal energy depends only on temperature. Since temperature is constant, ( U ) does not change. = 0

2. Heat (Q): Heat must be added to the system to maintain constant temperature as pressure increases and volume decreases. So, +ve

3. Work (W): Work done on the system is positive when volume decreases.

   +ve

Thus, in this scenario, ( Q ) must equal ( W ) to keep ( U ) constant.

BC: Isochoric Process

Isochoric Process - Volume remains constant

• Volume Constant, W = 0

• Pressure Decreasing

• Temperature Constant

• Heat flows out the system, so Q = -ve

• No work done so U = Q

• Therefore as Q = -ve, U = -ve

CD: Isobaric Process

Isobaric Process - Pressure remains constant

• Pressure constant

• Volume decreasing

• Temperature decreasing

• Gas contracting so work being done on system, W = -ve

• Heat flows out, Q = -ve

• Since temperature is decreasing, U = -ve

DA: Isochoric Process

Isochoric Process - Volume remains constant

• Volume Constant, W = 0

• Pressure increasing

• Temperature Constant

• Heat flows into the system, so Q = +ve

• No work done so U = Q

• Therefore as Q = +ve, U = +ve

Adiabatic Process

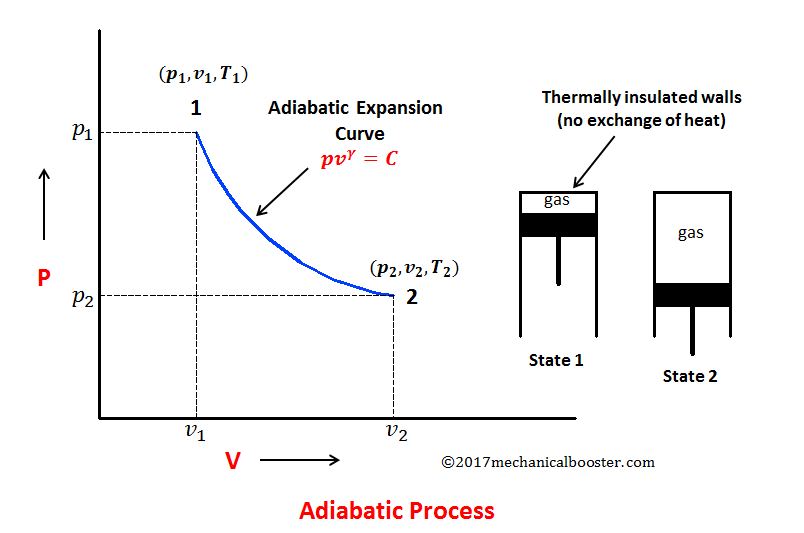
Adiabatic Process - heat exchange is zero

• Volume Increases,

• Pressure decreases

• Temperature Increases

The adiabatic equation describes these relationships:

PV^γ = constant

Since an adiabatic process has no heat transfer (Q = 0), the equation simplifies to:

ΔU = −W

• If work is done on the gas (compression), internal energy increases, leading to a rise in temperature.

• If work is done by the gas (expansion), internal energy decreases, causing a drop in temperature.

This shows that in an adiabatic process, all energy changes come from work done, not from heat exchange.