Chapter 1: Units, Physical Quantities, and Vectors

• Physics is an experimental science.

  • Physicists observe the phenomena of nature and try to find patterns that relate these phenomena.
  • These patterns are called physical theories or, when they are very well established and widely used, physical laws or principles.

• No theory is ever regarded as the final or ultimate truth. The possibility always exists that new observations will require that a theory be revised or discarded.

• Problem-Solving Strategy for solving Physics Problems:

  • 1**. IDENTIFY** the relevant concepts.
  • 2.SET UP the problem.
  • Given the concepts you have identified and the known and target quantities, choose the equations that you’ll use to solve the problem and decide how you’ll use them.
  • 3.EXECUTE the solution.
  • Study the worked examples to see what’s involved in this step.
  • 4.EVALUATE your answer
  • Compare your answer with your estimates, and reconsider things if there’s a discrepancy.

• In physics a model is a simplified version of a physical system that would be too complicated to analyze in full detail.

• Any number that is used to describe a physical phenomenon quantitatively is called a physical quantity.

  • Example: weight, height etc.

• When we measure a quantity, we always compare it with some reference standard.

  • Such a standard defines a unit of the quantity.
  • The meter is a unit of distance, and the second is a unit of time.

• Some units of length, Mass and time:

  

• <<An equation must always be dimensionally consistent.<<

• An uncertainty in the measurement is also called the error because it indicates the maximum difference there is likely to be between the measured value and the true value.

  • The uncertainty or error of a measured value depends on the measurement technique used.

• When a physical quantity is described by a single number, it is a scalar quantity.

• In contrast, a vector quantity has both a magnitude and a direction in space.

  • The simplest vector quantity is displacement.
  • Displacement is simply a change in the position of an object.
  • Displacement is a vector quantity because we must state not only how far the object moves but also in what direction

• A vector with the same magnitude but in the opposite direction is known as a negative vector.

• When two vectors and have opposite directions, whether their magnitudes are the same or not, we say that they are antiparallel.

• The magnitude of a vector quantity is a scalar quantity (a number) and is always positive

  

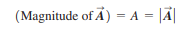
• A vector can never be equal to a scalar because they are different kinds of quantities.

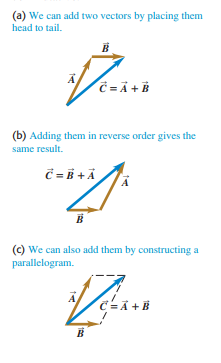
• Suppose a particle undergoes a displacement A followed by a second displacement B .

  • The final result is the same as if the particle had started at the same initial point and undergone a single displacement C.
  • We call displacement the vector sum, or resultant, of displacements and We express this relationship symbolically as

  C= A+B

  • If we make the displacements and in reverse order, with first B and second A, the result is the same.
  • 

• Multiplying a vector by a positive scalar changes the magnitude (length) of the vector, but not its direction.

• Multiplying a vector by a negative scalar changes its magnitude and reverses its direction.

• A vector can be divided into its horizontal component( Ax) and a vertical component (Ay).

  

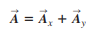
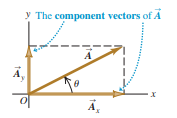
• Components are not vectors. The components and of a vector are just numbers; they are not vectors themselves.

• Imagine that the vector originally lies along the x axis and that you then rotate it to its correct direction, as indicated by the arrow in figure below on the angle theta.

  • If this rotation is from the +x axis toward the +y axis, then theta is positive
  • If the rotation is from the +x axis toward the -y axis, theta is negative.

• Thus the +y axis is at an angle of 90°, the at 180°, and the at 270° (or If is measured in this way, then from the definition of the trigonometric function).

  

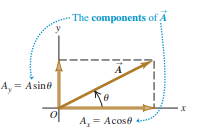
  The trigonometric functions for this vector and theta are:

  

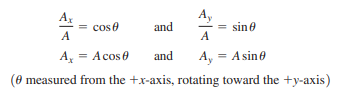
• Unit vectors describe directions in space. A unit vector has a magnitude of 1, with no units.

  • The unit vectors i,j and k aligned with the x-, y-, and z-axes of a rectangular coordinate system, are especially useful.

    

  

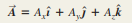
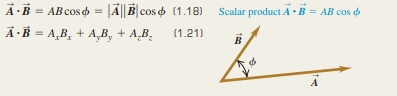
• The scalar product C=A.B of two vectors A and B is a scalar quantity.

  • It can be expressed in terms of the magnitudes of A and B and the angle phi between the two vectors, or in terms of the components of A and B.

  • The scalar product is commutative.

  • The scalar product of two perpendicular vectors is zero.

    

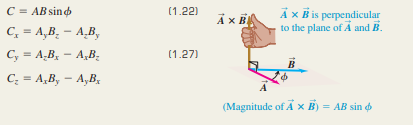
• The vector product C=AxB of two vectors A and B is another vector.

  • The magnitude of depends on the magnitudes of A and B and the angle phi between the two vectors.

  • ==The direction of the vector product is perpendicular to the plane of the two vectors being multiplied, as given by the right-hand rule.==

  • The components of the vector product can be expressed in terms of the components of A and B.

  • The vector product is not commutative.

  • The vector product of two parallel or antiparallel vectors is zero.

    

\