Stacks and Queues

Data Structures Discussed

• Variable-length arrays

• Linked lists

  • Advantages and disadvantages of both structures discussed.

  • Focus on the implementation of how to store and organize data.

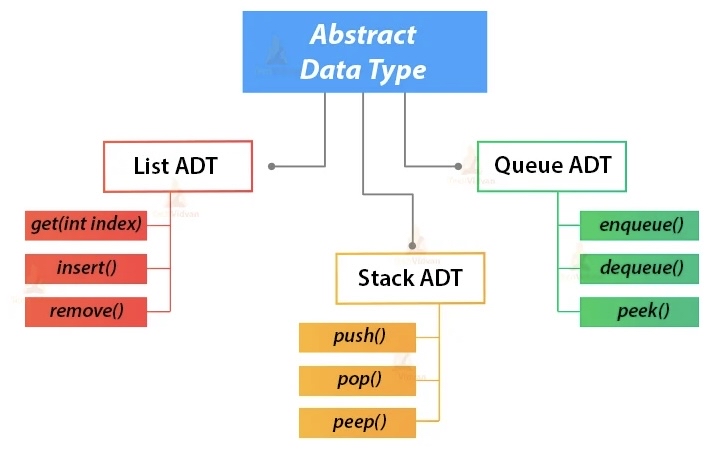
Abstract Data Types (ADT)

• Conceptual model emphasizing operations over implementation.

• Often referred to as interfaces in different contexts.

Operations on Data Structures

• Detailed discussions on how elements can be added or removed.

• Imposing rules on element operations leads to specific abstract data types:

  • Push and pop operations limited to specific ends.

Stacks and Queues

• Both are abstract data types with restrictions on operations.

• Maintain linear data structures with rules on growth and shrinkage.

Stacks

• Follows the Last In, First Out (LIFO) principle.

• Only the topmost element needs to be tracked for operations.

Common Stack Operations

• push(val): Adds an element to the stack.

• pop(): Removes the top element and returns it.

• peek() or top(): Returns the top element without removing it.

• is_empty(): Checks if the stack is empty.

• is_full(): Checks if the stack has reached its capacity.

Implementing Stacks

• Can be implemented using linked lists or arrays.

• Each implementation's running time complexity varies based on design.

• Linked List Implementation:

  • Stack elements represented as nodes.

  • Methods include adding/removing through head management.

• Array Implementation:

  • Requires predefined size (capacity).

  • Manual management of stack properties ensures operations function as expected.

Stack Applications

• Infix and Postfix Notation: Used for evaluating mathematical expressions.

• Call Stack Management: For function calls and recursion simplifications.

Queues

• Follows First In, First Out (FIFO) principle.

• Tracks both the front and the back of the queue.

Common Queue Operations

• enqueue(val): Adds an element to the rear.

• dequeue(): Removes and returns the front element.

• peek() or front(): Returns the front element without removal.

• is_empty(): Checks if the queue has no elements.

• is_full(): Checks the capacity status.

Implementing Queues

• Similar to stack implementations, queues can use linked list or array structures.

• Each operation's complexity and efficiency are critical factors in design.

Circular Arrays

• Presented as an efficient solution to standard array limitations.

• Implications include improved operational efficiencies and risk of index overflow.

Queue Applications

• CPU Scheduling: Determines process priorities for CPU execution.

• Queueing Theory: Evaluates scenarios like supermarket or amusement park processes.

Conclusion

• Discussions on data structure implementations and their efficiencies are vital for understanding stacks and queues in computer science.

• Future considerations in assignments will involve applying these principles in practical programming tasks.