Big Idea 3: Algorithms and Programming
Algorithms
- Algorithm: is a set of steps to do a task.
- Recipes are algorithms.
- They are a set of steps to prepare food.
- Instructions for taking medicine make up an algorithm.
- Directions to get from one location to another are an algorithm.
- Computer science algorithms: are the set of steps to solve a problem or complete a task.
- Algorithms: are implemented with software.
- Examples are programs to:
- Calculate grade averages
- Run the air conditioner when the room temperature reaches 78°F
- Calculate the shortest route from home to school on your GPS
- Algorithms have the potential to solve many problems once the programs are written for them to run.
- Section of code: may work independently or can be used with other programming modules.
- These program modules read in values, make computations as needed, and produce output to automate processes.
Data Abstraction
A popular way of defining abstraction is information hiding.
Just as related program statements are bundled together, related program variables can be bundled together.
Such abstractions allow us to think of the data within a program hierarchically.
A list is an example of data abstraction.

A list is a data type that holds a collection of values.
aList[3, 7, 11]
aList is described as a "list of integers."
Within a list, when accessing its parts using an integer index, aList[1] gives us the value 3, aList[2] = 7, and so on. Lists allow for data abstraction in that we can give a name to a set of memory cells. For instance, in a colorList, a list that holds three colors ['red', 'blue', 'green'] instead of using three separate variables, colori, color2, etc., one variable colorList holds all the three variables. Each of the contents of the list is accessed by changing the index value.
Variables
- Variables: are placeholders for values a program needs to use.
- A program may need variables for numbers, both integers and real numbers, as well as text fields and Boolean values.
- Variables can be used in expressions, both mathematical and textual.
- An important aspect of variables is naming them well.
- Variables are data abstractions because we do not need to know the details of how and where the values are stored in memory.
Strings
- Strings: are text fields that are just a series of characters and are denoted with quotation marks around the string field.
- Any character, number, or symbol can be part of a string.
- When numbers are part of a string, then they will be considered to be text, like in a street address.
- In this case, you cannot use them in calculations because they are text fields, not numbers.
Assignment Statements
To assign a value to a variable, the assignment operator is used.
In many programming languages, a single equals sign, =, is used as the assignment operator.
The variable name is always on the left of the ← sign.
The programming language will evaluate the right hand side of the assignment operator and then place the value into the variable on the left-hand side of it.

The previous value stored in a variable is overwritten by a new assignment statement.
- In this example, a variable named score is assigned the value 10.
- It is then assigned the value 11.
- The value 10 is gone and no longer available.
Expressions: are calculations to be evaluated to an answer or single value.
In computer science, the value is then assigned to a variable if the value will be needed later.
It also could be displayed on a screen or printed.

You will get an error if you write:
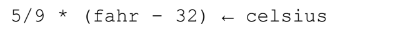
The variable must be on the left and the assignment arrow points left.

The expression will be evaluated and loaded into the variable celsius.
P Parentheses
E Exponents
M Multiplication
D Division
A Addition
S Subtraction
Boolean Values
Boolean values: are one of the foundations of computer code.
Understanding Boolean is important for writing correct, readable, and efficient code.
Boolean values can only be true or false, needing only one bit to represent its value.
Relational operators are used with Boolean values.
These are just like in your math class:
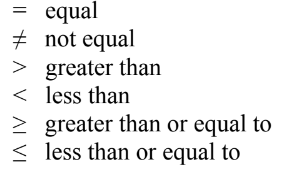
Program Statements
- All programs can be written using a combination of only three types of statements.
- These statements are used over and over and can be combined for more complex needs, but there are only three.
Sequential
- These are statements that are executed as written in order in the program.
- As we start writing our programs, a code statement has an action that will be executed when the program is run.
- Once a statement is complete, the next statement is run.
- Naturally, they have to be in the correct order to accurately complete the algorithm.
Selection Statements
These are a key component to many programs.
They use the “if (condition)” structure, and the evaluation of the condition uses Boolean values.
As we know, Booleans can only be either true or false, so the program statements associated with the condition only run when the condition at that moment evaluates to “true.”
This changes the flow of the program from every statement running sequentially to filtering out some of the code that will execute, based on the Boolean value.

Notice that the code to be executed when the condition is true is surrounded by the curly braces, { }, in the “Text” version.
The code within the braces is indented, which helps with readability.
It also makes it easier to see if you are missing a closing brace }!
Iterative
- Iterative statements: are also referred to as repetitive statements or loops.
- This type of programming statement also changes the sequence of lines of code that are executed.
- Code that is associated with these statements repeats as many times as specified before continuing with the rest of the program.
Repeat Until (Condition) Loop
The REPEAT UNTIL loop has a condition to evaluate at each iteration of the loop.
The loop will continue to run while the condition evaluates to “false.”
This is similar to how an IF statement works except the condition for the IF statement must evaluate to true for it’s code to execute.

Combining Algorithms: One of the key features of algorithms is that once they are created, you can use them over and over, combine them for more complex problem solving, or modify them for a new use.
Nested Conditionals
In a program or code snippet where there is an IF statement within another ser of IF statements, these are called nested IF statements.
When the outer IF statement is executed, the inner IF statement may also get executed.
This allows for the program solution to evaluate another expression after determining the results of a previous decision.

Common Algorithms
Determining the maximum or minimum number from two or more numbers.
The pseudocode for the maximum of two numbers is:
- Compare the numbers.
- Store the larger number as the maximum.
For the minimum of two numbers:
- Compare the numbers.
- Store the smaller number as the minimum.
If you have more than two numbers, a computer can still only compare two at a time.
One number would be the current largest (or smallest), and the other would be the next number to compare it to.
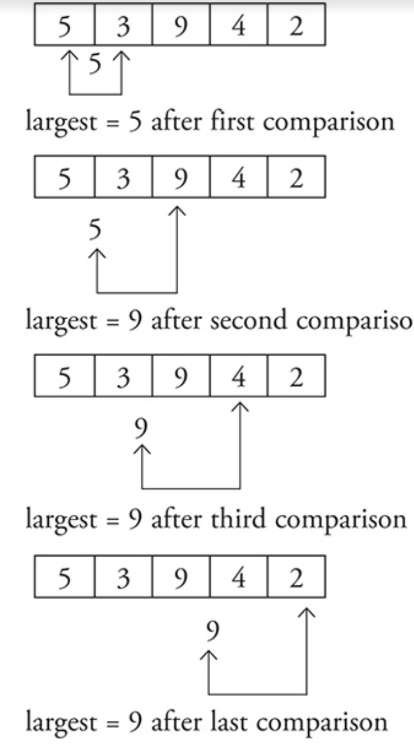
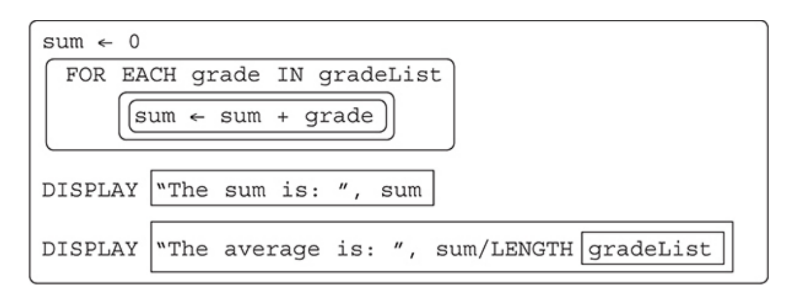
Another common algorithm is calculating the sum and average of a group of numbers.
This is fairly straightforward since it is a concept you have already learned in math class.
One key element to remember is that you need to keep count of how many numbers you have added together so you will be able to calculate the average.
Lists
Lists: are a collection of items, such as a grocery list or a playlist of music.
A list in a program can be a collection of numbers, words, phrases, or a combination of these.
Usually a list only contains one type of data in a single list, but some programming languages do allow different types of data in the same list.
Lists provide the ability to store more than one value in the same variable, separated by commas, when the variable is defined as a list.
Lists are also called arrays in some programming languages.



List Indices
Individual items in a list are called elements and are accessed by position using an index.
Index positions: are always integers and are enclosed within square brackets [index].

Built-in Methods
Most programming languages will have built-in procedures, or “methods,” of common functionality to use with lists.
Adding an item to a specific position in a list.
The INSERT command causes elements to the right of the indicated index position, i, to shift right one position to make room for the new element.

Appending an item to the end of the list.
The APPEND command will add the new element to the end of the list, so no index position is needed.
The size of the list increases by one.

Removing an item from a list.
The REMOVE command deletes the element at the provided index position and shifts the remaining elements one position to the left.
The size of the list decreases by one.

Length: The length of a list is the number of elements in the list.

Checking Each Item in a List
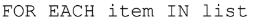
The above statement is a loop that will automatically repeat the code for each element in the list.
- This is called traversing a list.
The programmer chooses the name for the iteration variable “item”.
Each pass of the loop will assign the value of the next element in the list to the variable “item”.
Processing lists with a FOR EACH loop takes advantage of features of both structures.

Common Algorithms
There are algorithms that are frequently needed for processing lists with iteration.
These include finding the largest or smallest number in a list.
Here is an example using a REPEAT UNTIL loop with a list of grades.

Another common algorithm is finding the sum and average of the values in a list.
Searching
Searching: deals with finding the needed element from everything in the dataset or determining that it is not there.
Linear Search: Linear searches, also called sequential searches, check each individual record, starting at the beginning and going to the end, one after the other in order to either find the desired data or to determine it is not in the dataset.

Binary Search: Binary searches are far more efficient than linear searches.
- However, data must be sorted to use a binary search.
- The binary search is considered a “divide and conquer” algorithm because it divides the dataset into two equal parts.
Procedures
Procedures: are also called functions in some programming languages.
These are sections of code that will be executed only when they are called by the main program or another procedure.
They must be defined in a program before they can be used in the program.

Parameters/Arguments
- The use of parameters can make procedures more flexible.
- Parameters: allow the calling program to send values to the procedure.
- They are passed to the procedure as arguments when the procedure is called.
- The values sent to the procedure can be different each time, making the procedure more flexible through the ability for multiple calls to the same section of code.
Calling a Procedure
- When the procedure is “called,” the program will pause at that location and execute the code in the procedure.
- When the procedure finishes, control returns back to the line of code where the call occurred.
- This is another programming structure that modifies the sequential flow of the program.
- Procedural abstraction: You only need to know the name of the procedure, the number and type of parameters, and the output to expect.
Random Values
Random number generator programs: are useful tools for writing software, mainly in designing games.
A random number generator picks a number at random out of a range of values.

Return
Procedures: have an optional feature called a return statement.
The return statement has two uses.
One purpose is to end a procedure before the end of the code is reached.
No other code in the procedure will be executed after the return statement.
The other use is to send a value back to the calling program.

Built-in Procedures: Built-in procedures are prewritten and tested code that are included with the programming language.
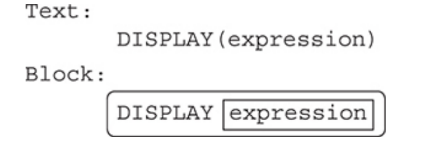
DISPLAY(): DISPLAY() is a built-in procedure used for this course on the exam.
- We do not know how this procedure is coded, only that we can use it multiple times, pass it different types and values to print, and that it works.
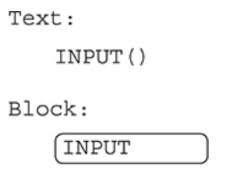
INPUT(): It accepts data from the user, usually from the keyboard.
- When the programming language sees this command, it will pause the program and wait for something to be typed on the keyboard.
APIs and “Libraries”
- For each programming language, there are prewritten programs to provide commonly needed functionality, and these programs are stored in libraries, which are folders with several programs.
- API stands for “Application Programming Interface.”
- The API documentation provides the information needed to set up the interface and use the newly connected software.
Random
- Generating random numbers is a frequently needed feature in programs.
- Most programming languages have a library of prewritten code for a variety of random number generators.
- RANDOM needs two values passed to it using arguments, the beginning and ending range for the selected random number.
- Simulations: Simulations are designed to represent and mirror the real world for testing.
Analyzing Algorithms
- An instance of a problem is a specific example.
- A decision problem has a yes or no answer.
- An optimization problem is one that should find the best solution for the problem.
Algorithm Efficiency
- The efficiency of algorithms deals with resources needed to run it in terms of how long it will take and how much memory will be needed.
- This becomes especially important with extremely large datasets, and efficiency is usually stated in terms of the size of the input.
- Efficiency: can be determined by mathematically proving it and informally measured by actually running it on datasets of different sizes and measuring how long it took and the memory resources needed.
Limits of Algorithms
- Algorithms have limits, and there are some problems for which we do not have efficient enough algorithms to solve.
- These algorithms can’t run in a reasonable amount of time with our current technology.
- Heuristic approach: This is an approach that may not be optimal or the best but is close enough to use as a solution.
Street Traffic Models
- Simulation, as a tool, is used when studying traffic systems when the system is too complicated.
- The advantage of simulation tools is that they provide visual demonstrations for different scenarios, both present and future.
- These models are necessary tools for planning and operating traffic systems, as they help to predict the behavior of vehicles in the traffic system.
Solar Activity Models
- All engineering disciplines use simulation tools that help them study phenomena specific to their field of expertise.
- Simulations are now part of the design process.
- Models require considerable time and effort to develop.
- Simulation models are used to study the solar system.
- Modeling and simulation is a powerful method to evaluate the design of a space system.
- Simulation modelsrepresent valuable knowledge that scientists use to build systems to explore space. \n
Undecidable/Unsolvable Problems
- Decidable problem: is one where an algorithm can be written that results in a correct “yes” or “no” answer for all inputs.
- Determining if a number is prime is an example of a decidable problem.
- Undecidable problem: does not have an algorithm that can give a correct “yes” or “no” for all cases of the problem.