
Unit 4 Light/Energy levels & Configuration >
Wavelength, Frequency, and the Speed of Light
λ (lambda) = wavelength
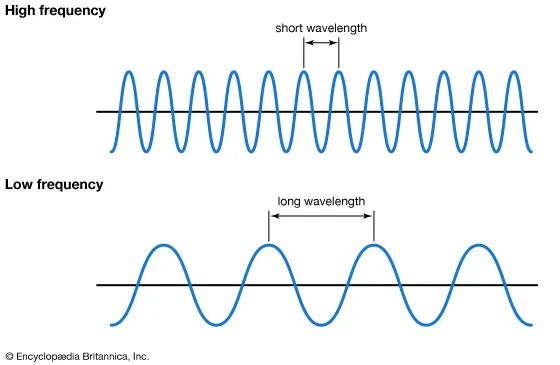
A wavelength is a distance between where a wave’s shape repeats. In other words, it is the distance from crest to crest (Top to top) or trough to trough (bottom to bottom). An example is included in the diagram below.
ν (nu) = frequency
The frequency is the number of waves repeated over a certain unit of time, waves with high frequency have shorter wavelengths, and this is the opposite for low-frequency waves.
C= speed of light
The speed at which light propagates through certain materials. In the air, the speed of light is:
3 × 10^8 m / s
E= energy
h= Planck’s constant
Planck’s constant is a fundamental foundational constant in quantum mechanics-
6.626 x 10^-34
C = λ x ν
Speed of light = wavelength x frequency
E = h x ν
Energy = Planck’s constant x frequency
E = h c/λ
Energy = (Planck’s constant x Speed of light ) / wavelength
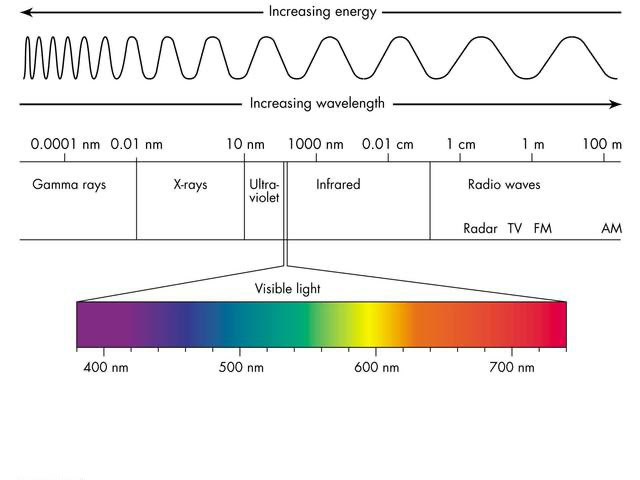
The Electromagnetic Spectrum [describes all kinds of light]
The wavelengths of light cover a very wide and broad spectrum, with only a small portion of it being able to be detected with human eyes. This is the visible light spectrum, and the visible light spectrum includes the colors of the rainbow (each color has a different wavelength).
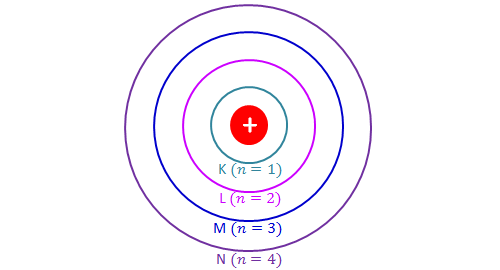
Position of Electrons
We know that electrons are negatively charged subatomic particles which reside outside of the nucleus, but scientists use various other terms to describe the location of an electron in an atom. Such terms include:
Energy level- An energy level is a fixed distance from an atom's nucleus where electrons exist. They determine the chemical properties of the element and are also called electron shells.
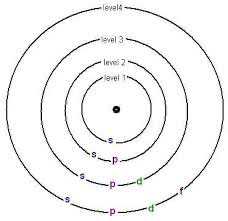
Sublevel (Subshell)- Each energy level has its own sub-levels which are represented as s, p, d, and f. These sublevels can all hold different amounts of electrons, s holding the least, and f holding the most.

Orbital- Sub-levels contain orbitals, which are the spaces where an electron is held. One orbital can contain two electrons and there are different amounts of orbitals in each sub-level (this can be seen in the table below).
Spin- Spin is a type of angular momentum, and is when the electron spins around its axis.
Energy level | sublevel | orbitals in sublevel | electrons in the sub-levels (each level has two electrons) |
|---|---|---|---|
n=1 | S | 1 | 2 |
n=2 | S; P | 1;3 | 2; 6 |
n=3 | S; P; D | 1;3;5 | 2; 6; 10 |
n=4 | S; P; D; F | 1;3;5;7 | 2; 6; 10; 14 |
Now that a basis is built, we can finally understand how photons (/energy and frequency of light) are emitted from an electron. Each time an electron jumps to a higher level, it needs to absorb a specific amount of energy. It will keep jumping to the top, then it will relax and go back down, emitting energy at the same time.
Ground state- the point at which an electron has the lowest energy, this is typically energy level n=1
Bohr’s Model vs. Quantum Mechanical Model

Bohr’s model claims that electrons have a fixed orbit, while the Quantum Mechanical model (newer model) says that atoms have orbitals, these include:
S orbitals/S sub-level: sphere- one possible shape, lowest energy)
P: dumbbell-shaped: electrons can appear anywhere in the dumbbell shape (2 possible shapes)
D: 5 possible shapes
F: 7 possible shapes (highest energy)
Trends of the Periodic table
Atomic radius
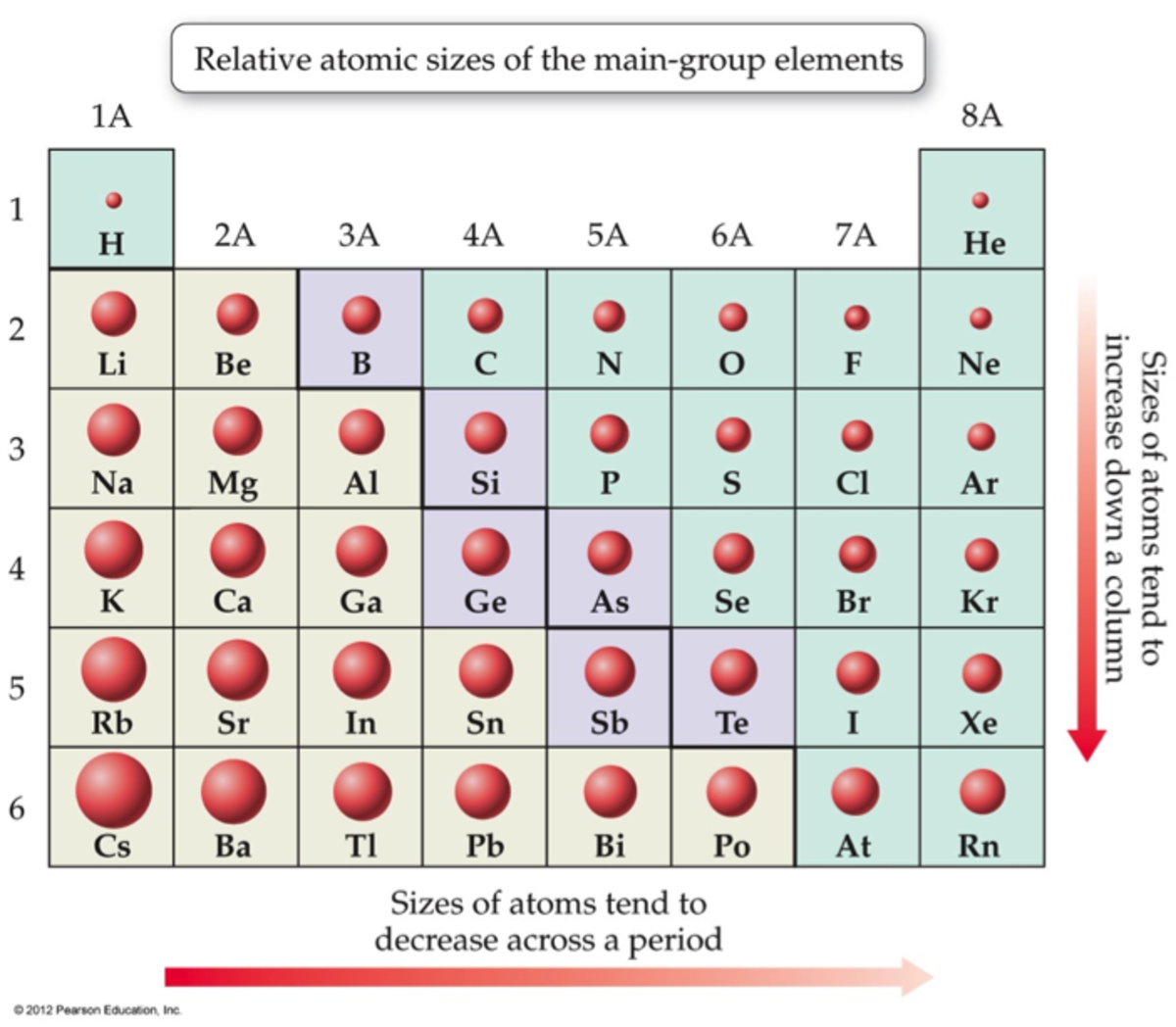
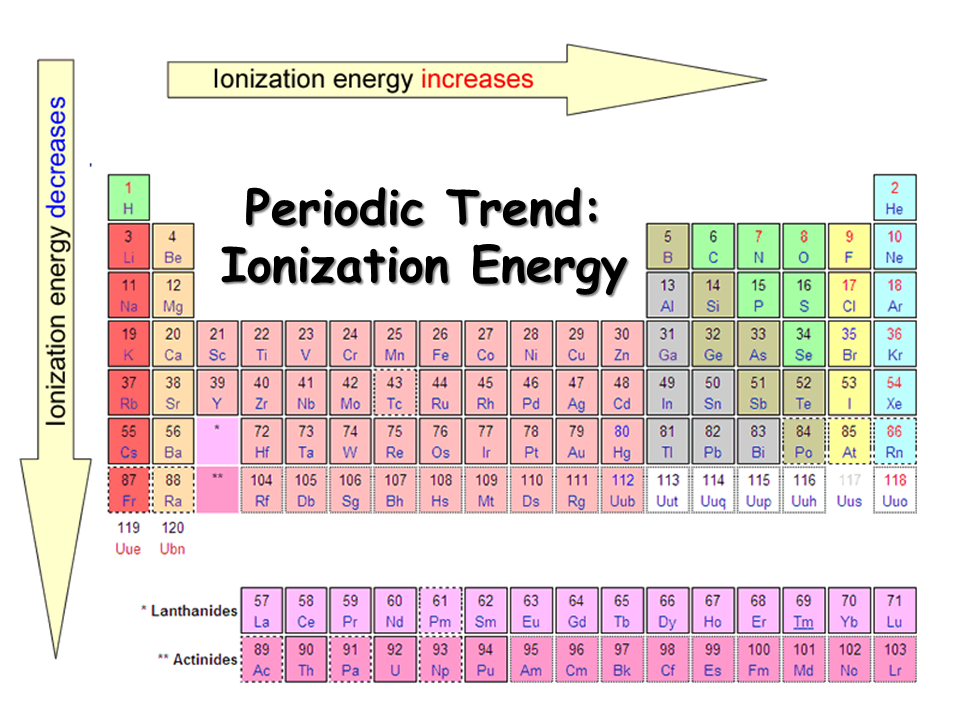
Ionization energy
Electronegativity
-The ability of an atom or a functional group to attract electrons toward itself
-Electronegativity values generally increase from left to right across the periodic table and generally decrease from top to bottom of a group.
-The highest electronegativity value is for fluorine
-The smaller the size of an electron, the stronger the ability to attract electrons, because the statical electrical force becomes stronger when the distance between the outermost shell is getting smaller

Electron and Noble Gas Configuration
Electron configuration is a way to represent the distribution of electrons of an atom/molecule.
To best demonstrate this method, we will be using the diagonal method. 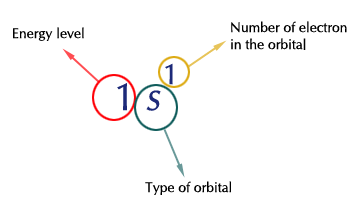 In order to best utilize energy, electrons will fill orbitals with lower energy first.
In order to best utilize energy, electrons will fill orbitals with lower energy first.
 Moving in the order in which the arrows point, orbitals are slowly filled to the number of electrons. As an example, the element nitrogen has 7 electrons. Referring to the previous table, we know how many electrons each of the sub-levels (s, p d, and f) hold. Therefore, we can follow the diagonal rule and slowly continue until there are 7 electrons in total. We start with 1s^2, then 2s^2, and finally 2p^3. Although the p sub-level can hold 6 electrons, there are not enough electrons left so we just put the number of remaining electrons.
Moving in the order in which the arrows point, orbitals are slowly filled to the number of electrons. As an example, the element nitrogen has 7 electrons. Referring to the previous table, we know how many electrons each of the sub-levels (s, p d, and f) hold. Therefore, we can follow the diagonal rule and slowly continue until there are 7 electrons in total. We start with 1s^2, then 2s^2, and finally 2p^3. Although the p sub-level can hold 6 electrons, there are not enough electrons left so we just put the number of remaining electrons.
If we need to find the electron configuration for an ion, we figure out how many electrons there are.
Note: elements with the same number of electrons are referred to as isoelectronic
Orbital Diagram
An orbital diagram helps portray electrons in an atom.
For each sub-level in the electron configuration, we can represent the number of orbitals and electrons. Using nitrogen as an example again, we can create:
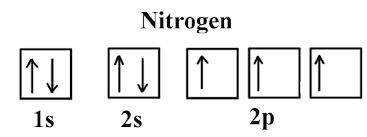
One box represents that the S sub-level has one orbital, while the opposite-facing arrows represent the electrons. (Note- an orbital can contain two electrons, and those two electrons must have opposite spins, which is the reason why the arrows point in the opposite direction in this diagram).
When having a sub-level with more than one orbital, you must draw arrows facing the same direction with no more than one arrow per box until all boxes are filled. Then, you can draw another arrow in the same box, facing the opposing directions.
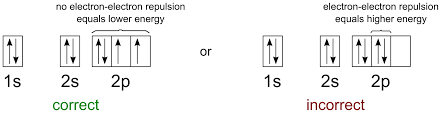
Noble Gas Configuration
This method of configuration helps shorten the representation of electrons by showing the elemental symbol of the noble gas in the prior row, and then the configuration of the rest of the electrons. In order to do this, you need to know the blocks of sub-levels on the periodic table:
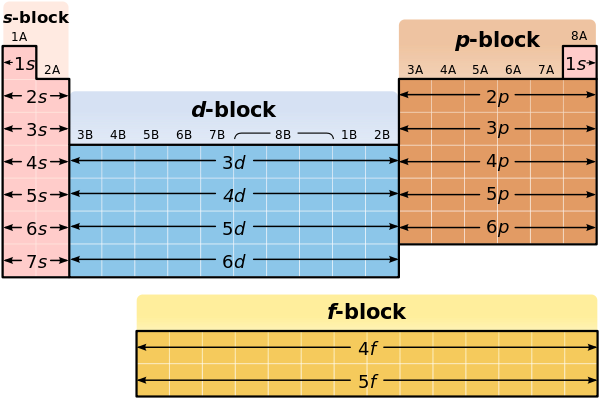
First, you could find the electron configuration of an element, and identify which configuration has the same position as the noble gas prior to that element. You would then write that noble gas in brackets, and include the configurations after.
OR…
If we configure Phosphorous, we would take the noble gas from the previous row [Ne], and then use its place on the periodic table to write the configurations for the rest of the electrons. It is the third element down(represents energy level). Due to how it is all the way in the p block, we will need to first go through the s and d blocks. To do this, we take its energy level and use the maximum number for the row placement for both blocks → 3s^2, 2d^10. Since 2d^10 does not exist on the periodic table, we only use 3s^2. Lastly, we find its place in the P block which is where potassium is and get its configuration: 3p^3.
Lastly, we put this all together.
Noble gas→ [Ne] 3s² 3p³ <--superscript 3: 3rd element on row of P block
↑
The threes are there because it is the 3rd element down
Important note: An exception is that in the d block, you need to subtract an energy level from its configuration because it starts on the fourth row. This is because they require more energy to fill up.
Example: Technetium has the noble gas configuration of [Kr] 5s^2 4d^5, instead of [Kr] 5s^2 5d^5 because of this rule.
Unit 4 Light/Energy levels & Configuration >
Wavelength, Frequency, and the Speed of Light
λ (lambda) = wavelength
A wavelength is a distance between where a wave’s shape repeats. In other words, it is the distance from crest to crest (Top to top) or trough to trough (bottom to bottom). An example is included in the diagram below.
ν (nu) = frequency
The frequency is the number of waves repeated over a certain unit of time, waves with high frequency have shorter wavelengths, and this is the opposite for low-frequency waves.
C= speed of light
The speed at which light propagates through certain materials. In the air, the speed of light is:
3 × 10^8 m / s
E= energy
h= Planck’s constant
Planck’s constant is a fundamental foundational constant in quantum mechanics-
6.626 x 10^-34
C = λ x ν
Speed of light = wavelength x frequency
E = h x ν
Energy = Planck’s constant x frequency
E = h c/λ
Energy = (Planck’s constant x Speed of light ) / wavelength

The Electromagnetic Spectrum [describes all kinds of light]
The wavelengths of light cover a very wide and broad spectrum, with only a small portion of it being able to be detected with human eyes. This is the visible light spectrum, and the visible light spectrum includes the colors of the rainbow (each color has a different wavelength).

Position of Electrons
We know that electrons are negatively charged subatomic particles which reside outside of the nucleus, but scientists use various other terms to describe the location of an electron in an atom. Such terms include:
Energy level- An energy level is a fixed distance from an atom's nucleus where electrons exist. They determine the chemical properties of the element and are also called electron shells.

Sublevel (Subshell)- Each energy level has its own sub-levels which are represented as s, p, d, and f. These sublevels can all hold different amounts of electrons, s holding the least, and f holding the most.

Orbital- Sub-levels contain orbitals, which are the spaces where an electron is held. One orbital can contain two electrons and there are different amounts of orbitals in each sub-level (this can be seen in the table below).

Spin- Spin is a type of angular momentum, and is when the electron spins around its axis.
Energy level | sublevel | orbitals in sublevel | electrons in the sub-levels (each level has two electrons) |
|---|---|---|---|
n=1 | S | 1 | 2 |
n=2 | S; P | 1;3 | 2; 6 |
n=3 | S; P; D | 1;3;5 | 2; 6; 10 |
n=4 | S; P; D; F | 1;3;5;7 | 2; 6; 10; 14 |
Now that a basis is built, we can finally understand how photons (/energy and frequency of light) are emitted from an electron. Each time an electron jumps to a higher level, it needs to absorb a specific amount of energy. It will keep jumping to the top, then it will relax and go back down, emitting energy at the same time.
Ground state- the point at which an electron has the lowest energy, this is typically energy level n=1
Bohr’s Model vs. Quantum Mechanical Model

Bohr’s model claims that electrons have a fixed orbit, while the Quantum Mechanical model (newer model) says that atoms have orbitals, these include:
S orbitals/S sub-level: sphere- one possible shape, lowest energy)
P: dumbbell-shaped: electrons can appear anywhere in the dumbbell shape (2 possible shapes)
D: 5 possible shapes
F: 7 possible shapes (highest energy)
Trends of the Periodic table
Atomic radius

Ionization energy

Electronegativity
-The ability of an atom or a functional group to attract electrons toward itself
-Electronegativity values generally increase from left to right across the periodic table and generally decrease from top to bottom of a group.
-The highest electronegativity value is for fluorine
-The smaller the size of an electron, the stronger the ability to attract electrons, because the statical electrical force becomes stronger when the distance between the outermost shell is getting smaller

Electron and Noble Gas Configuration
Electron configuration is a way to represent the distribution of electrons of an atom/molecule.
To best demonstrate this method, we will be using the diagonal method.  In order to best utilize energy, electrons will fill orbitals with lower energy first.
In order to best utilize energy, electrons will fill orbitals with lower energy first.
 Moving in the order in which the arrows point, orbitals are slowly filled to the number of electrons. As an example, the element nitrogen has 7 electrons. Referring to the previous table, we know how many electrons each of the sub-levels (s, p d, and f) hold. Therefore, we can follow the diagonal rule and slowly continue until there are 7 electrons in total. We start with 1s^2, then 2s^2, and finally 2p^3. Although the p sub-level can hold 6 electrons, there are not enough electrons left so we just put the number of remaining electrons.
Moving in the order in which the arrows point, orbitals are slowly filled to the number of electrons. As an example, the element nitrogen has 7 electrons. Referring to the previous table, we know how many electrons each of the sub-levels (s, p d, and f) hold. Therefore, we can follow the diagonal rule and slowly continue until there are 7 electrons in total. We start with 1s^2, then 2s^2, and finally 2p^3. Although the p sub-level can hold 6 electrons, there are not enough electrons left so we just put the number of remaining electrons.
If we need to find the electron configuration for an ion, we figure out how many electrons there are.
Note: elements with the same number of electrons are referred to as isoelectronic
Orbital Diagram
An orbital diagram helps portray electrons in an atom.
For each sub-level in the electron configuration, we can represent the number of orbitals and electrons. Using nitrogen as an example again, we can create:

One box represents that the S sub-level has one orbital, while the opposite-facing arrows represent the electrons. (Note- an orbital can contain two electrons, and those two electrons must have opposite spins, which is the reason why the arrows point in the opposite direction in this diagram).
When having a sub-level with more than one orbital, you must draw arrows facing the same direction with no more than one arrow per box until all boxes are filled. Then, you can draw another arrow in the same box, facing the opposing directions.

Noble Gas Configuration
This method of configuration helps shorten the representation of electrons by showing the elemental symbol of the noble gas in the prior row, and then the configuration of the rest of the electrons. In order to do this, you need to know the blocks of sub-levels on the periodic table:


First, you could find the electron configuration of an element, and identify which configuration has the same position as the noble gas prior to that element. You would then write that noble gas in brackets, and include the configurations after.
OR…
If we configure Phosphorous, we would take the noble gas from the previous row [Ne], and then use its place on the periodic table to write the configurations for the rest of the electrons. It is the third element down(represents energy level). Due to how it is all the way in the p block, we will need to first go through the s and d blocks. To do this, we take its energy level and use the maximum number for the row placement for both blocks → 3s^2, 2d^10. Since 2d^10 does not exist on the periodic table, we only use 3s^2. Lastly, we find its place in the P block which is where potassium is and get its configuration: 3p^3.
Lastly, we put this all together.
Noble gas→ [Ne] 3s² 3p³ <--superscript 3: 3rd element on row of P block
↑
The threes are there because it is the 3rd element down
Important note: An exception is that in the d block, you need to subtract an energy level from its configuration because it starts on the fourth row. This is because they require more energy to fill up.
Example: Technetium has the noble gas configuration of [Kr] 5s^2 4d^5, instead of [Kr] 5s^2 5d^5 because of this rule.
 Knowt
Knowt
