ECMT1020_Lecture_Week_2-1

Continuous Random Variables

It has 2 main characteristics:

1. set of its possible values is uncountable e.g. 2.345

2. compute probability of a given interval by integrating a function called probability density function.

Probability of a single value of a continuous random variable is 0.

A probability density function (PDF) of a continuous random variable is a function that describes the likelihood of the variable taking on a particular value. The PDF must satisfy two conditions:

1. The function is non-negative:

   

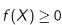
2. The total area under the curve of the PDF over its entire range is equal to 1:

   

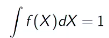
The probability that the variable falls within a certain interval can be found by integrating the PDF over that interval.

How to find probability using probability density function?

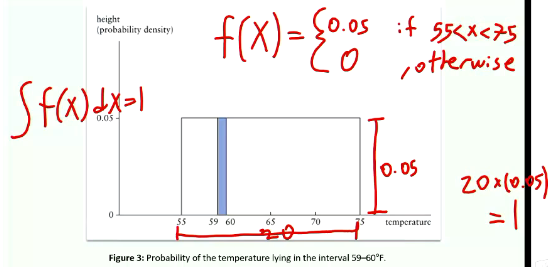
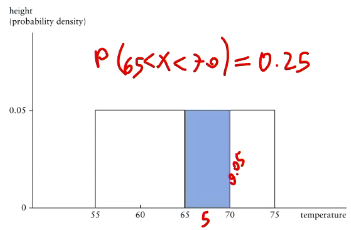
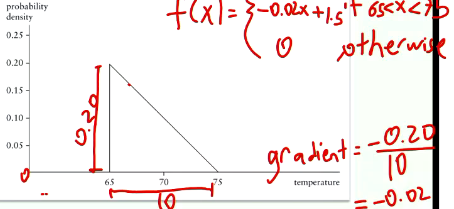
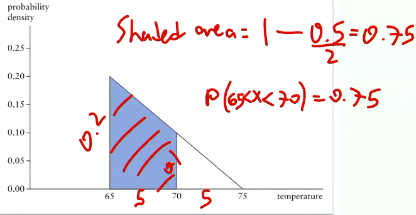
Expected value and variance of a continuous random variable

E(X) = ∫ x * f(x) dx, where f(x) is the probability density function.

the summation by integration of x with probability density function.

E[g(X)] = ∫ g(x) * f(x) dx, where f(x) is the probability density function of X and g(X) is a function.

Variance (σ²) = ∫ (x - μ)² * f(x) dx, where μ = E[X] and f(x) is the probability density function.

you can calculate standard deviation using the square root of variance.

Covariance

Covariance is a statistical measure that indicates the extent to which two random variables change together. It helps to determine the relationship between the variables: whether they tend to increase or decrease together.

Formula:

The covariance between two variables (X) and (Y) is calculated as:

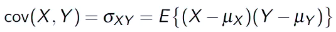
Where:

• (n) = number of data points

• (X_i) and (Y_i) = individual sample points

• (\bar{X}) and (\bar{Y}) = means of (X) and (Y) respectively.

Independence of random variables

Independence of Random Variables: Two random variables (X) and (Y) are independent if the occurrence of one does not affect the probability distribution of the other. Mathematically, this is expressed as:

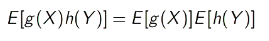
In particular, if X and Y are independent, E(XY) = E(X)E(Y)

Population Covariance: When two random variables are independent, their population covariance is zero: cov(X,Y) = 0

• because they don’t show any relationship (similar but not the same to correlation)

Cov(X, Y) = E[(X - μ_X)(Y - μ_Y)] = E[XY] - μ_Xμ_Y

Covariance rules

Here’s a concise table of covariance rules:

Where:

• X, Y, Z are random variables

• a, b are constants

Variance rules

Here’s a concise table for variance rules:

Correlation

Correlation is a statistical measure that describes the strength and direction of a relationship between two variables. It ranges from -1 to +1, where -1 indicates a perfect negative correlation, +1 indicates a perfect positive correlation, and 0 indicates no correlation.

Formula for Pearson correlation coefficient (r):

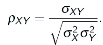
Where:

• ( n ) = number of pairs of scores

• ( x ) and ( y ) = variables being compared

What is the differences between covariance and correlation?

• Covariance:

  • Measures the degree to which two variables change together.

  • Can take any value from negative to positive infinity.

  • Indicates the direction of the relationship (positive or negative).

  • Formula: ( \text{Cov}(X, Y) = \frac{\sum (X_i - \bar{X})(Y_i - \bar{Y})}{n-1} )

• Correlation:

  • Standardized measure of the relationship between two variables.

  • Ranges from -1 to 1.

  • Indicates both the strength and direction of the relationship.

  • Formula: ( r = \frac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y} )

Key Difference: Correlation is a normalized version of covariance, making it easier to interpret.