Chapter 3: Forces and Newtons Laws of Motion

\

• From our discussion in Chapter 1 of frames of reference, you should be able to convince yourself that, if 2 objects have the same velocity, the relative velocity between them is zero and therefore one object looks as though it is at rest with respect to the other.
• An object that appears to be at rest in the Earth frame of reference will simply be stated to be “at rest” relative to us (the observers)

Forces

• An object does not change its velocity (accelerate) on its own. An interaction is required between that object and another object.
• This interaction can be direct as in the case of contact force, or it may take place via an action at a distance.
• If there is a net unbalanced force (the forces on an object do not add up to zero), then there will be an acceleration. If there is no change in speed or direction, the object is not accelerating, and the net force must be zero.
• Unless an object is in deep space, far from the influence of any other objects, objects experience a net force of zero because two or more forces are in opposition to each other, canceling out each other.
• Weight is the most common force and has its own formula.
• Weight is a vector force that depends on an object's location in the universe, while mass is a scalar measure of an object's inertia.
• The gravitational field strength (g) is the same as the acceleration due to gravity in free fall and projectile motion.
• Contact forces, such as a push, are not fundamental forces and are actually an overall effect that results from many different types of forces.
• Contact forces refer to all the forces in the table except for gravity and electricity.

Newtons Law of Motion:

The ability of an object to resist a change in its state of motion is called inertia. This concept is the key to Newton’s first law of motion.

• All forces, except for gravity, are electromagnetic and can be explained in terms of charges interacting with other charges.
• All daily life forces are either gravitational or electromagnetic, while the strong and weak nuclear forces round out the list of fundamental forces.
• An object is in a state of equilibrium when all forces acting on it produce no net change. Dynamic equilibrium refers to a moving object, while static equilibrium refers to a stationary object.
• Isaac Newton published his work, the Mathematical Principles of Natural Philosophy, in 1687, revolutionizing the rational study of mechanics by introducing mathematical principles that all of nature was considered to obey.

The acceleration produced by the force is in the same direction as the force. The second law is sometimes expressed as: = m. However, to preserve the vector nature of the forces, and the fact that by “force” we mean “net force,” we write the second law as:”

TIP:

Make sure you understand all of Newton's laws. On an AP free-response problem, you should make a declaration like F = O (for equilibrium) or F = ma (for accelerated systems).

\
Sample Problem

How much does a 2-kg mass weigh on the surface of Earth?

Solution

We use the formula for weight:

\

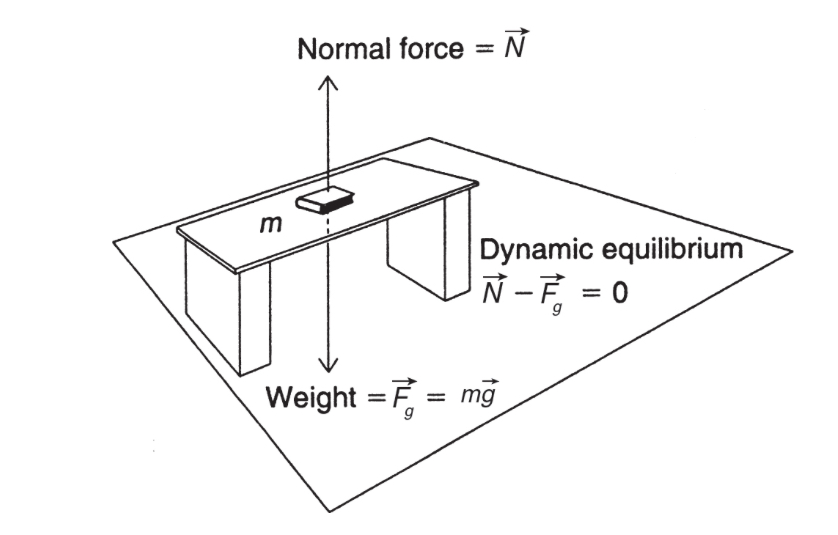
Free body diagrams

• Free body diagrams are a visual tool used to represent the forces acting on an object.
• These diagrams show the object as a dot and arrows to represent each force acting on it.

The direction and length of the arrows indicate the direction and relative magnitude of the force.

\
Example: An object has three forces pulling on it in the directions shown.

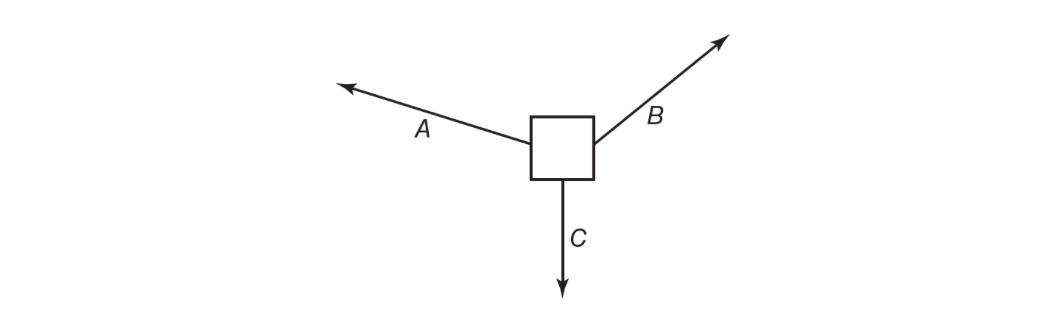
Choose your x- and v-axis based on the motion of the object. (One axis should be in the direction of acceleration!) Break vectors A and B into components using trigonometry. Then add up the x-components separately from the y-components.

\

• Centripetal force is the force that keeps an object moving in a circular path. It always points towards the center of the circle and is required to overcome the tendency of an object to move in a straight line.

• The magnitude of the centripetal force required to keep an object moving in a circular path depends on the object's mass, speed, and radius of the circle.

• The centripetal force is not a distinct type of force, but rather a resultant force that arises from other forces acting on the object in the circular path. For example, in the case of a car going around a curve, the centripetal force is the result of the friction force acting between the tires and the road.

• If the centripetal force acting on an object is not sufficient to keep it moving in a circular path, the object will move outwards, away from the center of the circle. This is known as centrifugal force, which is not actually a force but rather a perceived force resulting from an object's inertia.

• Examples of centripetal force in everyday life include the tension force acting on a swing as it moves back and forth, the gravitational force that keeps planets in orbit around the sun, and the force acting on a spinning top as it rotates.

  

Sample Problem

A car (mass M) takes a turn (of radius R) on a flat road without any slipping or sliding at a constant speed S. Find an expression for the minimum coefficient of friction needed between the wheels and road.

Solution

A rolling tire that is not slipping or sliding relies on static friction to accelerate the car. In this case, the required acceleration is a centripetal one (changing direction rather than speeding up or slowing down):

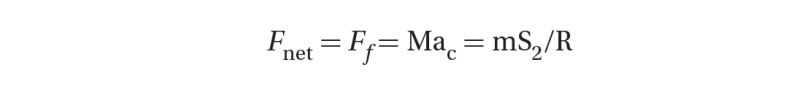
We can determine an expression for the minimum coefficient of static friction required to take this turn:

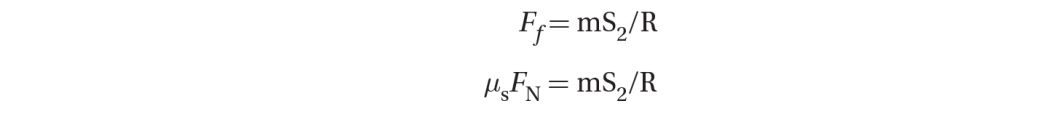
Since the normal force is only responsible for canceling the weight of the car in this case:

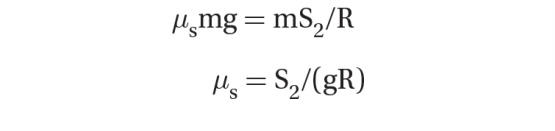
• Be careful about the changing roles of the forces in a vertical circular motion! Radially inward forces are positive and outward ones are negative. Compare the expressions for net force (centripetal force) at the top and bottom of a roller coaster loop.

\