Moles of gas and solution

Key Vocabulary

• Species – molecule, atom, ion, or compound in an equation

• Mole – amount of substance, unit is mole (mol)

• Relative formula mass (Mr) – sum of atomic masses in a chemical formula

• Relative molecular mass (Mr) – formula mass used for molecules

• Concentration – amount of solute in a solution, usually in mol/dm³ or M

• Solute – substance dissolved in a solvent

• Solvent – liquid in which a substance dissolves

• Solution – mixture of solute and solvent

• Decimetre cubed (dm³) – unit of volume, 1 dm³ = 1 litre = 1000 cm³

• Molar volume of a gas – volume occupied by one mole of gas

Moles of Gases

• Moles of a gas can be related to its volume, similar to solids and masses.

• 1 mole of gas occupies 24 dm³ (24,000 cm³) at room temperature and pressure (r.t.p, 25°C/298 K, 1 atm).

• The gas identity does not affect this; 1 mole of any gas occupies the same volume.

Equation:

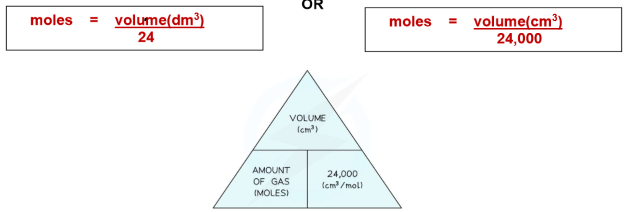
• Moles = Volume (dm³) ÷ 24

• Or, Moles = Volume (cm³) ÷ 24,000

Examples:

1. Moles in 300 cm³ of oxygen gas:

• Moles = 300 ÷ 24,000 = 0.0125 mol

2. Volume of chlorine gas in 0.4 moles:

• Volume = 0.4 × 24 dm³ = 9.6 dm³

3. Volume occupied by 0.10 g of hydrogen at r.t.p:

• Moles of H₂ = mass ÷ Mr = 0.10 ÷ 2 = 0.05 mol

• Volume = 0.05 × 24 dm³ = 1.2 dm³

4. Mass of 12.00 dm³ of oxygen at r.t.p:

• Moles = 12 ÷ 24 = 0.5 mol

• Mass = moles × Mr = 0.5 × 32 = 16 g

Reactions Involving Gases

• Using the balanced equation, the volume of a gas can be calculated from the moles of another species.

Example:

• 2.00 g CaCO₃ reacts with excess HCl:

  • Equation: CaCO₃ + 2HCl → CaCl₂ + CO₂ + H₂O

Steps:

1. Calculate moles of CaCO₃:

   • moles = mass ÷ Mr = 2.00 ÷ 100 = 0.02 mol

2. Use stoichiometric ratio (CaCO₃:CO₂ = 1:1) to find moles of CO₂:

   • 0.02 mol CO₂ expected

3. Calculate volume of CO₂:

   • volume = moles × molar gas volume = 0.02 × 24 = 0.48 dm³ = 4.80 dm³

Using a table:

Percentage Yield:

• Actual volume collected = 4000 cm³ = 4.00 dm³

• Theoretical = 4.80 dm³

• % Yield = (actual ÷ theoretical) × 100 = (4.00 ÷ 4.80) × 100 = 83%

Gas Calculations Questions

Volume of O₂ to oxidise 0.4 g Mg

• Equation: 2Mg + O₂ → 2MgO

• Mr Mg = 24 g/mol

• Moles Mg = 0.4 ÷ 24 = 0.0167 mol

• Mole ratio Mg:O₂ = 2:1 → moles O₂ = 0.0167 ÷ 2 = 0.00835 mol

• Volume O₂ = 0.00835 × 24,000 cm³ = 200.4 cm³

Volume of CO₂ from 20 g CuCO₃

• Equation: CuCO₃ → CuO + CO₂

• Mr CuCO₃ = 123.5 g/mol

• Moles CuCO₃ = 20 ÷ 123.5 = 0.162 mol

• Mole ratio = 1:1 → moles CO₂ = 0.162 mol

• Volume CO₂ = 0.162 × 24 dm³ = 3.89 dm³

Volume of Cl₂ to form 27 g FeCl₃

• Equation: 2Fe + 3Cl₂ → 2FeCl₃

• Mr FeCl₃ = 162.5 g/mol

• Moles FeCl₃ = 27 ÷ 162.5 = 0.166 mol

• Mole ratio Cl₂:FeCl₃ = 3:2 → moles Cl₂ = 0.166 × (3/2) = 0.249 mol

• Volume Cl₂ = 0.249 × 24,000 cm³ = 5,976 cm³ ≈ 5.98 dm³

Volume of CO₂ from 25 cm³ C₂H₆

• Equation: C₂H₆ + 3½O₂ → 2CO₂ + 3H₂O

• Mr not needed for gas volume

• Moles C₂H₆ = 25 ÷ 24,000 = 0.0010417 mol

• Mole ratio C₂H₆:CO₂ = 1:2 → moles CO₂ = 0.0010417 × 2 = 0.002083 mol

• Volume CO₂ = 0.002083 × 24,000 cm³ = 50 cm³

Maximum volume of butane from 13.5 g C₄H₆ and 18 dm³ H₂

• Equation: C₄H₆ + 2H₂ → C₄H₁₀

• Mr C₄H₆ = 54 g/mol

• Moles C₄H₆ = 13.5 ÷ 54 = 0.25 mol

• Moles H₂ = 18 ÷ 24 = 0.75 mol

• Mole ratio C₄H₆:H₂ = 1:2 → 0.25 × 2 = 0.5 mol H₂ needed → H₂ in excess, C₄H₆ is limiting

• Moles C₄H₁₀ = 0.25 mol

• Volume C₄H₁₀ = 0.25 × 24 dm³ = 6 dm³

Gas Volume Calculations Using Avogadro’s Law

• Equal volumes of gases at the same temperature and pressure contain equal numbers of molecules and moles.

• Therefore, for gases, mole ratio = volume ratio.

Examples:

1. Volume of O₂ to oxidise 10 cm³ CH₄

• Equation: CH₄ + 2O₂ → CO₂ + 2H₂O

• Mole ratio CH₄:O₂ = 1:2 → Volume ratio = 10 : 20 cm³

• Answer: 20 cm³ O₂

2. Volume of CO₂ from 25 cm³ C₂H₆

• Equation: C₂H₆ + 3½O₂ → 2CO₂ + 3H₂O

• Mole ratio C₂H₆:CO₂ = 1:2 → Volume ratio = 25 : 50 cm³

• Answer: 50 cm³ CO₂

3. Volume of O₂ for 40 cm³ CO

• Equation: CO + ½O₂ → CO₂

• Mole ratio CO:O₂ = 1:½ → Volume ratio = 40 : 20 cm³

• Answer: 20 cm³ O₂

4. Hydrogenation of 100 cm³ C₄H₆

• Equation: C₄H₆ + 2H₂ → C₄H₁₀

• Mole ratio C₄H₆:H₂ = 1:2 → Volume H₂ = 100 × 2 = 200 cm³

• Volume of C₄H₁₀ produced = 100 cm³ (mole ratio 1:1)

5. Chlorination of 20 cm³ C₂H₆

• Equation: C₂H₆ + 6Cl₂ → 6HCl + C₂Cl₆

• Mole ratio C₂H₆:Cl₂ = 1:6 → Volume Cl₂ = 20 × 6 = 120 cm³

• Volume HCl produced = 20 × 6 = 120 cm³

Predicting the Volume of CO₂ Produced

• Equation: CaCO₃ + 2HCl → CaCl₂ + H₂O + CO₂

Method:

• 50 cm³ of 2 M HCl is measured into a conical flask (excess).

• 0.4 g CaCO₃ is weighed into a phial and placed in the flask.

• A bung with delivery tube is fitted to a gas syringe.

• Flask is tilted to mix reactants; volume of CO₂ collected is recorded.

• Experiment is repeated and average volume of CO₂ calculated.

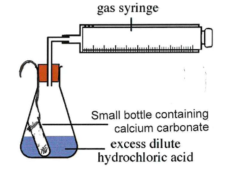
Calculations:

• Mr CaCO₃ = 100 g/mol

• Moles CaCO₃ = 0.4 ÷ 100 = 0.004 mol

• Mole ratio CaCO₃:CO₂ = 1:1 → moles CO₂ = 0.004 mol

• Volume of CO₂ at r.t.p = 0.004 × 24 dm³ = 0.096 dm³ = 96 cm³

Percentage yield:

• If actual CO₂ collected = 85 cm³,

• % Yield = (85 ÷ 96) × 100 ≈ 88.5%

Reason % yield < 100%:

• Gas may escape before collection.

• Some CaCO₃ may not fully react.

• Measurement inaccuracies in gas syringe.

Calculation of the Volume of H₂ Produced

• Equation: Mg + 2HCl → MgCl₂ + H₂

Method:

• 50 cm³ of 2 M HCl is added to a conical flask (excess).

• 0.04 g magnesium is placed in a phial in the flask.

• A bung with delivery tube is fitted; delivery tube end is in water trough.

• 100 cm³ measuring cylinder is filled with water and inverted over the tube.

• Flask is tilted to mix reactants; volume of H₂ collected by downward water displacement is recorded.

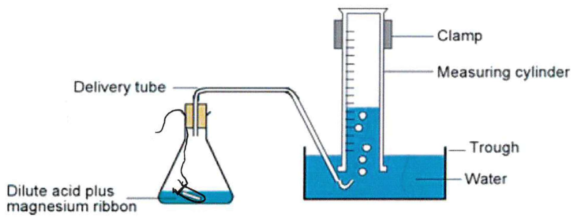
Calculations:

• Mr Mg = 24 g/mol

• Moles Mg = 0.04 ÷ 24 ≈ 0.00167 mol

• Mole ratio Mg:H₂ = 1:1 → moles H₂ = 0.00167 mol

• Volume of H₂ at r.t.p = 0.00167 × 24 dm³ ≈ 0.0401 dm³ = 40.1 cm³

Percentage yield:

• If actual H₂ collected = 36 cm³,

• % Yield = (36 ÷ 40.1) × 100 ≈ 89.8%

Reason % yield < 100%:

• Gas may escape during mixing.

• Magnesium may not fully react.

• Measurement errors in collecting gas.

Concentrations of Solutions

• Moles of solute can be related to solution volume and concentration.

• Concentration is measured in mol/dm³ or M (1 dm³ = 1000 cm³).

• A 1 M solution contains 1 mole of solute in 1 dm³ of solution.

Equations:

• Moles: n = c × V (V in dm³)

• Concentration: c = n ÷ V

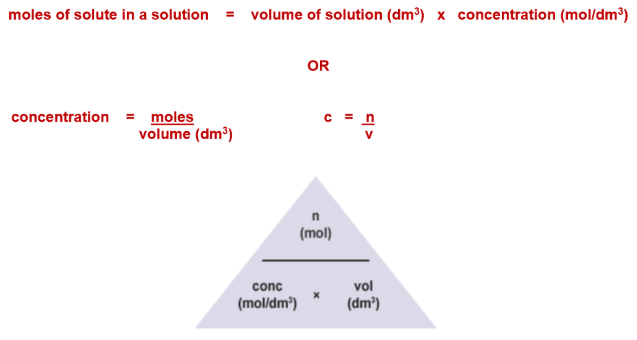
Examples:

1. Moles in 25 cm³ of 0.5 M NaOH:

• Convert volume: 25 ÷ 1000 = 0.025 dm³

• Moles = 0.025 × 0.5 = 0.0125 mol

2. Concentration of 50 cm³ containing 0.01 mol NH₃:

• Volume in dm³: 50 ÷ 1000 = 0.05 dm³

• Concentration: c = 0.01 ÷ 0.05 = 0.2 M

3. Concentration of 80 g NaOH in 800 cm³:

• Mr NaOH = 40 + 16 + 1 = 57 g/mol

• Moles NaOH = 80 ÷ 40 ≈ 2 mol (correct: 80 ÷ 40? Wait step by step)

  • Na = 23, O = 16, H = 1 → Mr = 23 + 16 + 1 = 40 g/mol

• Moles = 80 ÷ 40 = 2 mol

• Volume = 800 ÷ 1000 = 0.8 dm³

• Concentration = 2 ÷ 0.8 = 2.5 M

Moles of Solute in Solution

1. Moles of solute:

• Formula: n = c × V (V in dm³)

a. 50 cm³ of 2.00 M solution:

• V = 50 ÷ 1000 = 0.050 dm³

• n = 2 × 0.050 = 0.100 mol

b. 20 cm³ of 0.50 M solution:

• V = 20 ÷ 1000 = 0.020 dm³

• n = 0.50 × 0.020 = 0.010 mol

c. 20.0 cm³ of 0.10 M solution:

• V = 20 ÷ 1000 = 0.020 dm³

• n = 0.10 × 0.020 = 0.002 mol

2. Concentration of solution:

• Formula: c = n ÷ V (V in dm³)

a. 0.05 mol in 200 cm³:

• V = 200 ÷ 1000 = 0.200 dm³

• c = 0.05 ÷ 0.200 = 0.25 M

b. 0.003 mol in 25 cm³:

• V = 25 ÷ 1000 = 0.025 dm³

• c = 0.003 ÷ 0.025 = 0.12 M

c. 0.125 mol in 500 cm³:

• V = 500 ÷ 1000 = 0.500 dm³

• c = 0.125 ÷ 0.500 = 0.25 M

3. Volume of solution:

• Formula: V = n ÷ c (V in dm³, then convert to cm³)

a. 2.00 M solution containing 0.5 mol:

• V = 0.5 ÷ 2 = 0.25 dm³ = 250 cm³

b. 0.500 M solution containing 0.0300 mol:

• V = 0.0300 ÷ 0.500 = 0.06 dm³ = 60 cm³

4. Mass of solute:

• Formula: mass = n × Mr

a. 500 cm³ of 1 M NaOH:

• V = 500 ÷ 1000 = 0.5 dm³

• n = 1 × 0.5 = 0.5 mol

• mass = 0.5 × 40 = 20 g

b. 25.0 cm³ of 0.5 M NaOH:

• V = 25 ÷ 1000 = 0.025 dm³

• n = 0.5 × 0.025 = 0.0125 mol

• mass = 0.0125 × 40 = 0.50 g

5. Concentration of solution by mass:

a. 26.5 g Na2CO3 in 250 cm³:

• Mr Na2CO3 = 23×2 + 12 + 16×3 = 106 g/mol

• moles = 26.5 ÷ 106 ≈ 0.25 mol

• V = 250 ÷ 1000 = 0.25 dm³

• c = 0.25 ÷ 0.25 = 1.0 M

b. 62.5 g CuSO4·5H2O in 1 L:

• Mr CuSO4·5H2O = 63.5 + 32 + 16×4 + 5×18 = 63.5 + 32 + 64 + 90 = 249.5 g/mol

• moles = 62.5 ÷ 249.5 ≈ 0.25 mol

• V = 1 dm³

• c = 0.25 ÷ 1 = 0.25 M

6. Mass of AgNO3 for 50.0 cm³ of 0.2 M solution:

• V = 50 ÷ 1000 = 0.050 dm³

• n = 0.2 × 0.050 = 0.010 mol

• Mr AgNO3 = 108 + 14 + 16×3 = 108 + 14 + 48 = 170 g/mol

• mass = 0.010 × 170 = 1.70 g

Titration Calculations

• Titration involves reacting an acid with an alkali and measuring the exact volumes needed for neutralisation.

• If the concentration of one solution is known, the other can be calculated.

Example:

25 cm³ of 0.200 M NaOH required 40 cm³ of HCl to neutralise. Find the concentration of HCl.

Steps:

1. Balanced equation (underline reactants used):
   NaOH(aq) + HCl(aq) → NaCl(aq) + H2O(l)

2. Mole ratio:
   1 : 1

3. Volumes (dm³) and concentrations:

• NaOH: 25/1000 = 0.025 dm³, 0.200 M

• HCl: 40/1000 = 0.040 dm³, unknown

4. Moles of known substance (NaOH):

• n = V × c = 0.025 × 0.2 = 0.005 mol

5. Moles of HCl (from mole ratio 1:1):

• n = 0.005 mol

6. Concentration of HCl:

• c = n / V = 0.005 / 0.040 = 0.125 M

1. Calculate the concentration of potassium hydroxide solution used when 25cm³ was completely neutralised by 26.50cm³ of 0.10 moldm⁻³ hydrochloric acid?
KOH(aq) + HCl(aq) → KCl(aq) + H₂O(l)

Concentration of KOH: c = n / V = 0.00265 / 0.025 = 0.106 M

2. Calculate the concentration of sulfuric acid if 17.40cm³ was required to completely neutralise 25cm³ of a 0.50 moldm⁻³ potassium hydroxide solution.
2KOH(aq) + H₂SO₄(aq) → K₂SO₄(aq) + 2H₂O(l)

Concentration of H₂SO₄: c = n / V = 0.00625 / 0.0174 ≈ 0.359 M

3. In a titration, 10cm³ of a 1.0 moldm⁻³ solution of sulphuric acid was neutralised by 36.75cm³ of a sodium hydroxide solution. Calculate the concentration of the sodium hydroxide solution.
2NaOH(aq) + H₂SO₄(aq) → Na₂SO₄(aq) + 2H₂O(l)

Concentration of NaOH: c = n / V = 0.020 / 0.03675 ≈ 0.544 M

4. Calculate the concentration of hydrochloric acid when 16.85cm³ was required to completely neutralise 25cm³ of a 1.00 moldm⁻³ solution of sodium hydroxide.
NaOH(aq) + HCl(aq) → NaCl(aq) + H₂O(l)

Concentration of HCl: c = n / V = 0.025 / 0.01685 ≈ 1.48 M