MATHEMATICAL LANGUAGE AND SYMBOLS

The Importance of Mathematics Language

According to Schiro (1997), one very important element in a student’s mathematical success is his being able to %%communicate%% effectively in mathematics.

• Students should be given opportunities to correctly read, write, speak about and understand the math language in the classroom

• Discover the purpose for communicating mathematically with numerals or symbols

Parts of Speech in mathematics:

• Numbers

• Operations

• Relations

Characteristics of MATH LANGUAGE

The language of math would make it easy for the students to communicate their ideas among themselves:

• Precise – well defined and clearly stated, lacks ambiguity unlike ordinary language

• Concise – briefly stated

• Powerful – complex ideas are well expressed

• Nontemporal – No tenses (present, past or future)

Difference between Expressions and Sentences:

Expressions – combination of numbers or symbols or both (the noun given to a math object/does not make sense)

Sentences – state a complete thought  (have verbs)

SYNONYMS:  Mathematical objects have different names.  8,  5+3, 16/2, … 2^3

CONVENTIONS:  Conventions in math help you distinguish different types of mathematical expressions

The Grammar of Mathematical Language

Just like any ordinary language sentences of mathematics also have complicated structures which can be easily understood if one knows some of the basic terminologies of grammar in math.

Some parts of speech in math language are very similar to those in natural language and some are quite different.

Mathematical sentence: Two plus two equals four.

Natural Sentence:  Mary and Peter love Paris.

Three different meanings of “is”.

• 2 is a square root of 4.

• 2 is less than 5.

• 2 is a prime number.

FOUR BASIC CONCEPTS  Mathematical sentences can be written using the following:

• Sets

• Functions

• Relations

• Binary Operations

A Set is a collection of objects such as numbers or points.

Elements are members of the set.

symbol :    ϵ

2 ϵ P where P is a set of prime numbers

Set theoretic terms:

{(x,y): x^2 +y^2 = 1} represents a circle of radius 1

Function : one-to-one correspondence, dependent and independent variables

Functions can transform one mathematical object into another one.

EXAMPLES:

Square root of, 3 plus, two times

Sine, Tangent, logarithm

The derivative of sin(x) is cos(x)

d(sin(x))=cos(x)

Functions behave like nouns when used in mathematical sentences.

EX:   5 is less than 7

The square root of 25 is less than 7.

Functions can have properties that can be used conveniently in some mathematical sentences

Relation symbols behave like adjectives

Refers to a property rather than an object

Statement of relationship

EX: 2 is less than 5

Ex : “Equals” and “is an element of” are two other examples of relations

Binary operations act like a conjunction that sits between two objects (nouns)

EX  “two plus four”

Some familiar examples of binary operations are “plus”, “minus”, “times”, “divided by” and “raised to the”

Some ELEMENTARY LOGIC

PROPOSITION/STATEMENT

SYMBOLIC LOGIC

Symbolic logic studies relationships of natural language by using symbols.

Main ingredients are statements and connectives

SENTENCES

A statement is an assertion of something that can be either true or false.

The following sentences:

• It is sunny today;

• Ms. W. will have a broader audience next month;

• I did not join the club;

Not sentences:

• How’s the weather?  (questions)

• Cool! (interjections)

SIMPLE AND COMPOUND STATEMENTS

SIMPLE STATEMENTS

Simple statements do not contain other statements as their parts. We typically represent simple statements using letters P, Q, R, …; for example  (small letters are also used)

S:Your bicycle is slick;

C: I like its color.

COMPOUND STATEMENTS

These are combined statements with the use of connectives

…will be discussed thoroughly in Elementary logic

p        p is true (Assertion)

¬p       p is false (Negation)

Connectives and compound statements.

p∧q       p and q (Conjunction)    (note: connective “but” uses the same symbol)

p∨q       either p or q, or both(Disjunction)

p→q     if p then q (Conditional)

p ↔q   p if and only if q (Biconditional)

CONNECTIVES

Connectives join simple statements into more complex statements, called compound statements.

The most common connectives and their symbols are:

and/but ∧;  or ∨;

if …,then →.

Example. Your bicycle is slick and I like its color

S ∧ C.

The “operation” not ¬ turns a single statement into its negation and it is not a connective.

The symbols representing statements, connectives, and the negation operation form our dictionary. Parentheses are used for punctuation.

Note:

The connective or, in logic, has an inclusive meaning.

For example, Bob will play tennis or go to the movies is interpreted as follows:

Bob will either play tennis, or go to the movies, or do both.

The connective but has an identical role as the connective and, thus the same symbol ∧ is used for both.

For example, Your bicycle is slick, but I don’t like its color is written symbolically as  b ∧ ¬ c.

Parenthesis

If I do a web search for pages containing the terms “termites” or “cattle”, then I will search for pages containing “global warming”.

t:  I search for pages containing “termites;”

c: I search for pages containing “cattle;”

g: I search for pages containing “global warming.”

The symbolic form of the compound statement is then (t ∨ c)→g.

Note. The compound statement

t ∨ c → g, could be read as:

I search for pages containing “termites” or if I search for pages containing “cattle”, then I search for those containing “global warming”.

Truth table

Every logical statement, simple or compound, is either true or false.

We say that the truth value of a statement is true (represented by the letter T or the numeral 1) when the statement is true,  and false (represented by the letter F or zero,0) when the statement is false.

Example. Statements p and q,  If p: I play the piano is false, and q: I study logic is true,

then the conjunction p∧q ( p and q): I play the piano and study logic is a false statement.

A truth table summarizes all possible truth values of a statement.

For example, p can only either be true (T) or false (F), so its truth table (the simplest of all) is:

p       T          F

The next simplest truth table is the truth table for the negation, whose truth values are always the opposite as those of the original statement:

p    T     F

¬p    F    T

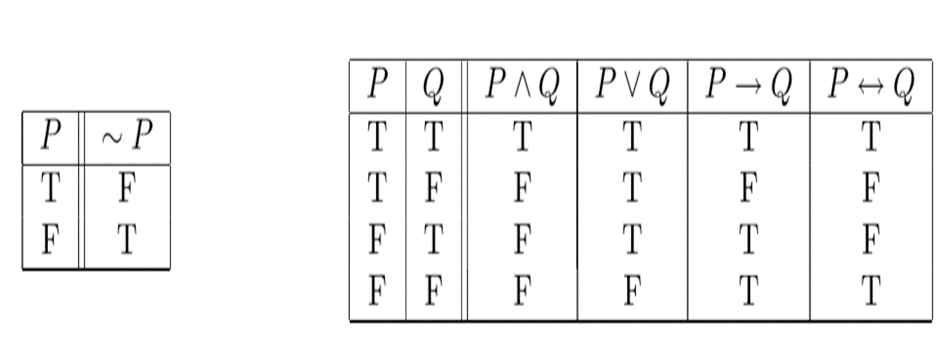
Construct the truth table for the compound statement ¬(p∨q)∧p.

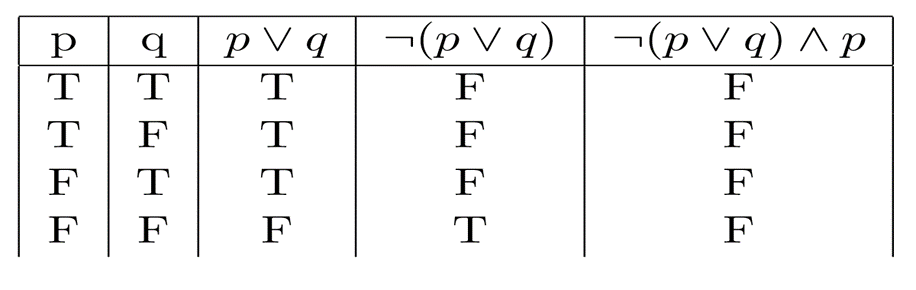
LOGICAL EQUIVALENCE

Two statements are logically equivalent when their truth tables are identical.

Any two statements of the form   p → q    and    (¬p) ∨ q  are logically equivalent.

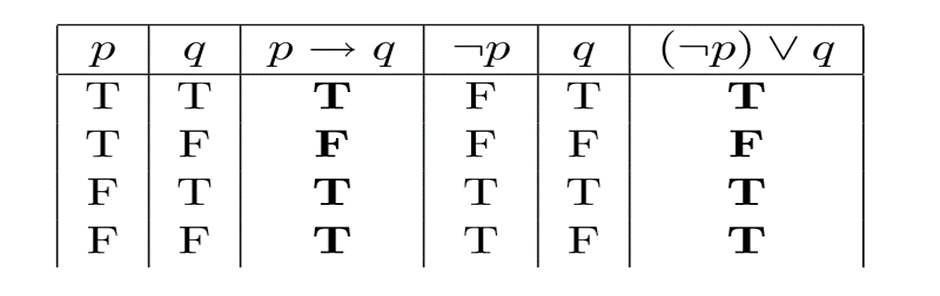
EXAMPLE:

The statements  “If the price is right, I will buy this”   and   “The price is not right or I will buy this”

have the same logical content.

De morgan’s laws

(A) ¬(p∧q) is logically equivalent to (¬p)∨¬q. (B) ¬(p∨q) is logically equivalent to (¬p)∧¬q.

EXAMPLE:  It is not true that: today is Wednesday and it is raining is equivalent to asserting that Today is not Wednesday or it is not raining.

Conditional Statement

For statements p and q, with p as antecedent/premise/hypothesis and q as the consequent/conclusion, the statements are as follows:  if p then q;  p implies q;  p only if q;  not p or q;  every p is q;  q, if p;  q provided that p;  q is a necessary condition for p;  q is a sufficient condition for p;  p yields q;  q follows from p

Exercise:  Write each of the following in “If p, then q” form.

a. The number is an even number provided that it is divisible by 2.

b. Today is Friday, only if yesterday was Thursday.

\n Bi-conditional

Bi-implication P ←→ Q is well-named as such since it is actually the same as

(P →Q )∧(Q → P).

In prose we can write “P is necessary and sufficient for Q,” for P ←→ Q, which is then the same as “Q is necessary and sufficient for P,” i.e., Q ←→ P.

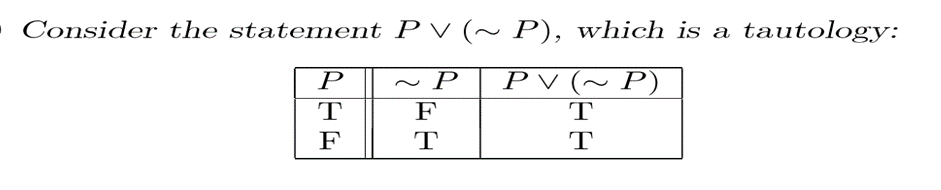
TAUTOLOGY

The statement is a tautology if the output in truth table contains entirely of T.

CONTRADICTION

The statement is a contradiction if the output in truth table contains entirely of F.

\n

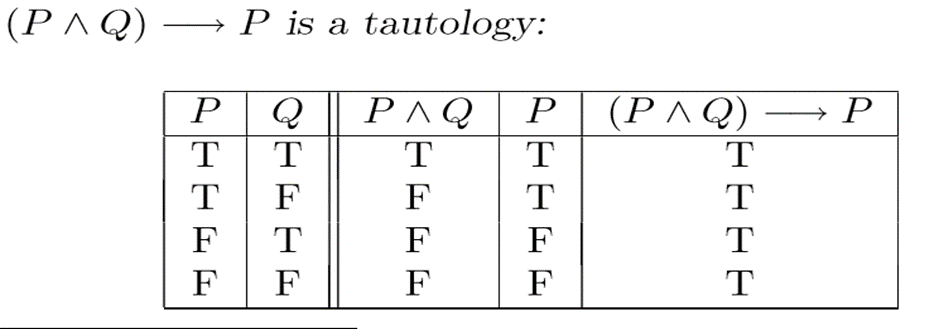
NEGATION

The negation ¬(p→q) is logically equivalent to the conjunction p∧¬q.

EXAMPLE:  My Lord, I reject your proposition that “If we lose the war, then our heads will fall”!

the negation of the statement:

“We lost the war, but our heads did not fall.”

CONVERSE, INVERSE, and CONTRAPOSITIVE

We begin with the statement  “If you stay, then I leave.”

The antecedent of this statement is   p:   you stay,

and the consequent is   q:   I leave.

The symbolic form of the conditional statement is then      p → q.

The converse statement is obtained by interchanging antecedent and consequent.

In symbols, the converse is simply     q →p.

Its English form is  “If I leave, then you stay.”

The inverse statement is obtained by negating the antecedent and the consequent.

In symbols, the inverse is    (¬p)→¬q.

Its English form is  “If you do not stay, then I do not leave.”

The contrapositive statement is one of the most important related conditionals (it will return in the study of validity of logical arguments).

It is obtained by both negating the antecedent and the consequent and by interchanging them.

In symbols, the contrapositive is    (¬q)→¬p.

Its English form is  “If I do not leave, then you do not stay.”

Exercise: Write the converse, inverse, and contrapositive of

a) “ If I get the job, then I will rent the apartment.”

b)  “Every parallelogram is a quadrilateral.”

QUANTIFIERS

The three quantifiers used by nearly every professional mathematician are as follow:

universal quantifier: ∀   read, “for all,” or “for every;” existential quantifier: ∃   read, “there exists;”

uniqueness quantifier: ∃!   read, “unique.”

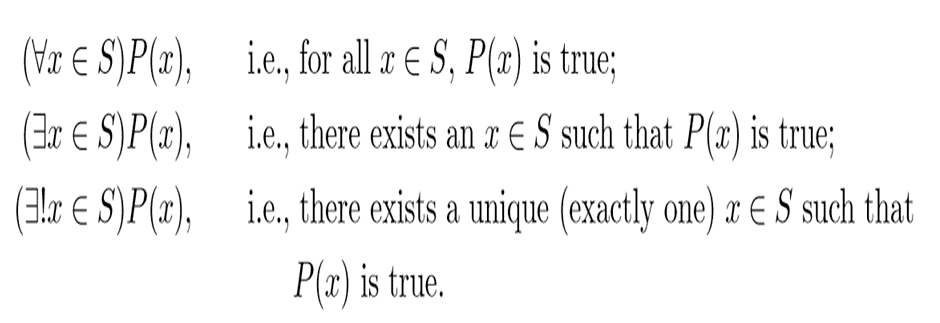
Here S is a set and P(x) is some statement about x. The meanings of these quickly become straightforward. For instance, consider

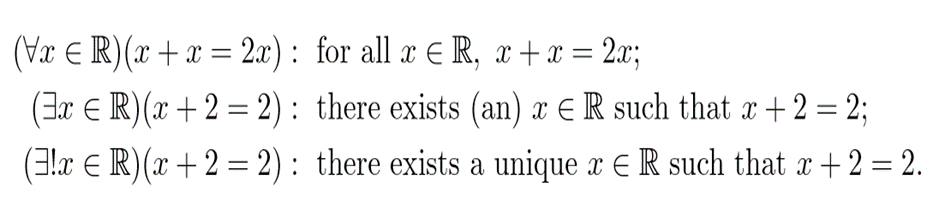
ELEMENTARY LOGIC

Propositions
Verbal or written assertions or statements, declarative sentences that are either true OR false BUT NOT both:
a) 2 + 5 = 9 (false) b) 5 is a prime number (true)
c) 3 is a prime number but 6 is not (true) d) a + b is divisible by 2 (neither T or F)
e) Every natural number can be written as the sum of the squares of three natural numbers. (true, Number Theory)
f) Every even number (an integer that is a multiple of 2) greater than 4 can be written as the sum of two prime numbers (true, law on numbers)
Notes: In a), the subject is “2 + 5” and the verb is “=” (“equals” or “is equal to”); b) the subject is 5 and the verb is “is”; c) compound sentence has 2 subject-verb pairs; d) has free variables, no truth value until specific values are substituted ( so that divisibility makes sense)
Letters P, Q, R, S, …, p, q, r, s, … are propositional variables as numbers stand for constants in algebra

Other Propositions:
4 + 3 = 7 (true, mathematical sentence)
The number 3 is positive and the number 2 is positive ( false, 2 is not negative)
25890134 + 1 is a prime number (either true or false but not both)
If a tree has n vertices, then it has n-1 edges (T or F)
2n + n is a prime number for infinitely many n
Every seven integer greater than 4 is the sum of two prime numbers ( T or F, Goldbach’s conjecture)
a + b = b + a for all a, b ԑ R (Proposition with word “for all”
2n = n 2 for some n ԑ N (Proposition with word “for some”
If the world is flat, then 3 + 3 = 6 ( paradoxical)

Propositional Calculus is the study of logical relationships between statements or propositions which are usually interpretable as meaningful assertions in real life contexts.

NOT Propositions/Statements: None can be given a Truth Value
Eat at the restaurant.
Mathematics is the best subject (an opinion, Ambiguous)
Your property or mine? (a question, a sentence but Not a statement)
Go directly to him. (a command, a sentence but NOT a statement)
Beautiful flowers! (an exclamation, a sentence but NOT a statement)
4 – x = 5 ( a declarative statement but NOT a statement, may be true or false only if a value for x is given
This is a false statement. (Ambiguous statement but there is specific reference for “This”)
a – b = b – a (symbols are not specified, may be true / false proposition depending on whether the symbols are “for all” or “for some” values.

Sentence MAY BE a statement but truth value cannot be ascertained because of ambiguity or lack of qualification.
Yesterday it was sunny. (meaning of sunny or its reference is unclear)
He thinks Manila is a wonderful city. (“thinks” denotes an opinion)
There is a number x such that x2 = 3. (may be true or false depending on value of x)
Mrs. Reyes is a brunette. (being a brunette is not qualified, lack of antecedence)
There will be moon tonight. (“will” denotes uncertainty, truth is determined in due time)

Paradox: truth value cannot be assigned. Example: “ I am lying to you”. Suppose the statement is true, I am lying, If I am lying, then the sentence is false. Suppose the sentence is false, then I am not lying and the statement is true.
Ambiguous Propositions:
Teachers are overpaid.
Farmers are poor.
It is hot in May in the Philippines.
Math is difficult.
Matrices are more interesting than graphs.
X2 = 0 implies x = 0 for all x. (set of all x not specified; would be true for all x ԑ R)

COMPOUND STATEMENTS
Combining statements/propositions to obtain compound propositions using standard connectives:
Connective Symbol Mathematical Term
NOT ₋ or ⌐ or ̴ negation
AND (but) ˄ conjunction
OR ˅ disjunction
IF … THEN … → conditional or implication
IF AND ONLY IF ↔ biconditional or material equivalence

Propositional variables or statements (p, q, r, s, …) can be combined by logical connectives (see table above) to obtain compound statements.
Example: p: Today is Monday; q: I will carry my umbrella in going out. (assertion)
̴p: Today is not Monday; ̴q: I will not carry my umbrella in going out (negation)
p ʌ q: Today is Monday and I will carry my umbrella in going out. (conjunction)
p ᴠ q: Today is Monday or I will carry my umbrella in going out. (disjunction)
p → q: Today is Monday then I will carry my umbrella in going out. (conditional)
q ↔ p: I will carry my umbrella in going out if and only if today is Monday (biconditional)

Truth Value of a Statement: truth or falsity of a statement ( T or F, 1 or 0)
Example: All cars are red False since there are cars that are not red.
All cars are not red, False since some cars are red
Three is an odd number and its square is nine. True (both statements are true)
Three is an even number or its square is nine. True (one of the statements is true)

Negation of Statements: Quantifiers
All cars are red. At least one car is not red.
Some of the cars are red. None of the cars is red.
None of the cars is red. At least one of the cars is red.

Arguments expressed in ordinary English can be written in the notation of mathematical logic and then studied. Consider the propositions and the argument:

p: It is not a good weather in the afternoon.
q: It is going to rain in the evening.
r: I should take my umbrella with me.

premise:
If it is not a good weather in the afternoon, then it is going to rain in the evening. p → q
If it is going to rain in the evening, I should take my umbrella with me. q → r

Therefore, If it is not a good weather in the afternoon, I should take my umbrella with me. conclusion: p → r

The conditional statement or implication p → q (if p … then q) can also be read as “p implies q”. p is the antecedent or hypothesis and q is the consequent or conclusion. As an exercise, give the other compound statements: converse, inverse and contrapositive. In such a case of p → q, p would be the premise and q would be the conclusion. (If it is not good weather in the afternoon, then it is going to rain in the evening)

Note that p → q being true does not imply that q → p is also true. Each statement or compound statement has its own truth value and these combinations, set as criteria, could be summarized in a truth table which would ultimately help determine the acceptability of the statements based on criteria that would help in decision making.

The Truth Table: A table giving the truth values of the compound statements in terms of their component parts.
Converting to Symbolic Logic Notation:

1. You win a prize of a new car or cash. p: You win a new car q: You win cash.
   Answer: p ᴠ q

2. If my mother does not come to get the dishes, my father will.
   p: My mother will get the dishes q: My father will get the dishes.
   Answer: p ᴠ q My mother or my father will get the dishes
   : ⌐p → q If my mother does not come to get the dishes, then my father will.

3. If I go and eat at the restaurant, I’m going to eat fish, but if I go to another restaurant, I’ll have steak.
   p: I am going to eat at the restaurant.
   q: I’m going to eat fish.
   r: I’ll have steak.
   Answer: (p ʌ q) ᴠ [(⌐p) ʌ r]

Converting to Mathematical Notation:

1.  If x is 3, then x squared is 9.                                 Answer:               (x = 3) → (x2 = 9)

2.  The cube of x is 27. It is necessary that x = 3.                 Answer:               (x = 3)  → (x3 = 27)

3.  if x squared is not 4, x is 2.                     Answer:               (x2 ≠ 4) → (x = 2) or ⌐ (x2 = 4)→ (x = 2)

Constructing the Truth Table

The truth values of a proposition built up from other propositions by using required connectives which are respectively determined by the truth values of the original propositions and way the proposition is built up from them.

The decision of accepting or rejecting a statement depends on the truth values of a proposition.  An acceptable statement is given a decision value or truth value of TRUE, T or 1; an unacceptable statement is given a decision value  of FALSE, F or 0.

The number of decision values (no. of rows in the table) would depend on the number of propositions n and notation 2n.  All criteria (propositions/compound statements) will each have the same number of decision values.

The truth table summarizes all decision values for propositions and compound propositions.  Whether a tautology or contradiction, the truth table aids in decision making.  Truth values are determined as follows and a sample table is presented.

Assertion and Negation:  proposition p and (⌐p) should not be true exactly when (⌐p) and p are true respectively, and vise-versa. p [or (⌐p)] may either be T or F.

Conjunction:  p ʌ q is T ONLY when BOTH statements are True.

Disjunction:  p ˅ q is T if AT LEAST ONE of the statements is True.

Conditional or Implication: p → q is F ONLY when p is True and q is False

Biconditional or Material Equivalence: p ↔ q  is T when BOTH p and q are True andZ when BOTH p and q are False.

Given:

p and q statements; n = 2;  2n = 22 = 4; 4 decision values

Given:  the Truth Table above

Find: Truth Values of the compound statements

use first truth value, p is T and q is T

a)    p ʌ ⌐q: p is T and (⌐q) is F; since T and F  is F then (p ʌ ⌐q) is F

b)  [(p ᴠ ⌐q) →(⌐p ʌ q)]: [(T ᴠ F) →(F ʌ T)]; [(T) → (F)]; since if T then F is F therefore,

[(p ᴠ ⌐q) →(⌐p ʌ q)] is F

c)  (p ʌ ⌐q) → [(p ᴠ ⌐q) →(⌐p ʌ q)]: (F) → [(F)]; since if F then F, therefore

(p ʌ ⌐q) → [(p ᴠ ⌐q) →(⌐p ʌ q)] is T

Given:  p, q and r, n = 3; 23 = 8, 8 decision values

Req’d:  form the truth table for (p → r) ᴠ [(p ʌ ⌐r) → (r ᴠ ⌐q)]

Tautology : when possible combinations of propositions that form the compound proposition are  all true

Contradiction : when possible combinations of propositions that form the compound proposition are  all false

Contingent : when possible combinations of propositions that form the compound proposition are neither all true nor all false (combination of T and F)

Self-Test:

Show that the following compound propositions are Tautology, Contradiction or Contingent:

a) p→p;  b) ⌐p ᴠ p;  c) [p ʌ (p → q)] → q;  d) (p → q) ↔ (q ᴠ ⌐p) are all tautology

e) p ʌ ⌐ p;  f) ⌐ (⌐p ᴠ p);  g) ⌐ { [ p ʌ (p → q) ] → q } are all contradiction

h)  p → [ ⌐p ↔ (p → q) ] is contingent

,