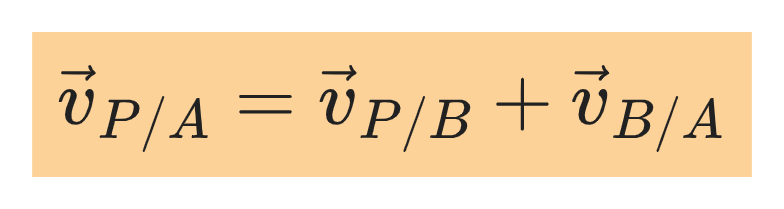Introduction

• In the previous chapter, the description of the motion of a particle could be done with a single coordinate.

• However, to understand the curved flight of a football, we need to extend our descriptions of motion to more than one dimension.

• This chapter focuses on motion in a plane that is motion in two dimensions although the same principles apply to three-dimensional motion.

• For motion in a plane, the vector quantities displacement, velocity, and acceleration now have two components and lie in a two-coordinate system rather than a one-coordinate system.

4.1 Velocity in a plane

• Before we can begin to describe motion of an object in a plane, we first need to be able describe its position, we do this using the position vector, r.

• The position vector, r of a point P in a plane is the displacement vector from the origin to P. It has components x and y.

  

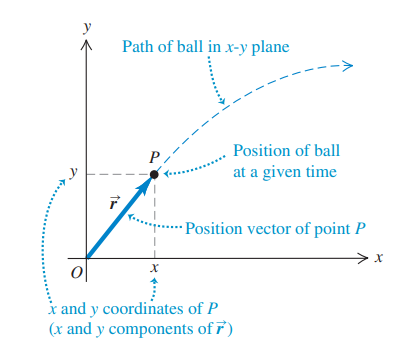
• The magnitude of the position vector, r of point P gives the distance of point P from the origin.

  

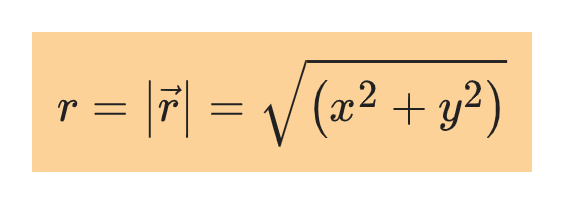
• The displacement, Δr of an object between two points P₁ and P₂ during the time interval, Δt = t₂-t₁ it takes to travel between the points is the change in the position vectors of the points.

  

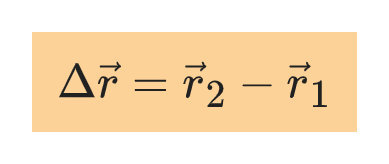
Definition of average velocity

The average velocity of a particle during a time interval Δt is the displacement Δr divided by Δt:

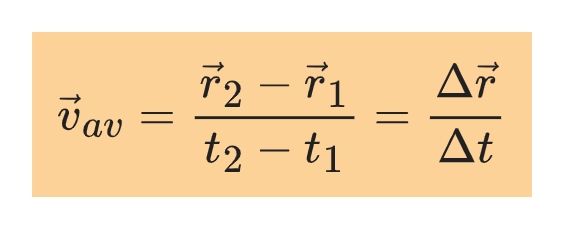
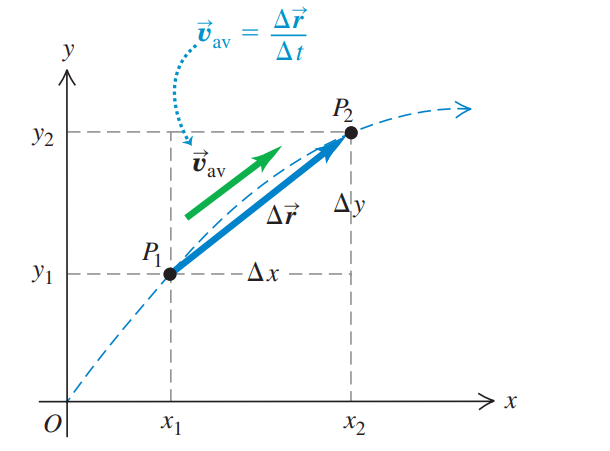
• NB: The average velocity is a vector quantity, and it has the same direction as Δr and a magnitude equal to the magnitude of the ratio of Δr to Δt.

  Regardless of the actual shape of the path taken by an object between the points P₁ and P₂, the magnitude of Δr is the straight-line distance from P₁ and P₂.

• The average velocity has components:

  

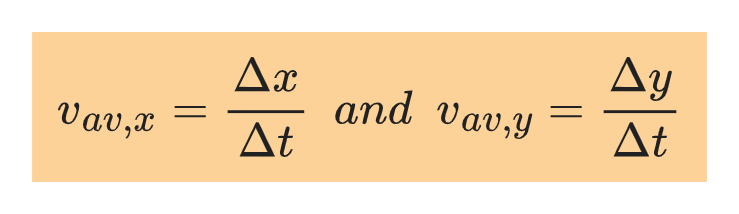
Definition of instantaneous velocity in a plane

The instantaneous velocity is the limit of the average velocity as the time interval Δt approaches zero:

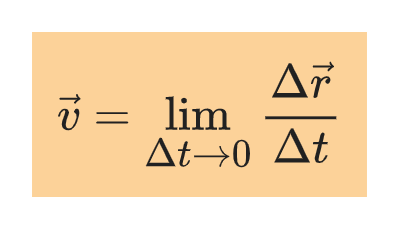
• The components of Δr are Δx and Δy, it follows that the components of the instantaneous velocity v are:

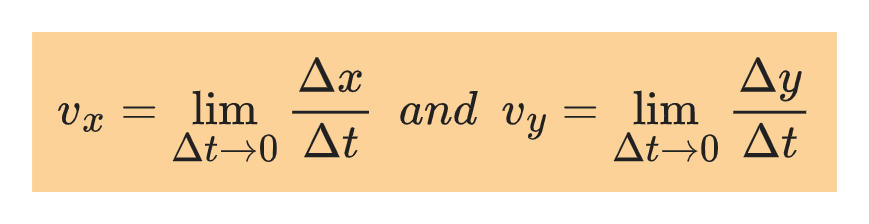
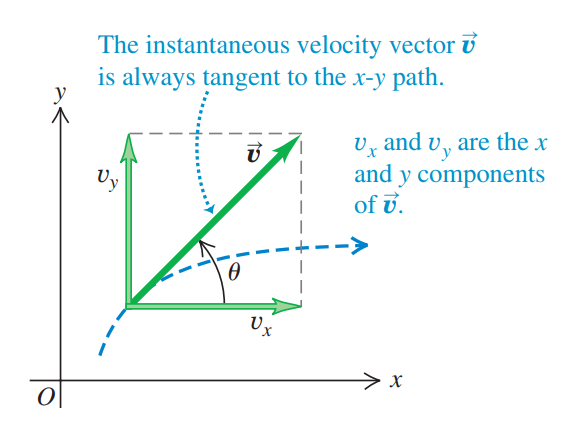
• The instantaneous speed of an object is the magnitude v of the instantaneous velocity vector v:

  

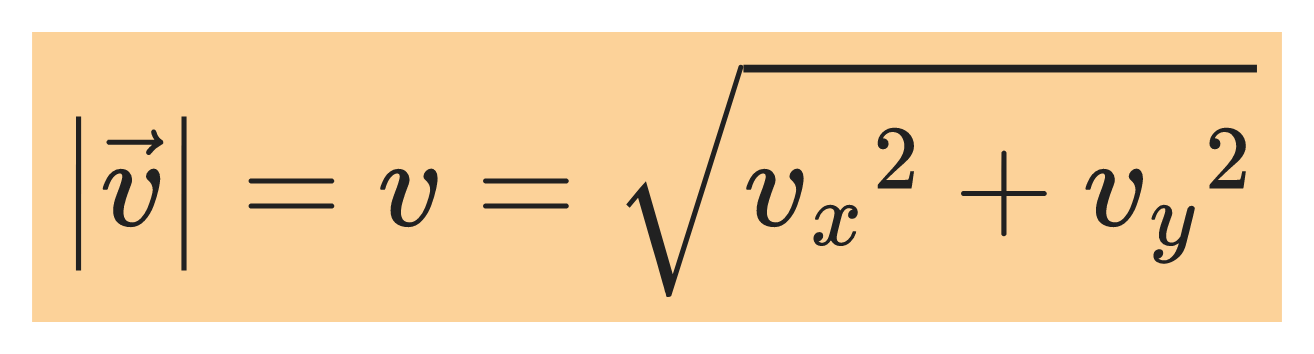
• The direction of v is given by the angle θ.

• When θ is measured counterclockwise from the +x axis,

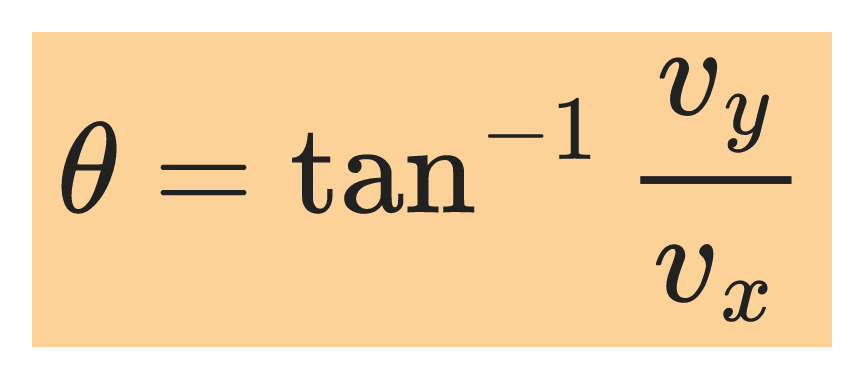
4.2 Acceleration in a Plane

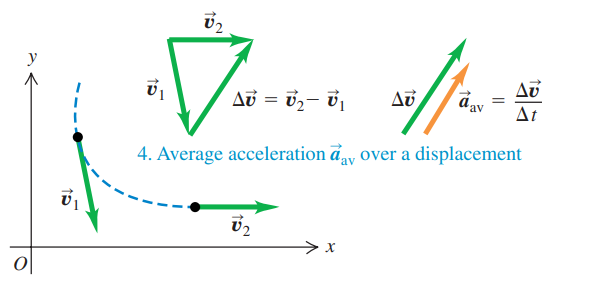
Definition of average acceleration

The average acceleration during a time interval Δt is the change in velocity, Δv divided by Δt:

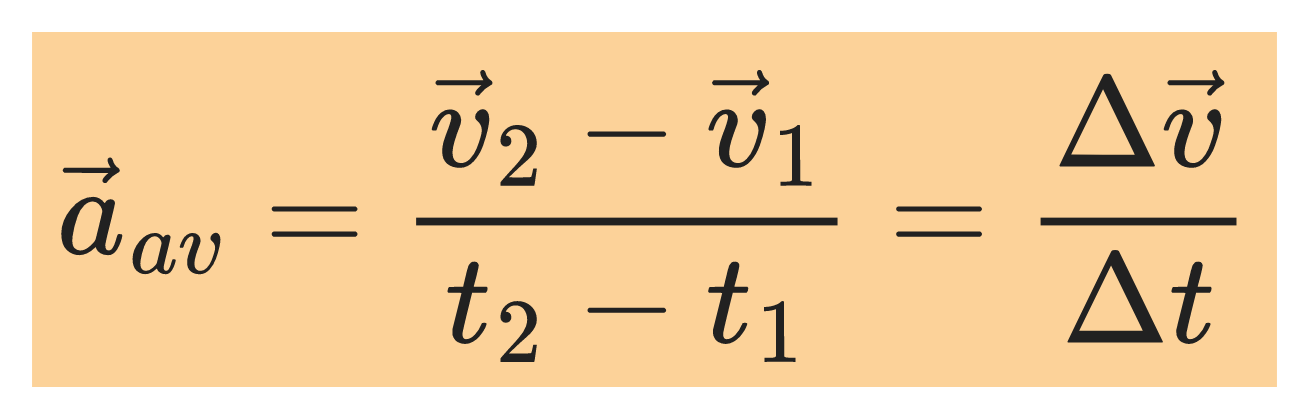
Definition of instantaneous acceleration

• When the velocity of a particle changes by an amount Δv as the particle undergoes a displacement Δr during a time interval Δt the instantaneous acceleration is the limit of the average acceleration as approaches Δt zero:

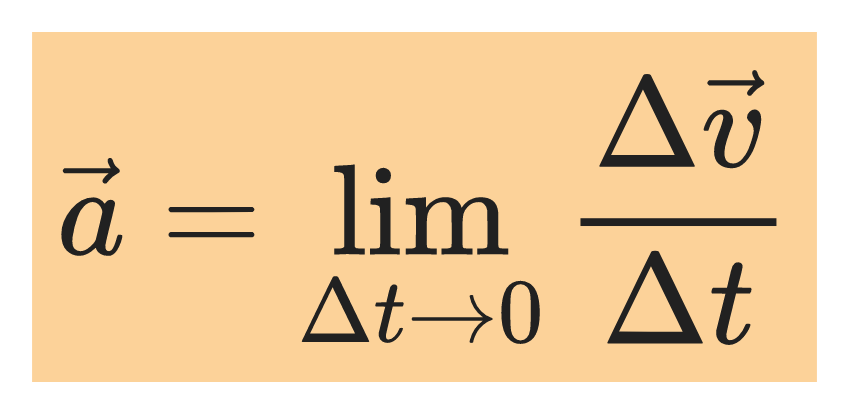
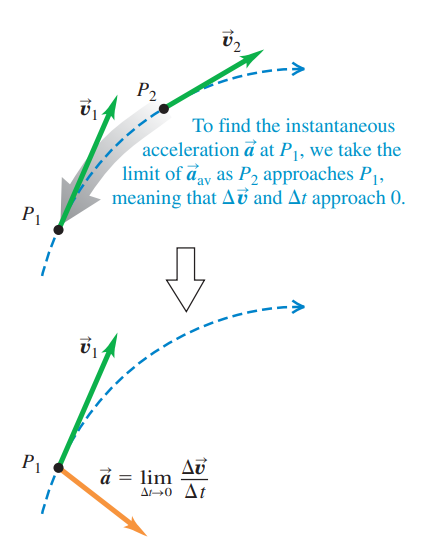
NB: The acceleration vector must always point toward the concave side of the curved path. Also, when a particle moves in a curved path, it always has nonzero acceleration, even when it moves with constant speed.

• The average acceleration has components:

  

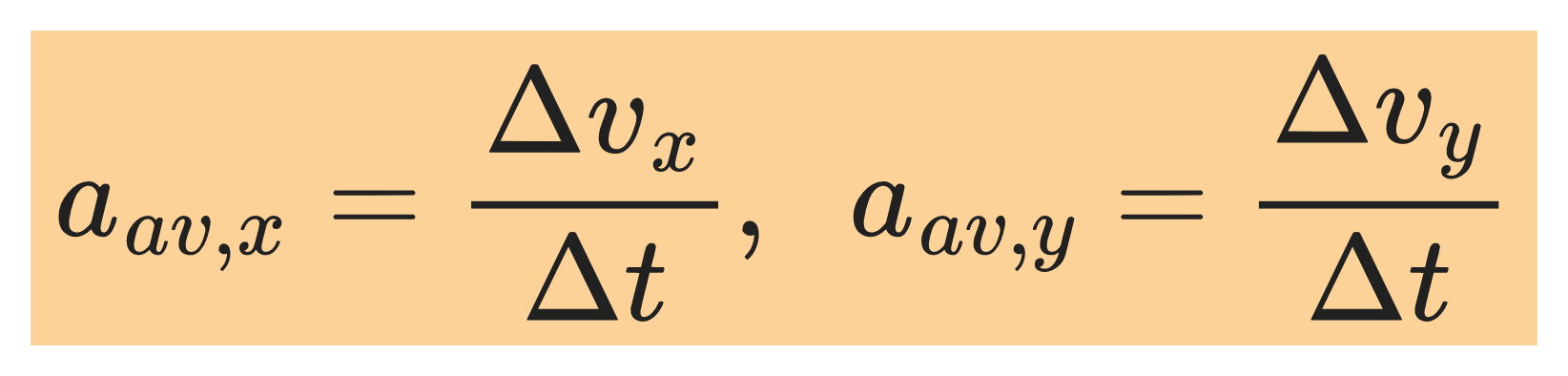
• Similarly, the instantaneous acceleration has components:

  

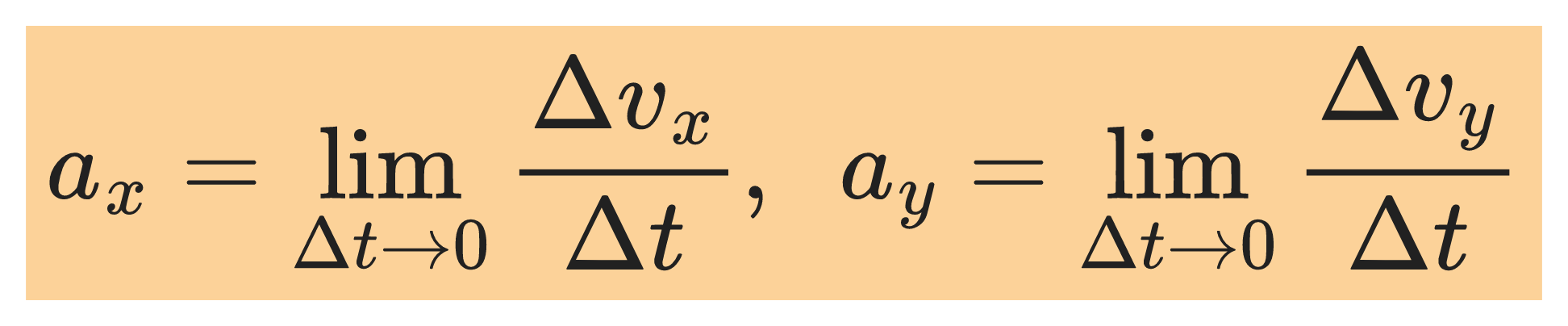
• The magnitude and direction of the acceleration vector are given by:

  

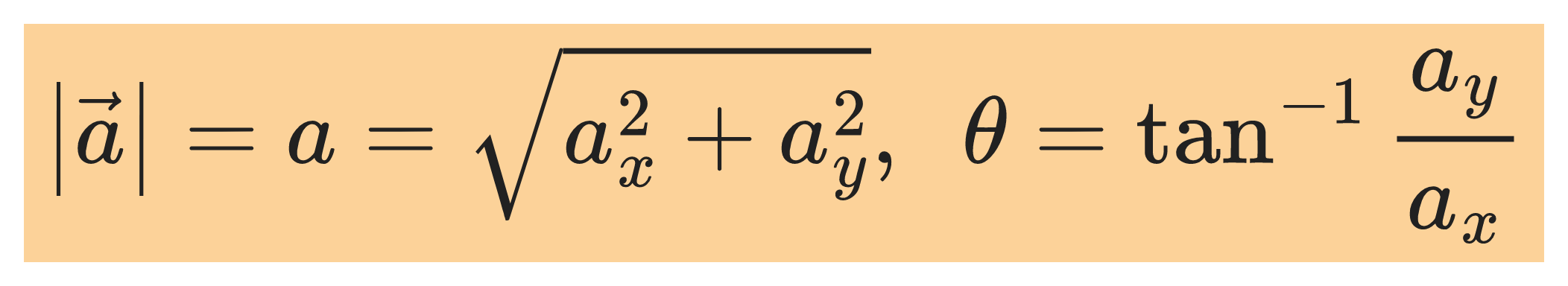
where θ is measured counterclockwise from the +x axis

Parallel and Perpendicular Components of Acceleration

• The components of acceleration can also be thought in terms of one component parallel to the object’s velocity, and one component perpendicular to the object’s velocity.

• The component of acceleration parallel to the velocity changes the speed of the object while the component of acceleration perpendicular to the velocity changes the object's direction of motion.

In general, a may have components both parallel and perpendicular to v.

4.3 Projectile Motion

• An object undergoes projectile motion when it is given an initial velocity and then follows a path determined entirely by the effect of a constant gravitational acceleration.

• The projectile’s vertical motion is independent of its horizontal motion allowing us to treat the x and y coordinates separately.

  

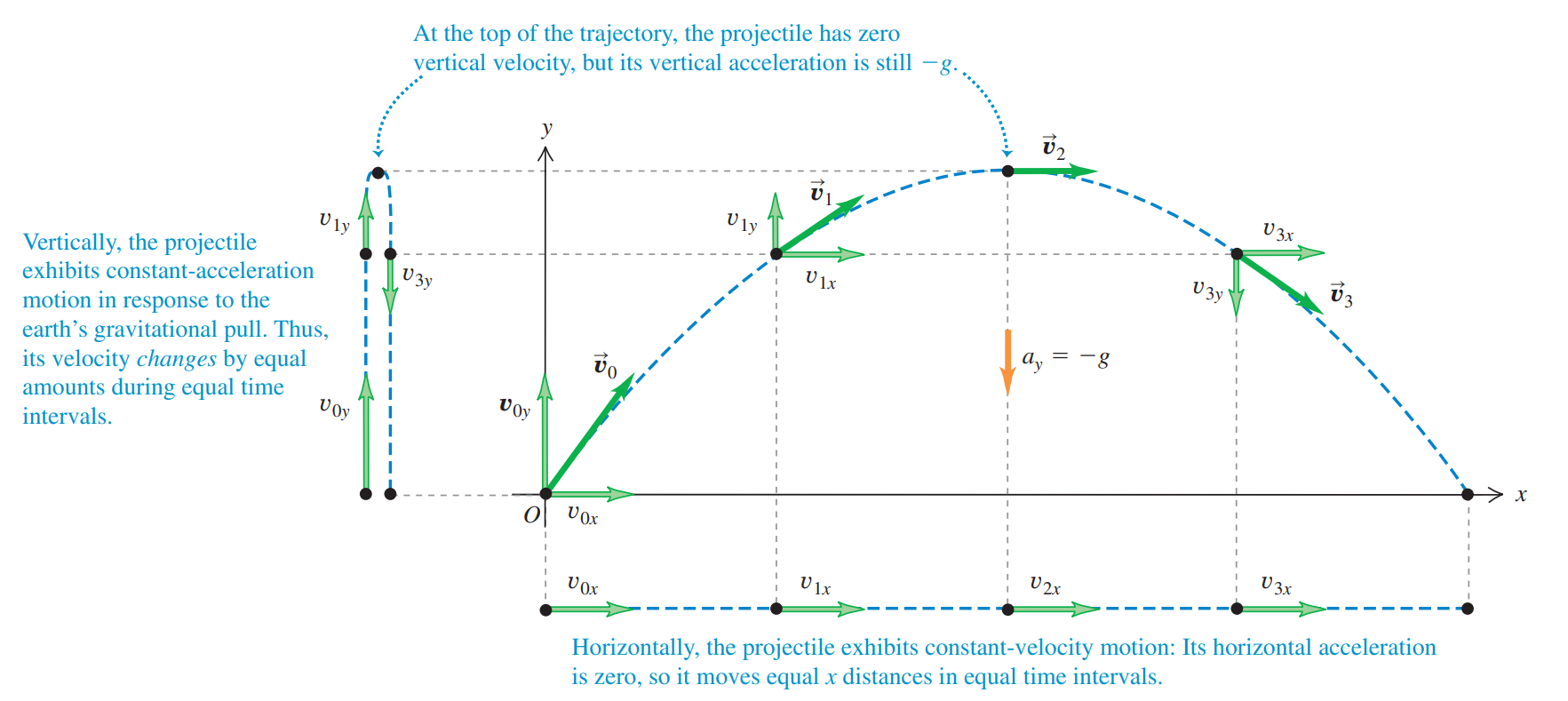
• It follows that the equations for uniformly accelerated motion can be used separately for each coordinate.

• In projectile motion, the horizontal acceleration is zero (acceleration due to gravity is purely vertical) and vertical acceleration is -g as shown.

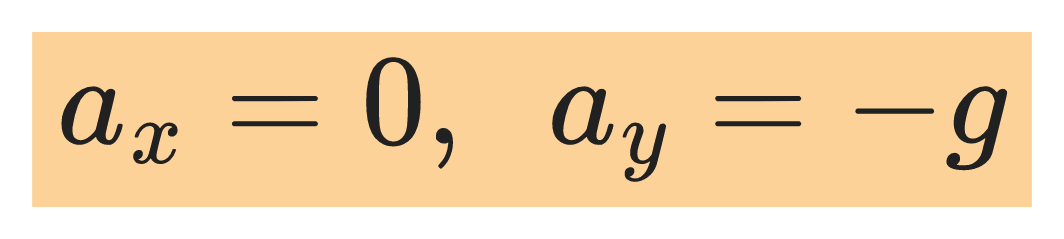
• Considering motion along the x-coordinate, we have the equations:

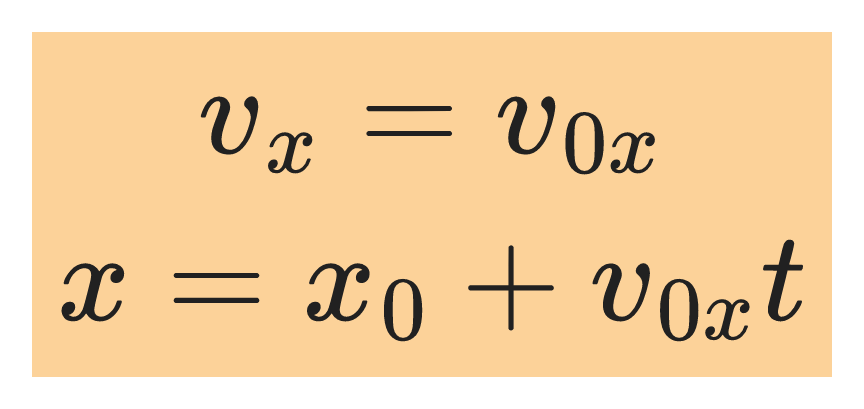
• For motion along the y-coordinate, we substitute y for x, vᵧ for vₓ, v₀ᵧ for v₀ₓ, and -g for a to get the equations:

  

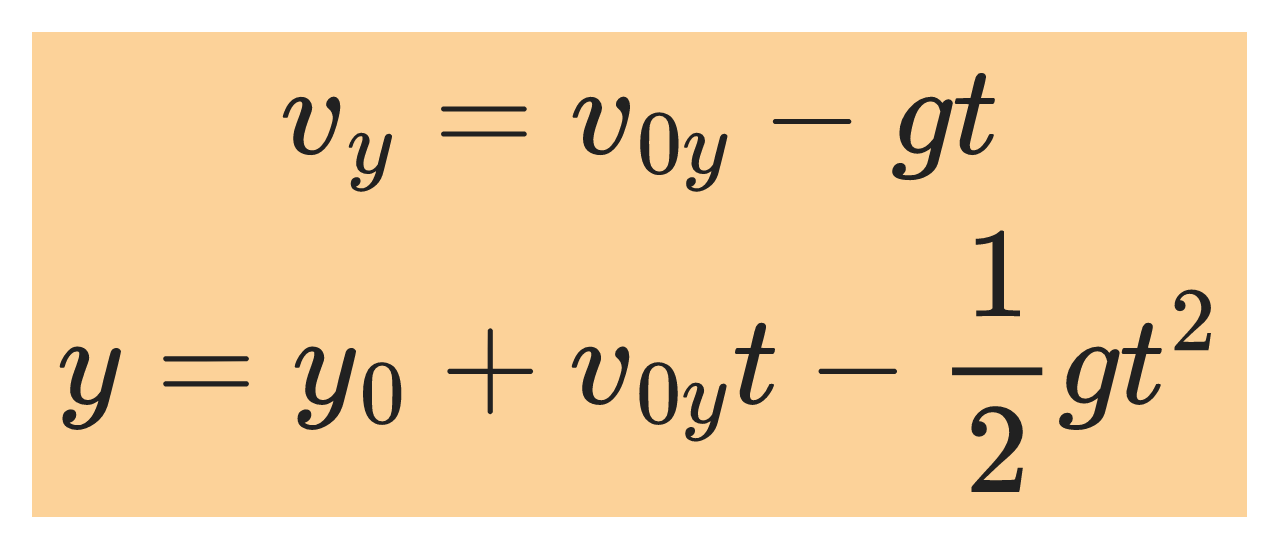
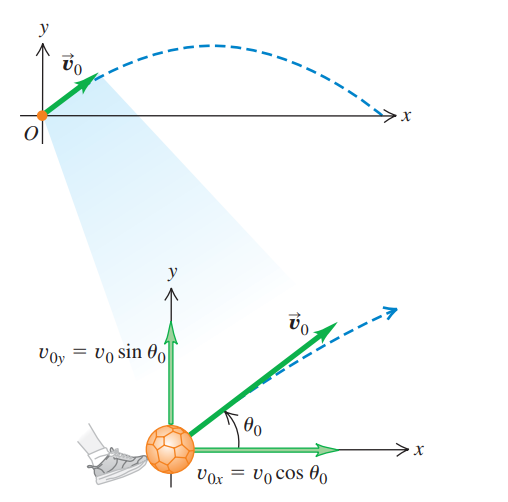
• v₀ₓ and v₀ᵧ are components of the initial velocity vector v₀ as shown:

• We know that:

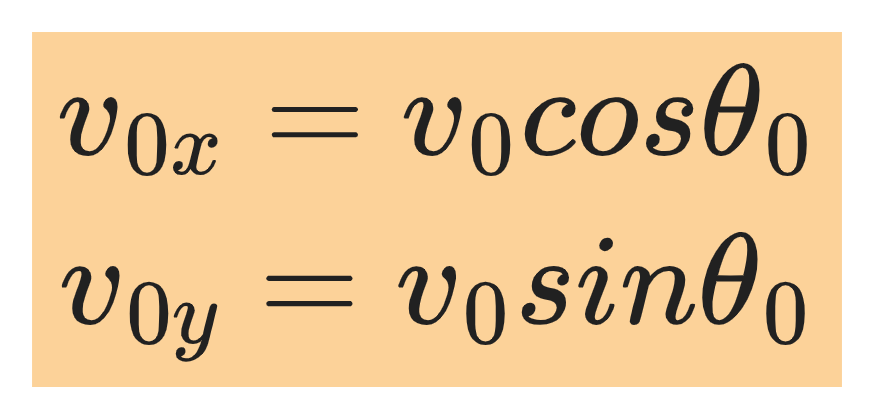
Also, if we take the initial position (at time t =0) as the origin then x₀ = y₀ = 0

• Then alternatively we have the following equations for projectile motion:

  

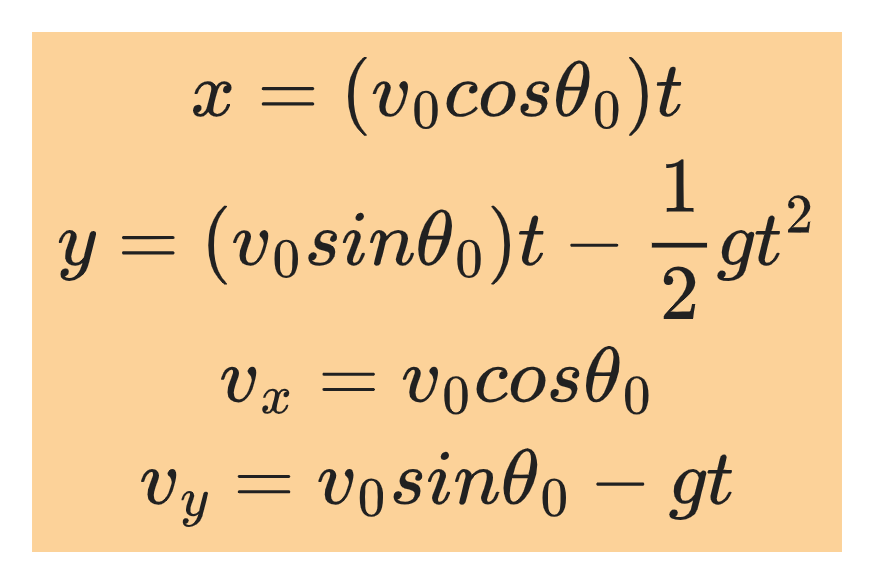
• The distance of the projectile from the origin is given by:

  

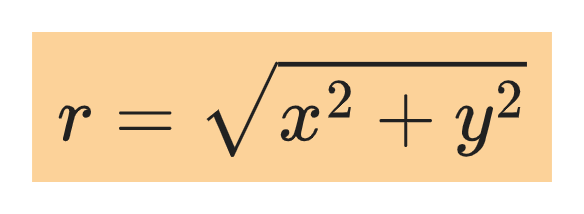
• The speed of the projectile by is given by:

  

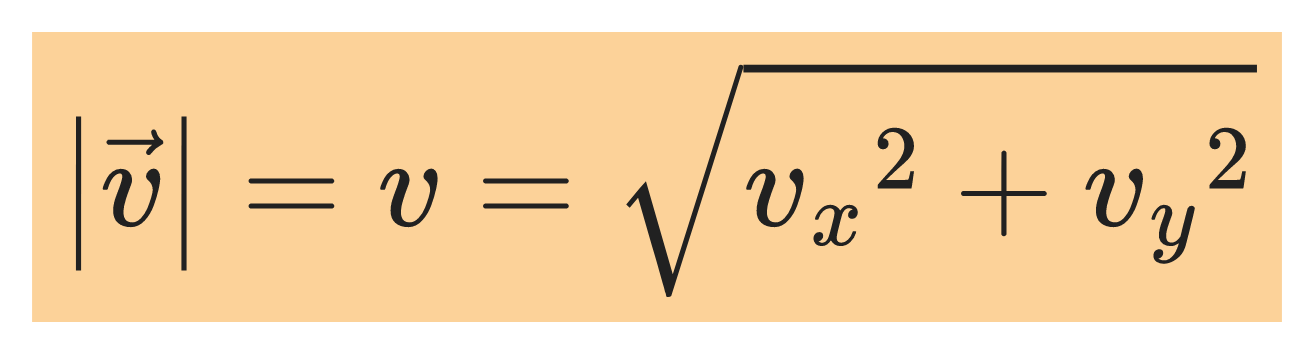
• The direction of the velocity is given by:

  

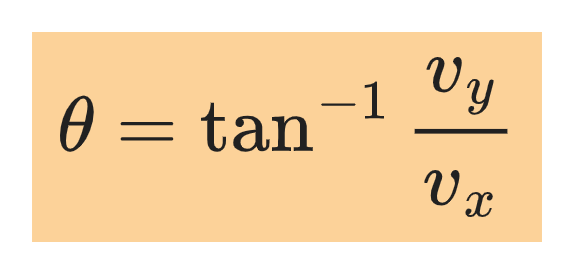
Shape of Path of a projectile

• The equations for projectile motion give the coordinates and velocity components of a projectile as functions of time.

• However, the shape of the path of a projectile is a graph of y as a function of t

• Using the equation of y as a function of t and the equation for x as function of t we can obtain an equation for y as a function of x as shown:

  

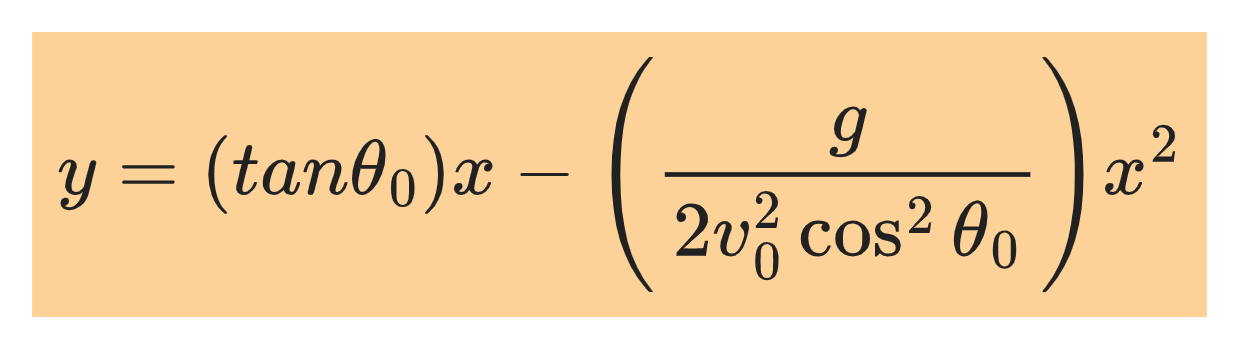
• The quantities v₀, tanθ₀, cosθ₀, and g are all constants, so the equation we have obtained is a relation between x and y, with general form:

  

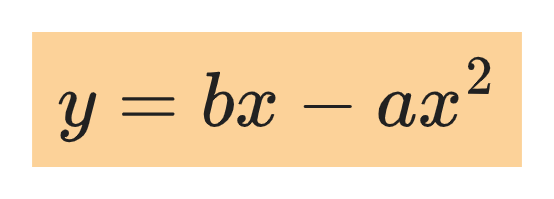
  This is the equation of a parabola. Therefore, for projectile motion the shape of the path of the projectile is a parabola.

Symmetry in Projectile Motion

• The path of a projectile is symmetric about the highest point. Thus, the time required to reach the highest point equals the time required to fall from there back to the initial elevation.

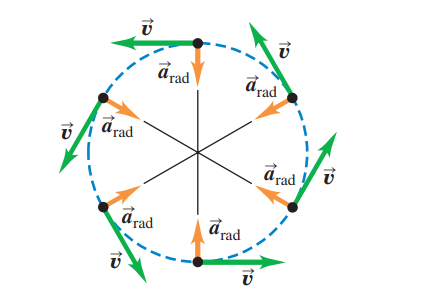
4.4 Uniform Circular Motion

• A particle moving in a circular path of radius R and constant speed v is said to move in uniform circular motion.

• Since a particle in uniform circular motion moves with constant speed there is no component of acceleration parallel (tangent) to the path.

• However, there is a perpendicular component of acceleration that changes the direction of velocity. It is related to the speed v of the particle and the radius R of the circle according to the following relation:

  

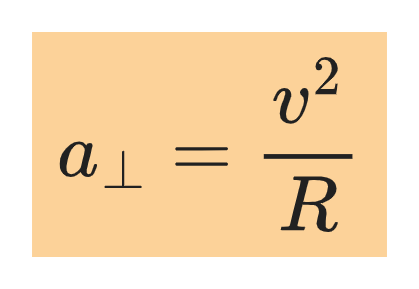
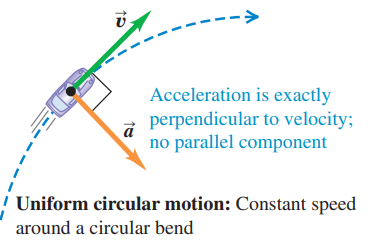
• The perpendicular component of acceleration is directed towards the center of the circle.

  

4.5 Relative Velocity in a Plane

• When a body P moves relative to a reference frame B, and B moves relative to a second reference frame A, the velocity of P relative to B is denoted by:

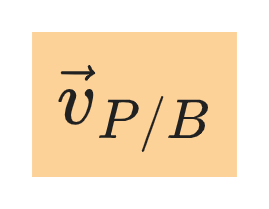
, the velocity of P relative to A is denoted by:

and the velocity of B relative to A is denoted by:

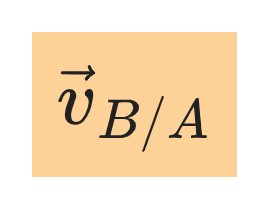
• These velocities are related by: