1.1: The Nature of Physics

• Physics predicts how nature will behave in one situation based on the results of experimental data obtained in another situation.

• Physics is based on hypothesis testing through experimentation and observation.

1.2: Units

• Physics experiments involve a variety of measurements. Measurement should be accurate and reproducible.

• Units of measurement:

1.3: The Role of Units in Problem Solving

• Conversion units help us switch from one unit to another.

• Examples:

  • Kilometers to meters

  • Grams to kilograms

  • Hours to seconds

• Standard prefixes used to denote multiples of ten:

  Prefix	Symbol	Factor
  tera	T	1012
  giga	G	109
  mega	M	106
  kilo	k	103
  hecto	h	102
  deka	da	101
  deci	d	10-1
  centi	c	10-2
  milli	m	10-3
  micro	\mu	10-6
  nano	n	10-9
  Pico	p	10-12
  femto	f	10-15

Reasoning Strategy: Converting between units

1. In all calculations, write down the units explicitly.

2. Treat all units as algebraic quantities. When identical units are divided, they are eliminated algebraically.

3. Use conversion factors in the text. Multiplying or dividing an equation by a factor of 1 does not altar the equation.

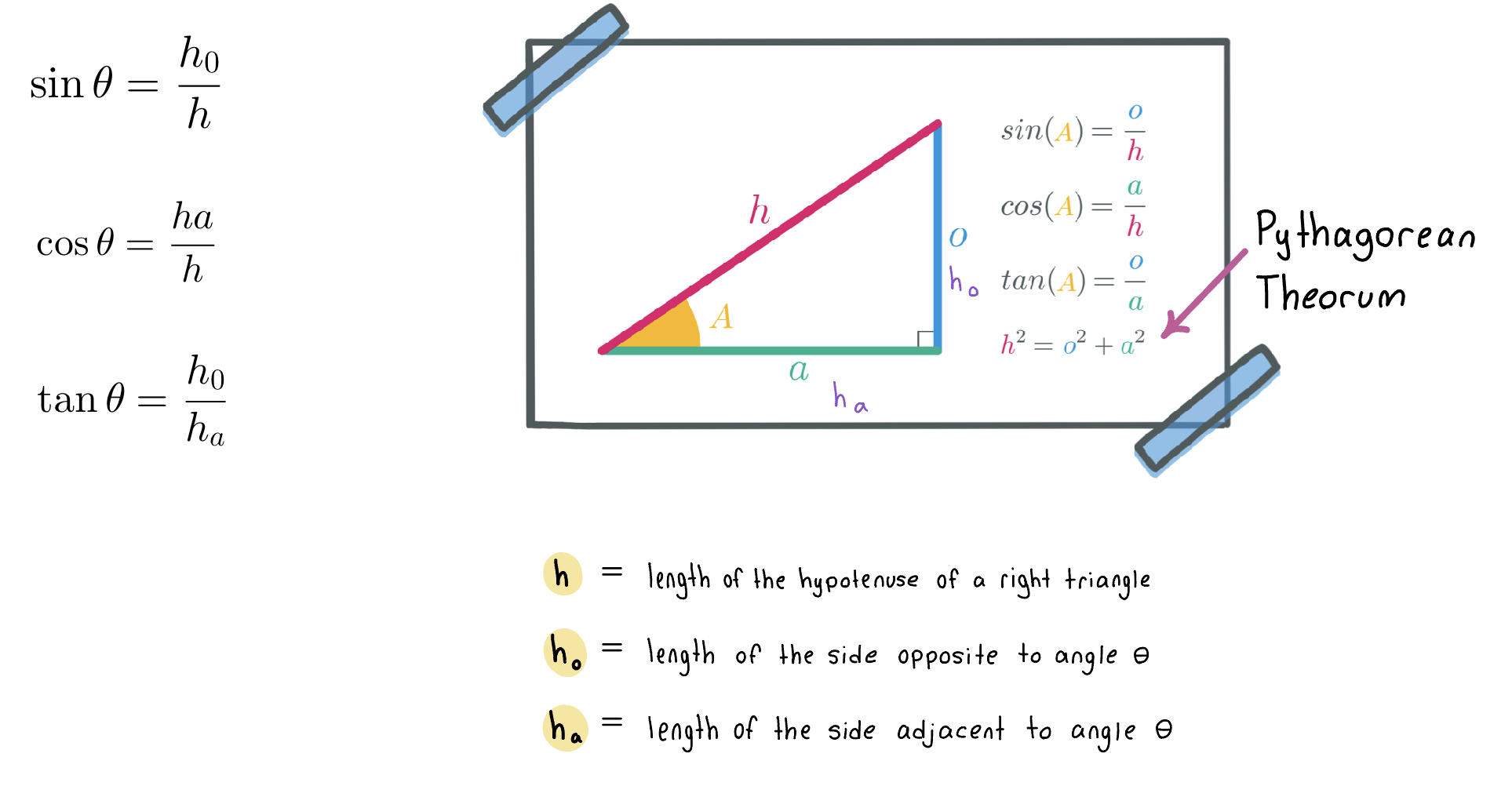
1.4: Trigonometry

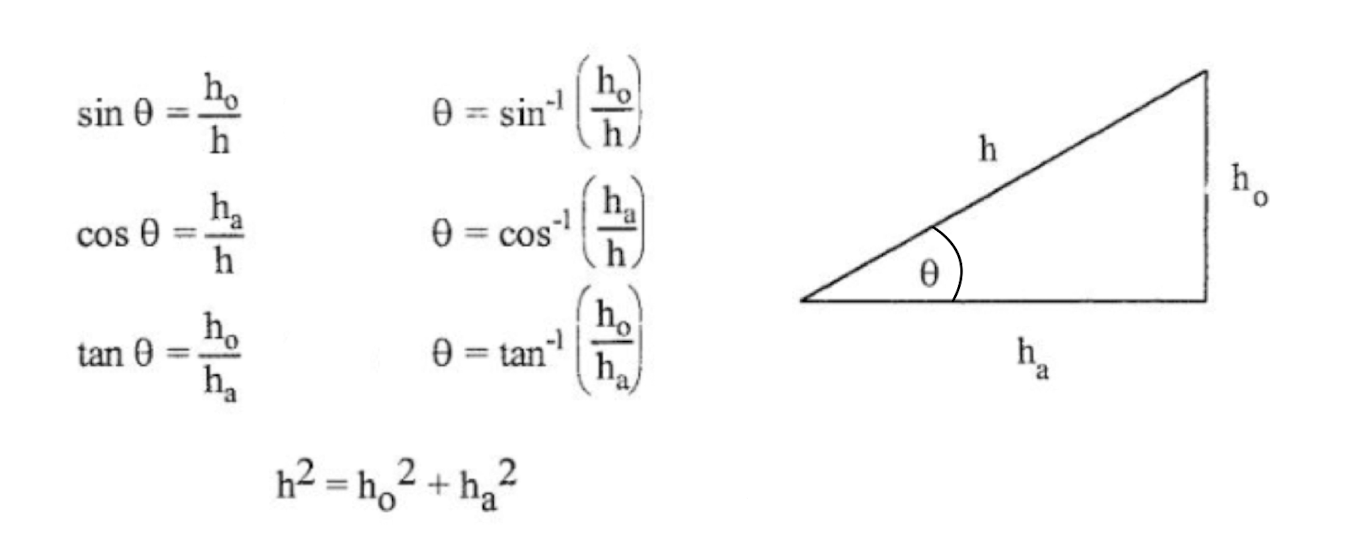h is the hypotenuse, but can also be referred to as the resultant, R.

• To find h, use the tangent equation.

1.5: Scalars and Vectors

• A scalar quantity is one that can be described by a single number.

  • It gives a measurement.

  • Examples: temperature, speed, mass

• A vector quantity deals with inherently with both magnitude and direction.

  • Examples: velocity, force, displacement

• Arrows are used to represent vectors. The direction of the arrow gives the direction of the vector.

• The length of a vector arrow is proportional to the magnitude of the vector.

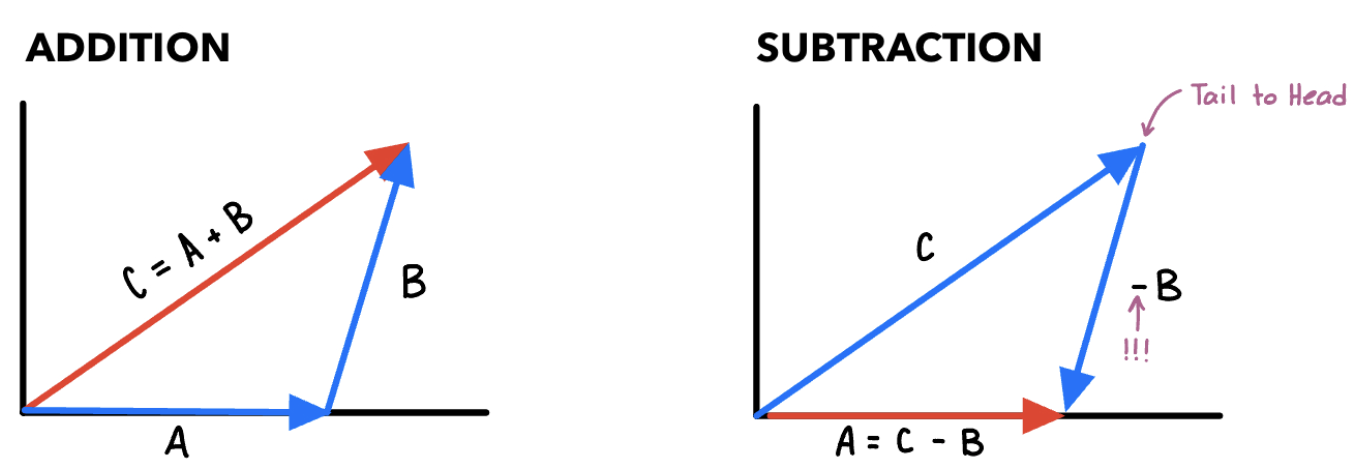
1.6: Vector Addition and Subtraction

• Often it is necessary to add one vector to another.

• “Resultant” = adding vectors together.

• Examples:

  You must consider the signs

  • Case 1: Signs are both positive.

    • (+3.0 u) + (+2.0 u) = +5.0 u

  • Case 2: A is positive and B is negative

    • (+3.0 u) + (-2.0 u) = +1.0 u

• Consider directions

1.7: The Components of a Vector

• x and y are called the x vector component and the y vector component of r.

• To find x, y, or r, you can apply the sine, cosine, and tangent equations.

1.8: Addition of Vectors by Means of Components

• Vectors can broken down into several parts.

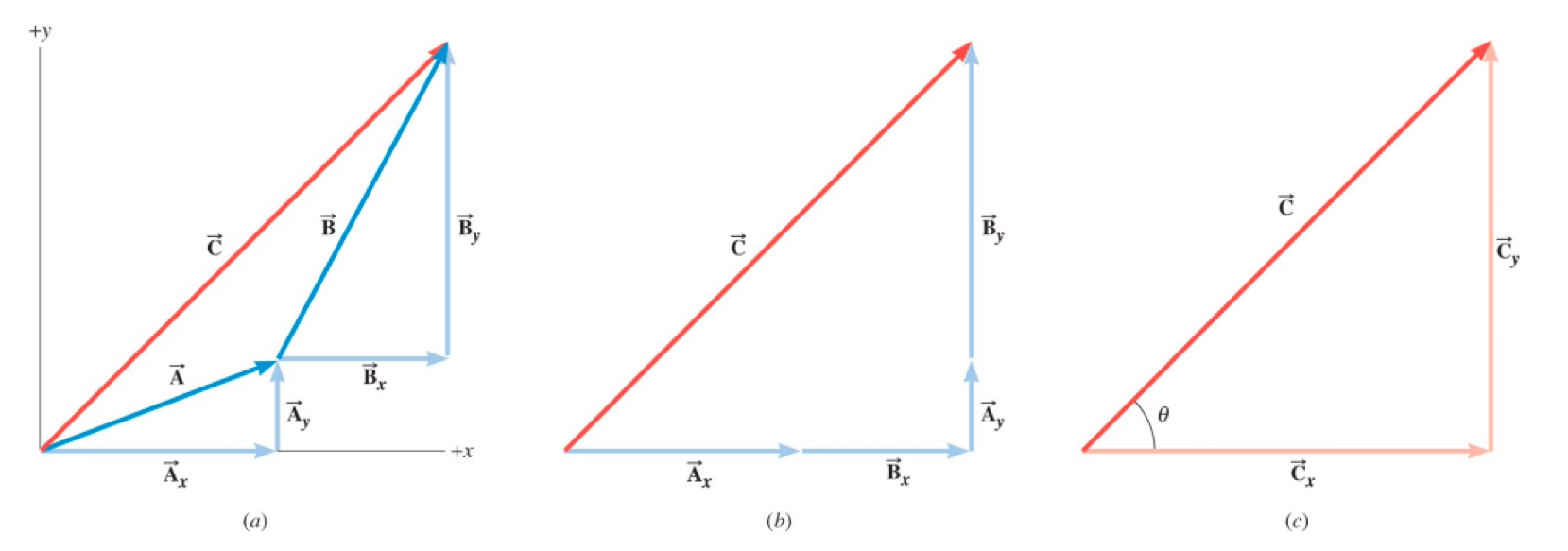There can be several x and y components.

Extra Notes

Main Idea:

• Physics is the branch of science that seeks to understand the fundamental principles governing the behavior of the universe.

  • It is based on hypothesis testing through experimentation and observation.

• Aims to describe and explain the interactions between matter, energy, space, and time.

• Based on the fundamental assumption that the laws of nature are consistent and can be described mathematically.

• The fundamental nature of physics lies in its pursuit of discovering the underlying principles and laws that govern the physical world.

• Seeks to uncover the fundamental building blocks of matter and the forces that act upon them.

• Physics encompasses a wide range of subfields, including:

  • Classical mechanics

  • Quantum mechanics

  • Electromagnetism

  • Thermodynamics

  • Relativity.

• The discoveries and advancements in physics have led to numerous technological innovations and have impacted our understanding of the world around us.

Units

• Physics experiments involve measurements that should be accurate and reproducible.

• The base units include:

  • Length (Mechanics)

  • Mass (Mechanics)

  • Time (Mechanics)

  • Temperature difference (Heat)

• Derived units(or compound units) are all other quantities

Derived or Compound Units

• Newton (N) - Force'

  • Unit: \dfrac{kg-m}{s^{2}}

• Joules (J) - Energy

  • Unit: N-m or \dfrac{kg-m^{2}}{s^{2}}

Converting Units

• When converting a large unit into a smaller unit, you move the decimal point to the RIGHT.

• When converting a smaller unit into a larger unit, you move the decimal point to the LEFT.

• Examples:

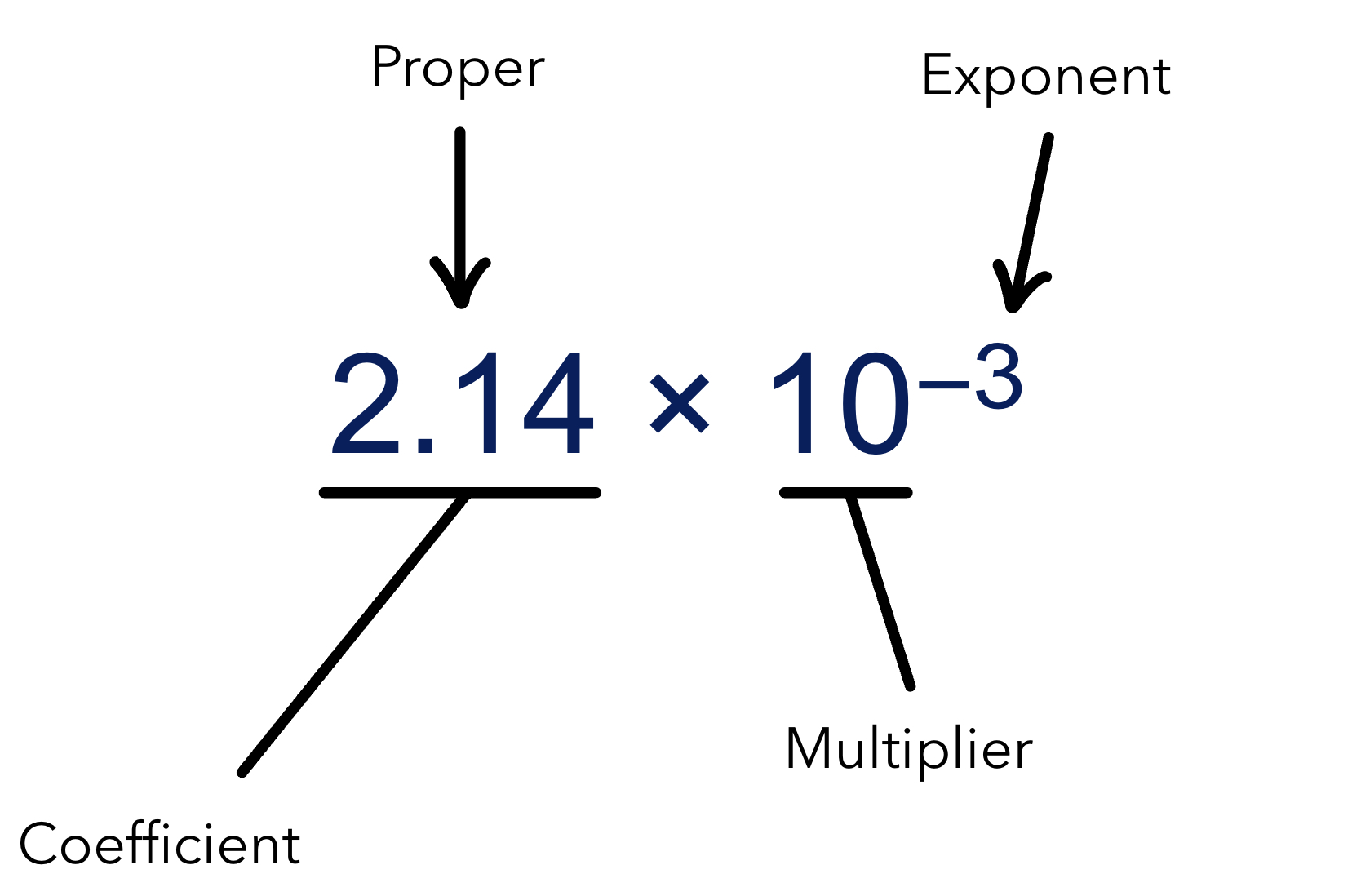
• Example of scientific notation

Significant Figures

• All digits of a measured quantity are called significant figures (SF).

• Rules of significant figures:

  • All non-zeros digits are significant.

    • 2 (2 SF)

    • 453 (3 SF)

    • 8493 (4 SF)

  • Zeros between nonzero digits of a number are significant.

    • 905 (3 SF)

    • 7021 (4 SF)

    • 10,632 (5 SF)

  • Zeros at the end of a number are significant if it contains a decimal point.

    • 450. (3 SF)

    • 12,000,000. (8 SF)

    • 130.0 (4 SF)

  • Zeros at the beginning of a number are NEVER SIGNIFICANT.

    • 0.01 (1 SF)

    • 0.00001 (1 SF)

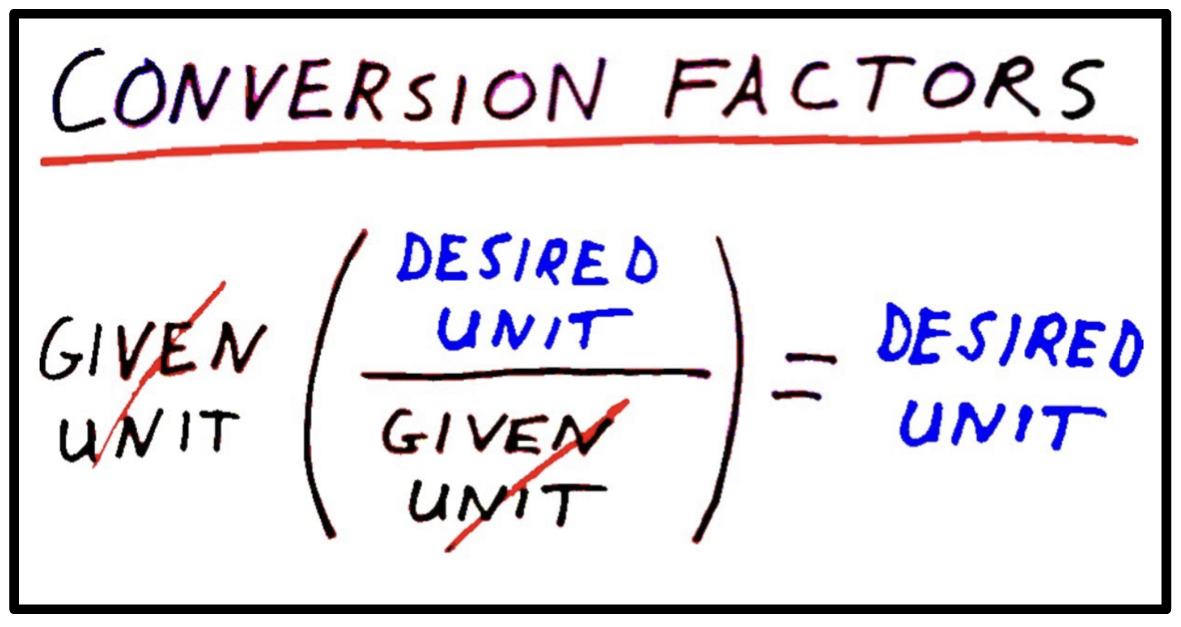
The Role of Units in Problem Solving

• A conversion factor is a fraction that expresses one unit in terms of another that are equivalent to one another.

• Examples of conversion factors include:

  • 1 meter = 100 centimeters

  • 1 foot = 12 inches

  • 1 meter = 39.37 inches

  • 2.54 cm = 1 inch

  • 1 mile = 5280 feet

  • 1 yard = 36 inches = 3 feet

  • 1000 meters = 1 kilometer

• Equation for converting one unit into another:

Dimensional Analysis

1. To add or subtract two things, they must be in the SAME UNIT

2. In any equation, the physical dimensions of each term MUST BE IDENTICAL

Kinetic Energy - Gravitational potential energy. Energy in motion.

• Kinetic energy formula: KE=\dfrac{1}{2}mv^{2}

• Potential energy formula: PE=mgh

Math Review

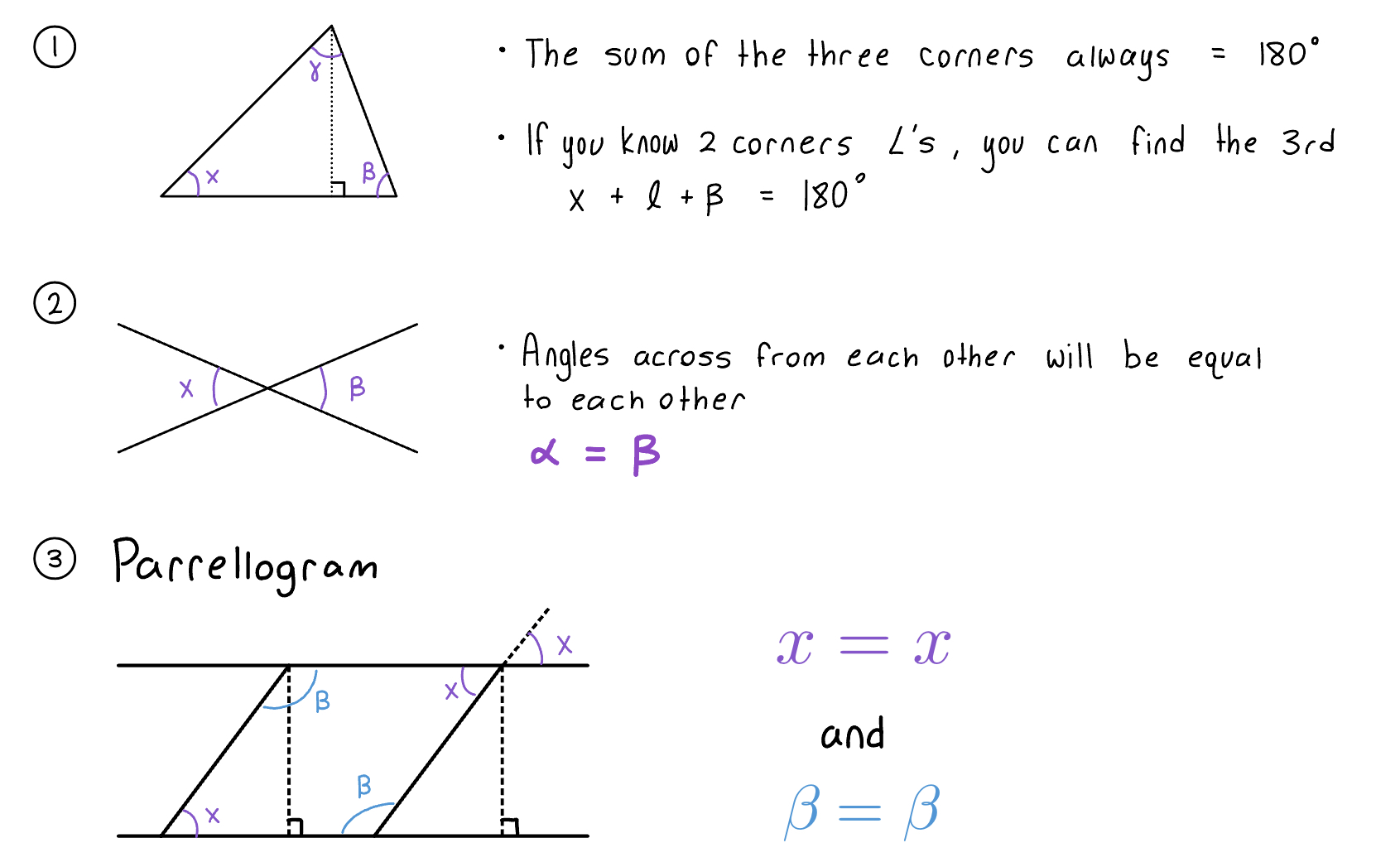
Geometry Review

Trigonometry Review

Scalars and Vectors

• A scalar quantity is one that can be described by a single number.

  • It is a measurement.

  • Examples: temperature, speed, and mass.

• A vector quantity deals inherently with both MAGNITUDE and DIRECTION.

  • Arrows represent them, the direction of the arrow gives the direction of the vector.

  • May point North, South, East, West, East of North, West of South, etc.

  • Examples: velocity, force, and displacement.

Summary Sheet for Vectors

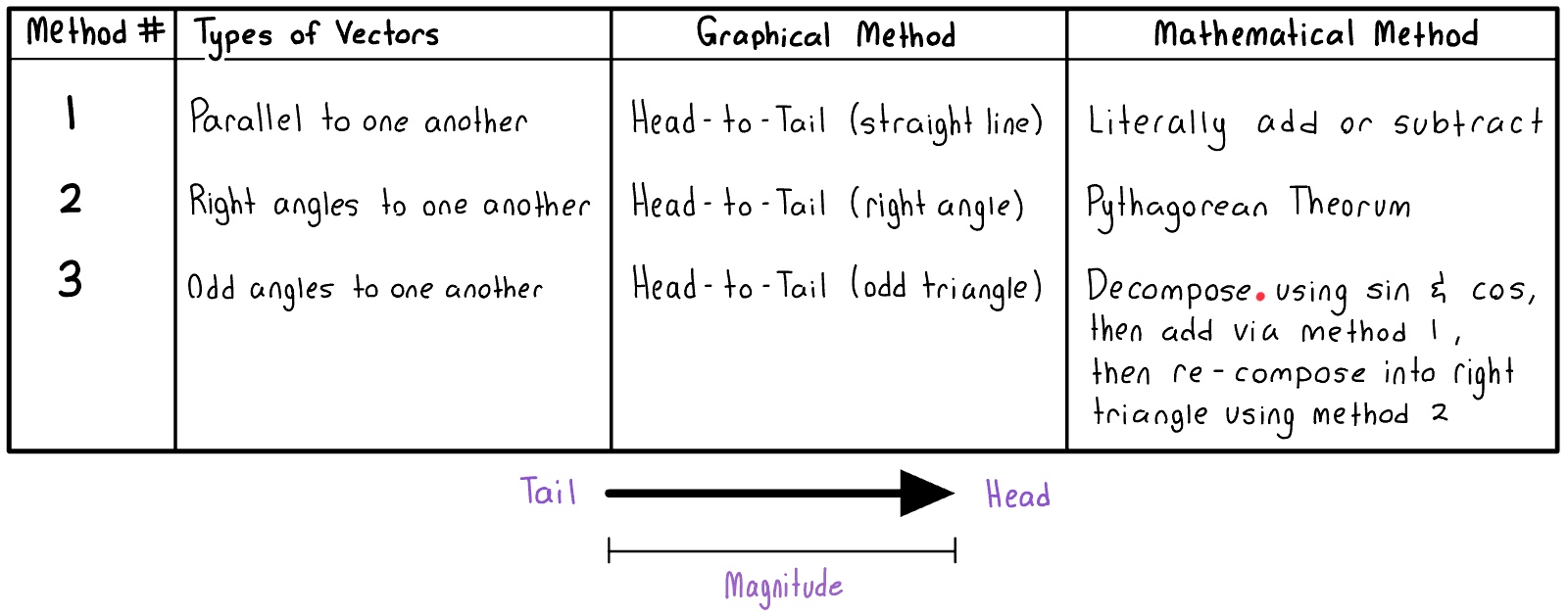
• Equation for Vector Addition: A+B=R

  • A + B represents distance traveled.

  • R represents displacement.

• If it is a triangle, you can use the equation: A^{2}+B^{2}=R^{2}