Characteristics of Gases

• Physical properties of gases are all similar.

• Composed of mainly nonmetallic elements with simple formulas and low molar masses (they’re molecular compounds)

  • Examples of gases:

    • Oxygen (O₂)

    • Nitrogen (N₂)

    • Carbon Dioxide (CO₂)

    • Methane (CH₄)

• Unlike liquids and solids, gases

  • Expand to fill their containers

  • Are highly compressible

  • Have extremely low densities

• Two or more gases form a homogenous mixture.

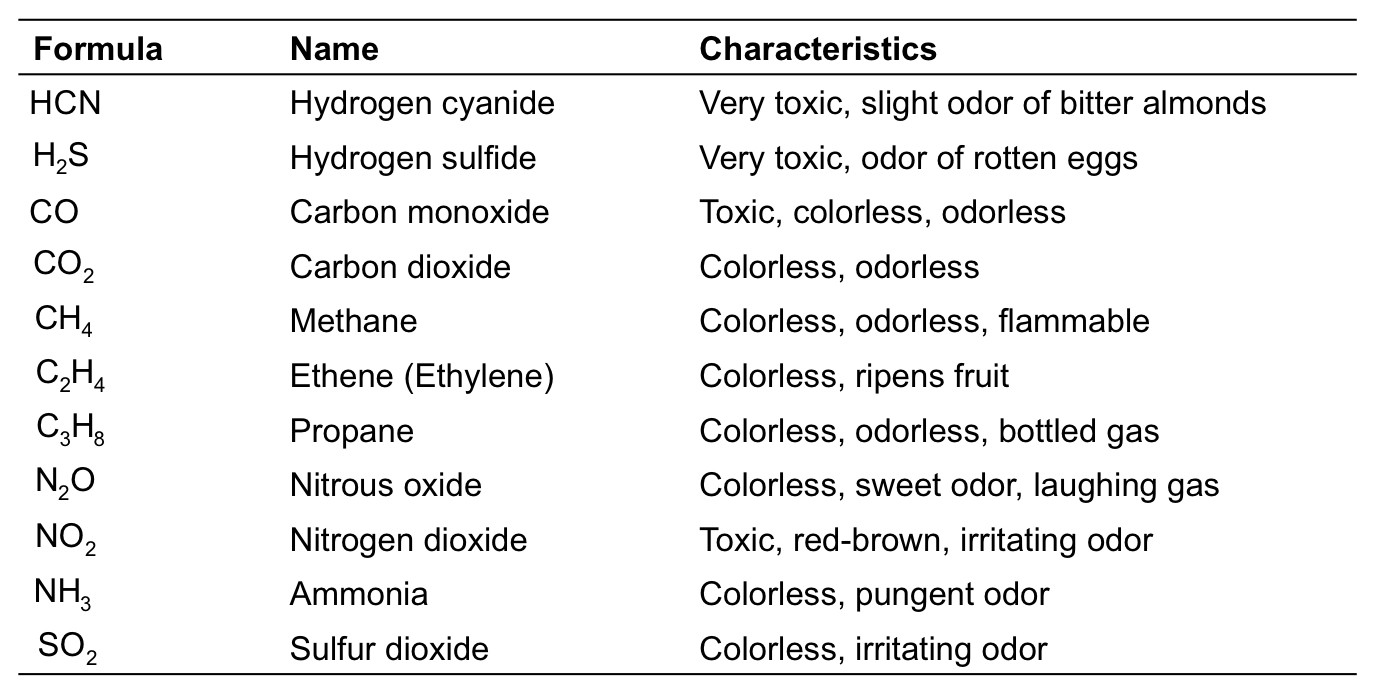
Some Common Gases

Properties That Define the State of a Gas Sample

• Temperature (T)

• Pressure (P)

• Volume (V)

• Amount of gas, usually expressed as number of moles (n)

Pressure

• Pressure is the amount of force applied to an area.

• Pressure formula: P=\dfrac{F}{A}

• Atmospheric pressure is the weight of air per unit of area.

Units of Pressure

• Pascals: 1 Pa = 1 N/m² (SI unit of pressure)

• Bar: 1 bar = 10⁵ Pa = 100 kPa

• mm Hg or torr: These units are literally the difference in the heights measured in millimeters of two connected columns of mercury.

• Atmosphere:

  • 1 atm = 760 torr = 760 mm

  • Hg = 101.325 kPa = 1.10325 bar

Standard Pressure (STP)

• Normal atmospheric pressure at sea level is referred to as standard atmospheric pressure.

• It is equal to

  • 1 atm

  • 760 torr (760 mmHg)

  • 101.325 kPa

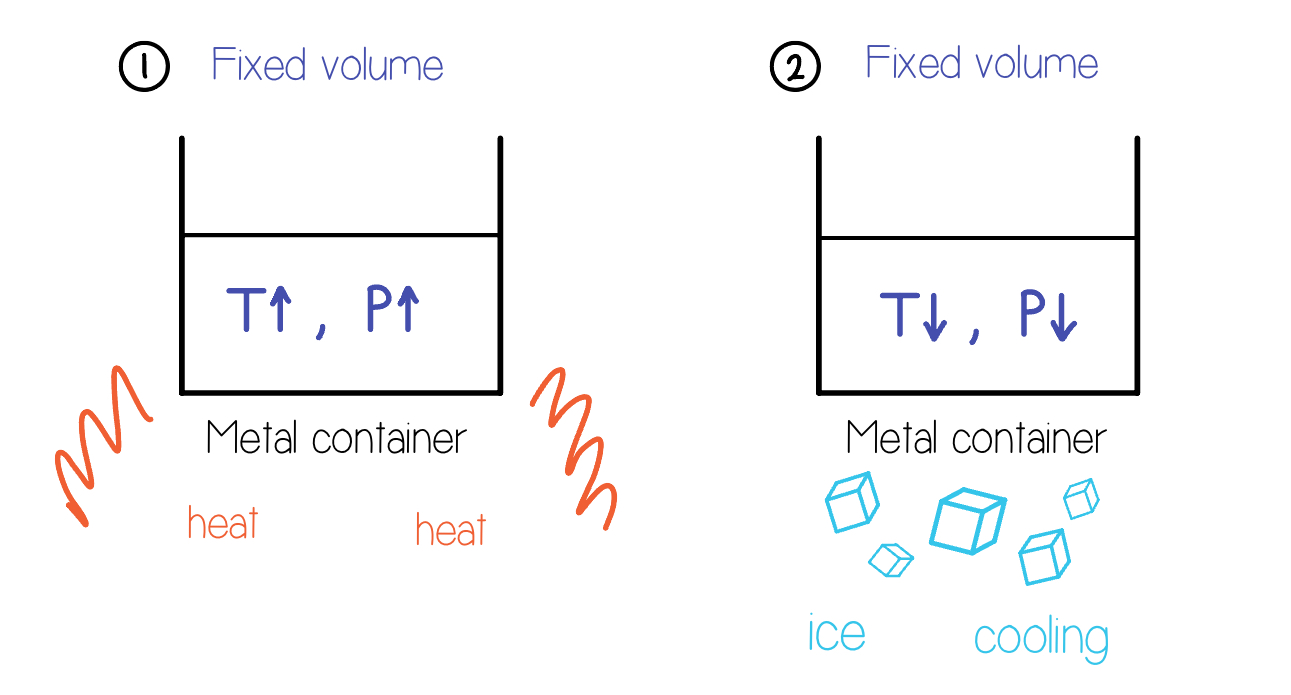
Boyle’s Law

• Boyle’s Law: The volume of a fixed quantity of gas at constant pressure is inversely proportional to the pressure.

• Relationship: inverse

  • When P goes up, V goes down

  • When P goes down, V goes up

• Formula: P_{1}V_{1}=P_{2}V_{2}

Charle’s Law

• Charle’s Law: The volume of a fixed amount of gas at constant pressure is directly proportional to its absolute temperature.

• Relationship: directly proportional

  • When T goes up, V goes up

  • When T goes down, V goes down

• Formula: \dfrac{V_{1}}{T_{1}}=\dfrac{V_{2}}{T_{2}}

Gay-Lussac’s Law

• Gay-Lussac’s Law: At a given temperature and pressure, the volume of gases that react with each other is in small whole numbers.

• Relationship: directly proportional

  • When T goes up, P goes up

  • When T goes down, P goes down

• Formula: \dfrac{P_{1}}{T_{1}}=\dfrac{P_{2}}{T_{2}}

• Example: two volumes of hydrogen gas and one volume of oxygen gas will make two volumes of water vapor.

Combined Gas Law

• This law allows us to calculate the relationship between pressure, volume, and temperature of a gas when the amount of gas is held constant.

• Formula: \dfrac{P_{1}V_{1}}{T_{1}}=\dfrac{P_{2}V_{2}}{T_{2}}

Avogadro’s Law

• Avogadro’s Law: The volume of a gas at constant temperature and pressure is directly proportional to the number of moles of gas.

• So at STP, one mole of ANY gas occupies 22.4 L.

• Formula: \dfrac{V_{1}}{n_{1}}=\dfrac{V_{2}}{n_{2}}

• Set of predetermined T, P, and V values:

  • V = 22.4 L

  • T = 0°C = 273 K

  • P = 1 atm

Ideal-Gas Equation

• Ideal-Gas Law: States that the pressure, volume, and temperature of an ideal gas are related by the equation PV = nRT, where n is the number of moles of gas and R is the ideal gas constant.

Constant R

• The ideal gas constant makes the equation and equality.

• R constant: 0.08206\ \dfrac{L\cdot atm}{mol\cdot K}

Density of Gases

• One needs to know only the molecular mass, the pressure, and the temperature to calculate the density of a gas.

  • Formula: d=\dfrac{MP}{RT}

• If we know the mass, volume, and temperature of a gas, we can find its molar mass.

  • Formula: M=\dfrac{mRT}{PV}

• M = molecular mass

• m = mass

Volume and Chemical Reactions

• Gas laws + Stoichometry

• The balanced equation tells us relative amounts of moles in reaction, whether the compound materials are products or reactants.

Example

Dalton’s Law of Partial Pressure

• If two gases that don’t react are combined in a container, they act as if they are alone in the container.

• The total pressure of a mixture of gases equals the sum of the pressures that each would exert if it were present alone.

• Formula: P_total = P₁ + P₂ + P₃ + …

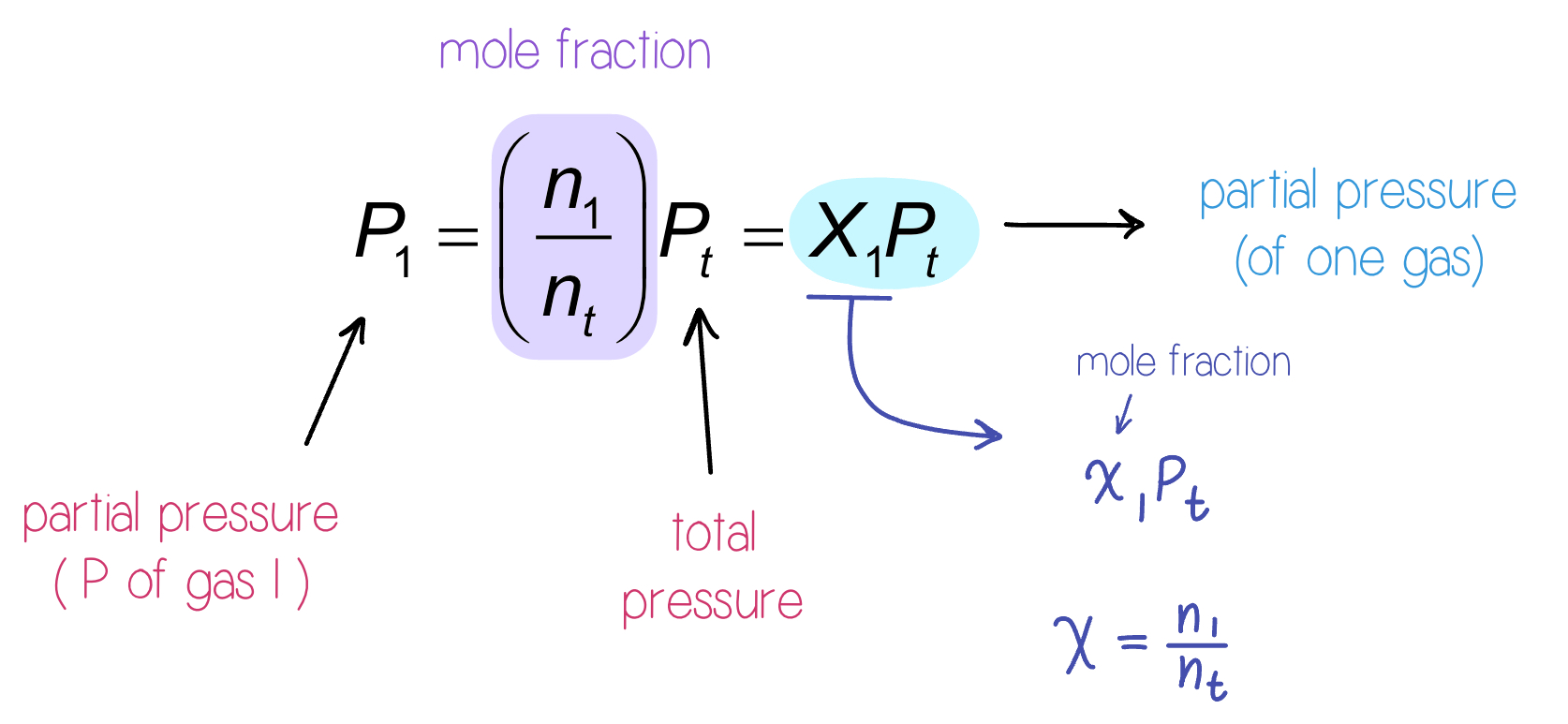
Mole Fraction

• Because each gas in a mixture acts if it is alone, we can relate amount in a mixture to partial pressures.

• That ratio of moles of a substance to total moles is called the mole of fraction,

  • Formula: x_{1}=\dfrac{n_{1}}{n_{t}}

  • Moles of compound 1 \div Total moles

Pressure and Mole Fraction

• The end result is:

Kinetic-Molecular Theory

• Laws tell us what happens in nature.

• Each of the gas laws we have discussed tells us what is observed under certain conditions.

Main Tenets of Kinetic-Molecular Theory

1. Gases consist of large numbers of molecules that are in continuous, random motion.

2. The combined volume of all the molecules of the gas is negligible relative to the total volume in which the gas is contained.

3. Attractive and repulsive forces between gas molecules are negligible.

4. Energy can be transferred between molecules during collisions, but the average kinetic energy of the molecules does not change with time, as long as the temperature of gas remains constant.

5. The average kinetic energy of the molecules is proportional to the absolute temperature.

How Fast Do Gas Molecules Move?

• Temperature is related to the average kinetic.

• Individual molecules can have different speeds.

\mu_rms and Molecular Mass

• At any given temperature, the average kinetic energy of molecules is the same.

• So ½ m (\mu_rms)² is the same for two gases at the same temperature.

• If a gas has a low mass, its speed will be greater than for a heavier molecule.

Effusion and Diffusion

• Effusion is the escape of gas molecules through a tiny hole into an evacuated space.

• Diffusion is the spread of one substance throughout a space or a second substance.

Graham’s Law Describes Diffusion and Effusion

• Graham’s law relates the molar mass of two gases to their rate of speed travel.

• The “lighter” gas always has a faster rate of speed.

• Compares speed of two molecules depending on their mass.

• Formula: \dfrac{r_{1}}{r_{2}}=\sqrt{\dfrac{M_{2}}{M_{1}}}

Real Gases

• The behavior of gases conforms to the ideal-gas equation only at relatively high temperature and low-pressure.

• Even the same gas will show wildly different behavior under high pressure at different temperatures.

Deviations from Ideal Behavior

• The assumptions made in the kinetic molecular model break down at high pressure and/or low temperature.

Corrections for Non-ideal Behavior

• The ideal-gas equation can be adjusted to take these deviations from ideal behavior into account.

• One equation corrected for real gases is known as the van der Waals equation.

• The pressure adjustment is due to the fact that molecules attract and repel each other.

• The volume adjustment is due to the fact that molecules occupy some space on their own.

• van der Waals equation: P = [nRT / (V - nb)] - [a(n/V)^2] ,

  • Where P is the pressure

  • n is the number of moles

  • R is the ideal gas constant

  • T is the temperature

  • V is the volume

  • a is the attraction parameter

  • b is the volume excluded by the gas molecules.

Reference: Chemistry The Central Science (14th Edition)