Integration Methods for AP Calculus AB/BC

Integration is a fundamental concept in calculus, representing the accumulation of quantities and the area under curves. Mastering various integration techniques is crucial for success in AP Calculus. Below is a detailed overview of the key integration methods you should know.

1. Basic Integration Rules

Before diving into advanced techniques, it's essential to know the basic integration rules:

2. Definite Integrals and the Fundamental Theorem of Calculus

The Fundamental Theorem of Calculus connects differentiation and integration:

3. Integration by Substitution

This method is useful for integrals involving composite functions. The steps are:

1. Choose a substitution: Let ( u = g(x) .

2. Differentiate: Find du = g'(x) , dx .

3. Rewrite the integral: Substitute u and du into the integral.

4. Integrate: Solve the integral in terms of u .

5. Back-substitute: Replace u with g(x) .

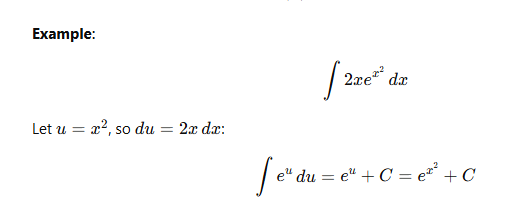
4. Integration by Parts

This technique is based on the product rule for differentiation:

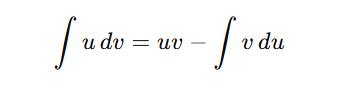
Steps:

1. Choose ( u ) and ( dv ).

2. Differentiate ( u ) to find ( du ).

3. Integrate ( dv ) to find ( v ).

4. Substitute into the integration by parts formula.

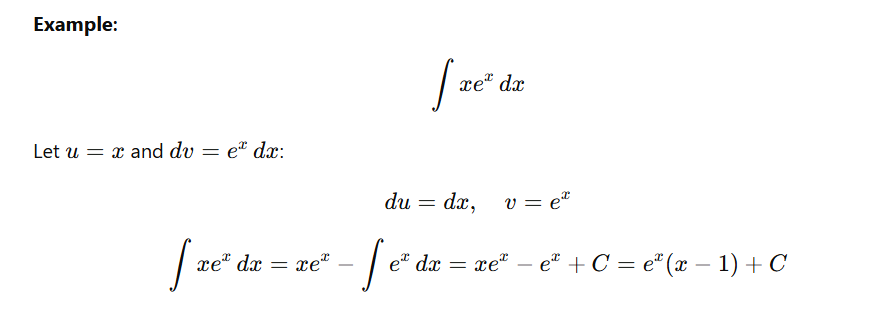
5. Trigonometric Integrals

Integrating powers of trigonometric functions often requires using identities. Common techniques include:

Conclusion

Mastering integration methods is essential for success in AP Calculus AB and BC. The techniques outlined in this review—ranging from basic integration rules to more advanced methods like integration by substitution,