Sampling Concepts and Methods Notes
Context of Sampling in Everyday Communication with Numbers
Research workflow: address a research question or hypothesis
Identify variables: independent vs. dependent
Determine how to measure variables
Plan data collection
Purpose: Statistical inference to answer the research question
Scope: On whom? And how?
Key Concepts: Population, Sample, and Inference
Population: The entire pool from which a statistical sample is drawn
Sample: A subset of the population used for analysis
Sample Frame: A list of all individuals in the population who can be sampled; sometimes not fully attainable
Sampling: A process where a predetermined number of observations are taken from a larger population
Population parameter: A specific value that describes a characteristic of the population (unknown until measured)
Sample statistic: A numerical value calculated from the sample to estimate the population parameter
Statistical inference: Using sample data to make conclusions about the population
Confidence interval: A range of values used to estimate the population parameter
95% confidence interval: A commonly used interval level; interpretation depends on repeated sampling
Interpretation is important: CI conveys uncertainty and reliability of the estimate
Complete Enumeration vs. Sampling
Complete enumeration (studying the population directly)
Strength: Provides a precise answer to the research question
Weakness: Time, energy, and money required
Sampling (studying a subset of the population)
Strength: Saves time, energy, and money
Weakness: Provides an estimate rather than an exact population value
Important generalization: With properly drawn random and representative samples, estimation can be very accurate; otherwise, estimates can be far from the truth
Sampling can be done using probabilistic or non-probabilistic techniques
Probability vs. Non-Probability Sampling
Probability sampling (random sampling)
Every member of the defined population has an equal chance of being selected
Also called unbiased or representative sampling
Requires a sampling frame (at least partially)
Goals: Generalize findings to a broader population; maximize representativeness
Common methods: Simple random, systematic, stratified
Non-probability sampling (non-random sampling)
Does not give all individuals equal chances of selection
Some members are more likely to be included than others
Also called biased or unrepresentative sampling
Often chosen to save resources or when generalization is not the primary goal
Common methods: Volunteer, Convenience, Purposive, Snowball, Quota
Probability Sampling Methods
A probability sampling method uses some form of random selection; every defined population member has an equal chance of being chosen
Requires a sampling frame (or partial frame)
Three main methods:
Simple Random Sampling
Systematic Random Sampling
Stratified Random Sampling
Simple Random Sampling
Basic technique: select a group of subjects from a larger group where every unit has an equal chance of being selected
3 steps:
Get a list of everyone in the population (with identifiers)
Generate appropriate random numbers (e.g., using random number generators)
Select individuals whose identifiers match the random numbers
Systematic Random Sampling
Sample members are selected according to a random starting point and a fixed, periodic interval
Four steps:
Get a list of everyone in the population
Calculate skip interval = Population size/sample size
k = N / n (formula)
k = The skip interval (or sampling interval).
N = The total population size.
n = The desired sample size.
To select a sample, randomly choose a starting point between 1 and k, then select every k-th element from the population until the sample size n is achieved.
Pick a random starting point between 1 and the skip interval
A constant interval is selected to facilitate participant
selection
• 8,18,28,38,48,...This method is known as systematic sampling and is effective for producing a representative sample when the population is ordered.
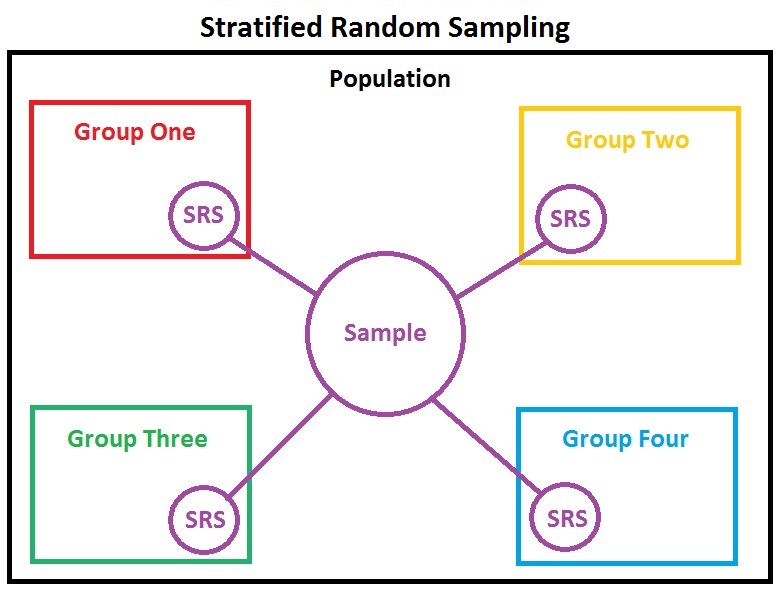
Stratified Random Sampling
Population can be partitioned into subpopulations (strata) of similar units
Within each stratum, apply the same random selection process as simple random sampling
Rationale: ensures representation from each subpopulation
Non-Probability Sampling Methods
Non-probability sampling: samples are gathered in a process that does not give all individuals equal chances of being selected
Five common methods:
Volunteer Sampling
Convenience Sampling
Purposive Sampling
Snowball Sampling
Quota Sampling
Volunteer Sampling
Participants self-select into the study
Often those with a strong interest in the topic
Examples: Research on healing power of prayer; firearms regulation surveys conducted by phone
Convenience Sampling
Also called grab, accidental, opportunity, or haphazard sampling
Sample drawn from the part of the population closest at hand
Example: Interviewing people outside a coffee shop
Purposive (Judgmental) Sampling
Selecting participants based on specific characteristics or study objectives
Nonrandom
Examples: Attending political rallies for interviews; Native Hawaiian family narratives
Snowball (Network) Sampling
Existing subjects recruit future subjects from among their acquaintances
Useful when potential participants are hard to locate
Example: Researching experiences in Alcoholics Anonymous (AA)
Quota Sampling
Assemble a sample that has the same proportions as the population for known characteristics (demographics, etc.)
Similar to stratified sampling but non-random
Example: Studying experiences of different ethnic groups with discrimination
Important note: Non-random selection and no use of a sampling frame
Strengths and Weaknesses of Non-Probability Sampling
Strengths
Save time, energy, and money
Convenient and often feasible
Weaknesses
Not all individuals have equal chances of being selected
Results are not generally generalizable to a broader population
Example: A study based on a sample of UH undergraduates may not generalize to U.S. adults
The sample can be systematically different from the population (bias)
May over- or under-represent certain outcomes
Limited by resources (time, energy, money, etc.) and lack of a sampling frame
Not inherently bad; suitability depends on research objective
Example in practice: Hawaiian Identity through family narratives (topic-sensitive, not necessarily generalizable)
Concrete Example: UH Manoa Sample Scenario
Population (N): 17,490
Sample size (n): 100
Sample gender breakdown: Male 60%, Female 40%
Population gender breakdown: Male 60%, Female 40%
Example numbers: 10,494 males (60%), 6,996 females (40%) in population; 60 males, 40 females in the sample
Purpose of the example: show proportional stratified-like allocation within a simple random framework
Practical Implications and Takeaways
Probability sampling yields representative samples when frames exist and sampling is executed properly
Randomized methods (simple, systematic, stratified) enable generalization and accurate statistical inference if framed correctly
Non-probability methods are valuable for feasibility, exploratory work, or when generalization is not the primary goal
Always consider the objective of the study when choosing a sampling method
Recap and Core Principles
Complete enumeration vs. sampling: trade-off between precision and resources
Probability methods (Simple, Systematic, Stratified): aim for generalizability and representativeness; require frames
Non-probability methods (Volunteer, Convenience, Purposive, Snowball, Quota): resource-efficient; limit generalizability
Key terms to remember: Population, Sample, Sampling Frame, Population Parameter, Sample Statistic, Confidence Interval (e.g., 95%), and the importance of interpretation
Fundamental formulas:
Skip interval in systematic sampling:
Population size/sample sizeSkip interval in systematic sampling: Population size / Sample size; used to determine how many elements to skip in the sampling process. These concepts form the basis for understanding sampling techniques and their application in research.
Practical note: Always align sampling design with research goals, resource constraints, and the level of generalizability required for the study